For a better world

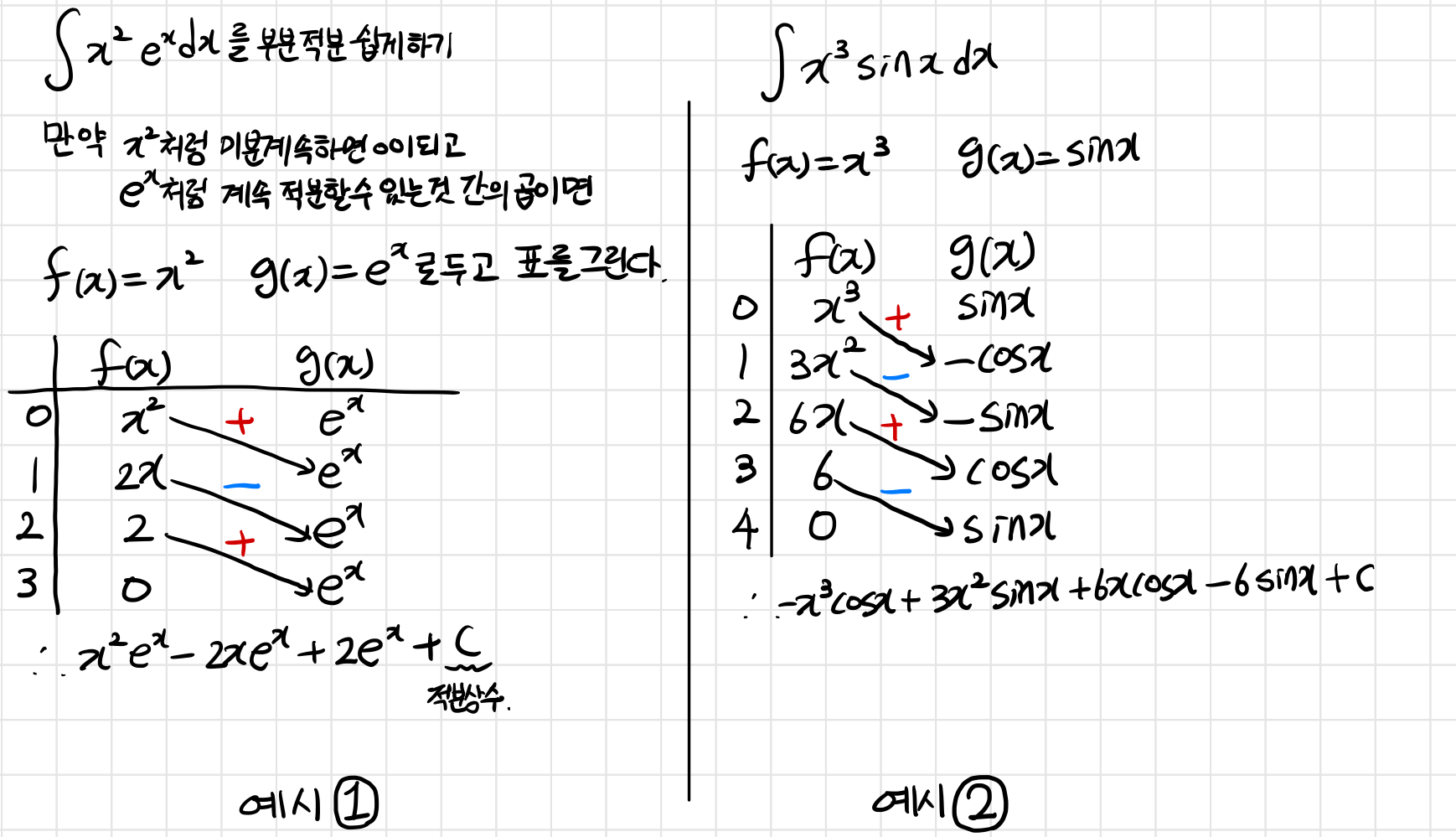
데이터 사이언스 직군으로 면접보며 받았던 질문에 대해 정리 (Last Update: 2022.11.29)

1. Deep Learning

Q1. ReLU의 단점을 설명하라.

ReLU의 경우 Sigmoid의 단점인 gradient vanishing 문제를 극복하기 위해 사용한 활성화 함수입니다.  ReLU의 장점은 입력값을 그대로 출력하기 때문에 구현이 쉽고 빠른 학습이 가능합니다. 반면 단점은 Dead ReLU 현상으로 만약 입력값이 음의 값이 들어온다면 이를 처리하지 못하는 것입니다. 이와 같이 음의 값을 처리하지 못하는 단점을 보완하기 위해 LeakyReLU와 같은 활성화함수를 사용합니다.

Q2. 모델의 일반화 성능을 위해 사용할 수 있는 방법을 설명하라.

모델 일반화 성능 향상을 위해 크게 3가지 관점으로 접근할 수 있습니다. 첫 번째는 데이터 관점, 두 번째는 모델 관점, 세 번째는 하이퍼파라미터 관점입니다. 첫 번째 데이터 관점에서는 학습 데이터셋을 추가하거나 어그멘테이션을 통해 모델 성능을 향상시킬 수 있습니다. 또 학습 데이터셋에 전처리를 통해 더미값과 같은 데이터를 제거해줌으로써 모델 성능을 향상시킬 수 있습니다. 두 번째 모델 관점에서는 트랜스포머 모델을 사용해 RNN 계열 모델의 단점인 long-term dependency와 비병렬성을 극복한 것처럼 더 좋은 모델 아키텍처를 사용하는 방법이 있습니다. 이를 위해 NAS(Neural Architecture Search)와 같은 알고리즘을 사용할 수 있습니다. 또 모델에 오버피팅을 줄이기 위해 BREDLAN이라고하여 Batch Normalization, Regularization, Early Stopping, Dropout, Label Smoothing, Augmentation, Noise Robustness를 적용할 수 있습니다. 마지막 하이퍼파라미터 관점에서는 Random Search나 Grid Search, HyperBand, Keras Tuner등을 통해 손실함수, 학습률, 활성화함수, Optimizer 등의 하이퍼파라미터의 최적값을 찾음으로써 모델의 성능을 향상시키고 일반화할 수 있습니다.

Q3. Word2vec 모델에 대해 설명하라.

word2vec 모델은 2013년에 나온 모델로 기존의 NNLM(Neural Network Language Model)의 단점을 보완하고자 나온 모델이라 할 수 있습니다. 기존 NNLM 모델은 단어를 벡터화시키기 위해 discrete한 방식인 one-hot encoding 방식을 사용했습니다. 하지만 이 방식은 sparse-matrix가 만들어지기 때문에 고차원 상에서 비효율적으로 분산 표상되어 학습이 잘 이루어지지 않습니다. 때문에 이를 continous하게 표상할 수 있도록 만들어진 모델이 word2vec 입니다. word2vec은 내부적으로 학습방식이 CBOW와 Skip-gram으로 나뉩니다. CBOW는 주변단어인 context에 기반해 중심단어를 예측하는 방식이며 Skip-gram은 중심단어에 기반해 주변단어를 예측하는 방식입니다. 두 방식 모두 Input layer, projection layer, output layer 3가지 레이어로 구성되어 동작합니다. 

Q4. CNN의 장점과 단점을 설명하라.

CNN의 장점은 DNN의 단점을 극복한 것입니다. DNN을 통해 3차원인 이미지를 학습한다면 많은 수의 파라미터가 필요하고 오버피팅이 일어나기 쉽습니다. 반면 CNN을 사용하면 DNN에 비해 파라미터 수를 감소시켜 학습이 가능합니다. 또 DNN과 달리 CNN은 이미지의 공간적 형태를 보존합니다. DNN은 이미지의 픽셀간 관계를 고려하지 않고 1차원으로 flatten시키지만 CNN은 픽셀간 관계를 고려할 수 있습니다. CNN의 단점은 풀링 과정에서 정보손실이 발생하는 것입니다. 풀링 과정을 거치면서 정보가 요약됩니다. 이 때 각각의 local feature의 상대적인 위치 정보를 잃을 수 있습니다.

Q4-1 CNN의 동작원리를 설명해라. (예상)

우선 CNN의 구조는 convolution layer와 pooling layer, fully-conncected layer로 구성됩니다. convolution layer를 통해 Input image로부터 feature map을 추출합니다. 추출 과정은 input image에 filter로 슬라이딩 윈도우를 통해 합성곱을 계산하는 방식으로 이루어집니다. 이후 pooling layer를 통해 feature map의 크기를 줄이고 feature를 추출합니다. 최종적으로 flatten 시킨 다음 fully-connected layer에 입력하여 최종 결과를 출력하는 방식으로 동작합니다. 

Q5. RNN의 장점과 단점을 설명하라.

RNN은 시퀀셜 데이터를 처리하기 위해 사용하는 신경망의 한 종류입니다. RNN의 장점은 정의 자체로서 시퀀셜 데이터를 처리할 수 있다는 데 있습니다. 반면 단점은 long-term dependency 문제가 있고 RNN 구조상 병렬처리가 불가능합니다. 이러한 RNN 계열의 단점을 극복하기 위해 Transformer가 고안되었습니다. Transformer는 attention 메커니즘을 사용해 RNN 계열의 단점인 long-term dependency 문제와 비병렬성 문제를 해결했습니다.

Q5-1. RNN의 동작원리를 설명해라. (예상)

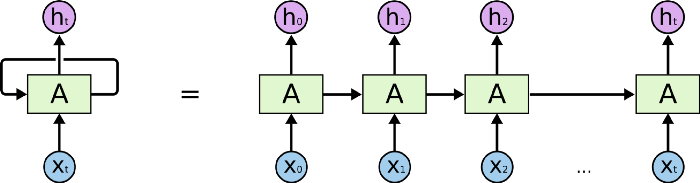
RNN은 크게 Input layer, hidden layer, output layer로 구성되어 있습니다. RNN의 가장 큰 특징은 은닉층이 이전 데이터를 참조하도록 연결되어 있다는 것입니다. 즉 만약 t시점에서 입력 데이터가 들어왔다면 t시점에서 출력하는 것 뿐만 아니라 t+1 시점의 출력에도 영향을 미칩니다. 따라서 시퀀셜한 데이터 처리에 적합하다는 장점이 있습니다. 반면 단점은 long-term dependency 문제가 발생합니다. 가령 오래된 시점에서 입력된 데이터의 영향이 뒤로 갈수록 적어지는 것을 의미합니다. 이러한 문제점을 해결하기 위해서는 LSTM에서 cell state란 개념을 도입해 이를 해결했습니다. 

Q5-2. long-term dependency 문제가 발생하는 이유는 무엇인가요?

핵심은 기울기 폭발과 기울기 소실 문제 때문입니다. RNN은 활성화함수로 tanh를 사용합니다. tanh는 -1과 1사이의 값을 가집니다. 이 때 1보다 작은 값이 반복해서 곱해지기 때문에 feed-forward 관점에선 앞의 정보를 충분한 세기로 전달할 수 없고 back-propagation 관점에서는 tanh 함수의 기울기가 0에 가깝거나 큰 값이 발생할 수 있어 기울기 폭발과 소실 문제가 발생합니다. 참고로 이 때문에 LSTM에서는 기존 RNN 구조에 cell state라는 변수를 추가함으로써 long-term dependency 문제를 해결합니다.

Q5-3. LSTM의 동작원리를 설명해라. (예상)

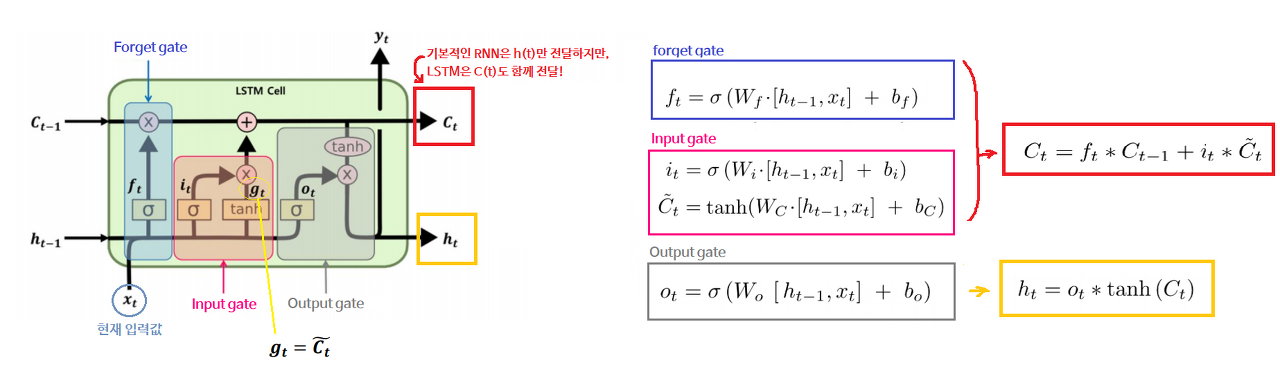
LSTM은 RNN 계열 모델로 RNN의 단점인 long-term dependency 문제를 해결하기 위해 만들어졌습니다. 이 장기의존성 문제를 해결하기 위핸 핵심 개념은 cell-state입니다. LSTM의 구조는 RNN과 유사하지만 내부적으로 게이트가 3개 있습니다. forget gate, input gate, output gate입니다. forget gate에서는 이전의 hidden state와 현재 시점의 Input을 받아 sigmoid 함수를 거쳐 0과 1사이의 값으로 출력합니다. 1이 출력되면 위 cell state의 값과 점곱을 통해 그대로 보내주고 0이 출력되면 cell state의 값이 0으로 초기화 됩니다. 만약 0~1 사이 값이 나오면 일부 정보는 지워진 채 cell state에 업데이트 됩니다. 이후 두 번째 Input gate에서는 sigmoid 함수와 tanh 함수가 있습니다. sigmoid 함수를 거쳐 나온 값과 tanh를 거쳐 나온 값을 점곱을 통해 cell state에 업데이트 해줍니다. 마지막으로 output gate에서는 hidden state 값과 현재 시점의 input값을 마찬가지로 sigmoid 함수를 거친 뒤 tanh함수와 점곱되어 출력됩니다. 그러면 최종적으로 다음 레이어로 넘어갈 cell state가 완성되는 형태입니다. 이러한 LSTM 구조를 사용할 경우 기존의 RNN에서 발생하는 long-term dependency 문제를 해결할 수 있습니다.

Q6. 트랜스포머 구조에 대해 설명하라.

트랜스포머 구조는 크게 인코더와 디코더로 구성이 되어 있습니다. 소스 시퀀스를 인코더에 넣고 압축한 다음 디코더를 통해 타겟 시퀀스를 생성하는 방식으로 동작합니다. 인코더에는 크게 3가지로 MultiHeadAttention 레이어, Poisitionwise FeedForward 레이어, skip connection이 포함된 Layer Normalization 레이어로 구성되어 있습니다. 반면 디코더도 동일하지만 추가적으로 Masked MultiHeadAttention 레이어가 포함되어 있습니다. 트랜스포머의 핵심은 self-attention 메커니즘을 사용한 Query, Key, Value 행렬의 Interaction이라 할 수 있습니다. $Softmax({QK^T \over \sqrt{d_K}})V$로 표현하며 동작 방식은 Query 행렬과 Key 행렬의 전치행렬을 곱해준 다음 smoothing을 위해 $\sqrt{d_K}$ 차원으로 나눠줍니다. 이후 softmax 함수를 취해준 다음 Value 행렬을 곱해주는 방식입니다.

Q7. Adam Optimizer 동작을 설명하라.

먼저 학습은 모델의 예측값과 정답값 사이의 오차를 최소화하는 방향인 Gradient를 구하고 이 방향에 맞춰 모델 전체 파라미터를 업데이트 하는 과정입니다. 이 오차를 최소화 하는 과정을 최적화라고하며 Optimizer는 이 최적화를 위해 사용합니다. 종류는 Stochastic Gradient Descent부터, Momentum, AdaGrad, RMSProp, AdaDelta, Adam, NAdam, Radam, AdamW, AdamP 등이 있습니다. 여기서 Adam이란 Adaptive Moment Estimation을 의미하는 것으로 수리통계학의 적률(모멘트)이란 개념에 기반합니다. (추가 작성 예정)

Adam은 RMSProp과 Momentum 방식을 합쳐 만든 알고리즘입니다. 기울기값의 지수평균과 기울기 제곱값의 지수평균을 활용해 step size를 조절합니다. Adam은 RMSProp과 Momentum 방식을 합쳐 만든 알고리즘입니다. RMSProp와 마찬가지로 기울기 제곱값의 지수 평균을 저장하고, Momentum과 마찬가지로 기울기를 계산했던 것의 지수 평균을 저장합니다.

Q8. GAN에 대해서 설명하라. 

GAN이란 크게 생성자(Generator)와 판별자(Discriminator)로 구성된 모델로 동시에 두 개의 모델을 훈련합니다. 생성자는 최대한 fake 이미지를 만들고 판별자는 최대한 fake 이미지를 탐지하도록 경쟁하는 구조입니다. GAN의 학습목표는 생성자가 생성한 이미지를 판별자가 맞출 확률이 1/2에 수렴하도록하여 진짜 이미지와 가짜 이미지를 구분할 수 없도록 하는 nash equilibrium을 찾는 것입니다. 

Q9. Auto Encoder에 대해 설명하라.

Auto Encoder는 크게 인코더와 디코더의 구조로 구성되어 있습니다. 인코더와 디코더의 중간에 있는 hidden layer는 Input layer보다 적은 수의 뉴런을 두는 bottleneck을 두어 차원을 줄여 압축하고 다시 디코더를 통해 압축된 데이터를 복원시키는 방식으로 동작합니다. 데이터를 압축하는 과정에서 추출한 의미있는 데이터를 보통 latent vector, z로 표현합니다. 즉 Auto Encoder는 학습을 통해 이 latent vector를 자동으로 추출해주는 모델이라 할 수 있습니다. 

Q11. ViT에 대해 설명하라.

ViT는 이미지를 16x16으로 나눠 트랜스포머에 아키텍처에 입력하는 모델입니다. CNN에서 사용하던 필터를 없애고 어텐션으로 대체했습니다. 이미지를 16x16 패치로 나누어 토큰화하여 트랜스포머 아키텍처에 입력합니다. 하지만 트랜스포머는 자연어처리를 위해 만들어진 아키텍처이기 때문에 CNN에 비해 *inductive bias가 부족했기에 기존 CNN을 사용하는 것보다 성능이 떨어졌습니다. 하지만 JFT-300M 데이터셋을 이용해 3억장의 이미지를 학습한 결과 CNN 보다 더 좋은 성능을 얻을 수 있었습니다. 

*inductive bias: 학습시 만나보지 못한 상황에 대해 정확히 예측하기 위해 사용하는 추가적인 가정. 

• CNN은 지역성(Locality)이란 가정을 활용해 공간적(spatial)인 문제를 해결함
• RNN은 순차성(Sequentiality)이란 가정을 활용해 시계열(time-series)인 문제를 해결함

Q12. Diffusion model에 대해 설명하라.

Diffusion model은 generative model 중 하나입니다. 컴퓨터 비전에서 사용됩니다. 데이터에 노이즈를 조금씩 추가해가면서 데이터를 완전한 노이즈로 만드는 forward process가 있고 이와 반대로 노이즈로부터 조금씩 복원해가면서 데이터를 만들어내는 reverse process가 있습니다. (추가 필요)

Q13. Batch Normalization에 대해 설명하라.

Batch Normalization은 activation function의 출력값을 정규화하는 방식입니다. 정규화를 위해 미니 배치마다 평균과 분산을 구해 표준정규분포를 따르도록 만들어주는 방식으로 동작합니다. 이러한 batch normalization이 필요한 이유는 입력 데이터마다 다양한 분포를 갖기 때문에 학습에 있어 모델의 일반화 성능을 가져오기 못하기 때문입니다. 만약 다양한 분포를 가진채로 학습하게 되면 gradient descent에 따른 업데이트 되는 weight에 영향력이 달라지기 때문입니다. 

2. Machine Learning

Q1. 앙상블 기법 종류와 특징에 대해 설명하라.

앙상블 기법은 크게 3가지로 보팅(Voting), 배깅(Bagging), 부스팅(Boosting)이 있습니다. 보팅은 여러 개의 분류기를 통해 최종 예측 결과를 결정합니다. 크게 하드 보팅과 소프트 보팅이 있습니다. 하드 보팅은 분류기의 예측 결과를 다수결 투표를 진행하는 것을 말하고 소프트 보팅은 분류기의 예측 결과의 확률값의 평균 또는 가중합 하는 것을 말합니다. 배깅도 보팅과 마찬가지로 여러 개의 분류기를 통해 나온 예측 결과값을 다수결 투표를 통해 결정하는 것을 말합니다. 차이점이 있다면 보팅은 서로 다른 분류기를 사용하고 배깅은 서로 같은 분류기를 사용해 다수결 투표를 진행하는 것입니다. 배깅의 대표적인 알고리즘은 랜덤 포레스트가 있습니다. 부스팅은 배깅과 비슷합니다. 다만 차이점이 있다면 배깅은 서로 같은 모델들이 독립적으로 학습하여 최종 예측 결과를 내지만 부스팅은 이전 모델의 결과를 기반으로 순차적으로 학습합니다. 가령 첫 번째 모델이 학습한 결과를 기반으로 두 번째 모델이 학습하고 두 번째 모델 결과를 기반으로 세 번째 모델이 학습하는 방식입니다. 이 때 학습 데이터의 샘플 가중치가 계속해서 조절되는 것이 특징입니다. 이러한 부스팅은 오답에 대해 높은 가중치가 부여될 수 있어 outlier에 취약하단 단점이 있습니다. 이러한 부스팅에는 XGBoost나, AdaBoost, GradientBoost과 같은 종류의 알고리즘이 있습니다.

Q2. 랜덤 포레스트에 대해 설명하라. (예상)

랜덤 포레스트는 앙상블 기법 종류 중 배깅 방식에 속하는 알고리즘입니다. 배깅 방식의 특징은 부트스트래핑을 통해 데이터를 랜덤 샘플링하는 과정이 있습니다. 랜덤 포레스트는 다수의 의사결정트리를 만들고 각각의 트리에서 랜덤 샘플링된 데이터를 학습한 다음 최종 예측 결과를 투표하는 방식으로 동작합니다. 또 랜덤 포레스트는 단일한 의사결정트리를 사용했을 때 오버피팅될 수 있다는 단점을 극복하기 위해 만들어진 것이기에 오버피팅을 감소시켜주고 비교적 일반화된 성능을 낼 수 있다는 장점이 있습니다.

Q3. XGBoost와 LightGBM에 대해 설명하라. (예상)

XGBoost와 LightGBM은 모두 앙상블 기법 종류 중 부스팅 방식에 해당하는 알고리즘입니다. 공통적으로 Gradient Boosting Machine에 기반한 방식입니다. XGBoost는 GBM의 3가지 단점을 개선했습니다. 첫 번째로 GBM은 병렬처리가 되지 않아 속도가 느렸다는 한계가 있었고 이를 해결하여 병렬처리를 통해 수행 속도를 빠르게 했습니다. 두 번째는 GBM에 Regularization 기능이 없어 오버피팅이 발생할 수 있단 한계가 있었지만 XGBoost는 자체적으로 Regularization 기능을 포함하고 있습니다. 세 번째로 Early Stopping 기능이 있다는 장점이 있습니다. Decision Tree 기반 알고리즘 중 성능이 우수하다고 알려져 있어 Kaggle과 같은 곳에서 많이 사용되고 있습니다. LightGBM은 XGBoost가 만들어지고 2년뒤에 만들어진 부스팅 알고리즘입니다. XGBoost가 GBM에 비해 빠르지만 여전히 학습 시간이 오래걸린다는 단점이 있습니다. 때문에 LightGBM은 이러한 XGBoost의 느린 학습 시간이라는 단점을 보완했고 또 메모리 효율성을 가져온 알고리즘입니다.

Q4. Gradient Descent에 대해 설명하라.

Gradient Descent는 cost function의 값이 최소가 되게 하는 가중치를 찾는 알고리즘입니다. 신경망에서 back-propagation을 위해 사용되며 cost function을 미분한 다음 learning rate를 곱해주고 체인룰을 적용해 앞단에 위치한 레이어의 가중치를 업데이트 하는 방식으로 동작합니다. 이 Gradient Descent 방식은 전체 데이터를 사용해 기울기를 계산하기 때문에 학습에 많은 시간이 필요하단 단점이 있습니다. 때문에 이런 단점을 보완하기 위해 미니 배치 사이즈로 나누어 학습을 진행하는 Mini-Batch Stochastic Gradient Descent 방식이 사용되기도 합니다.

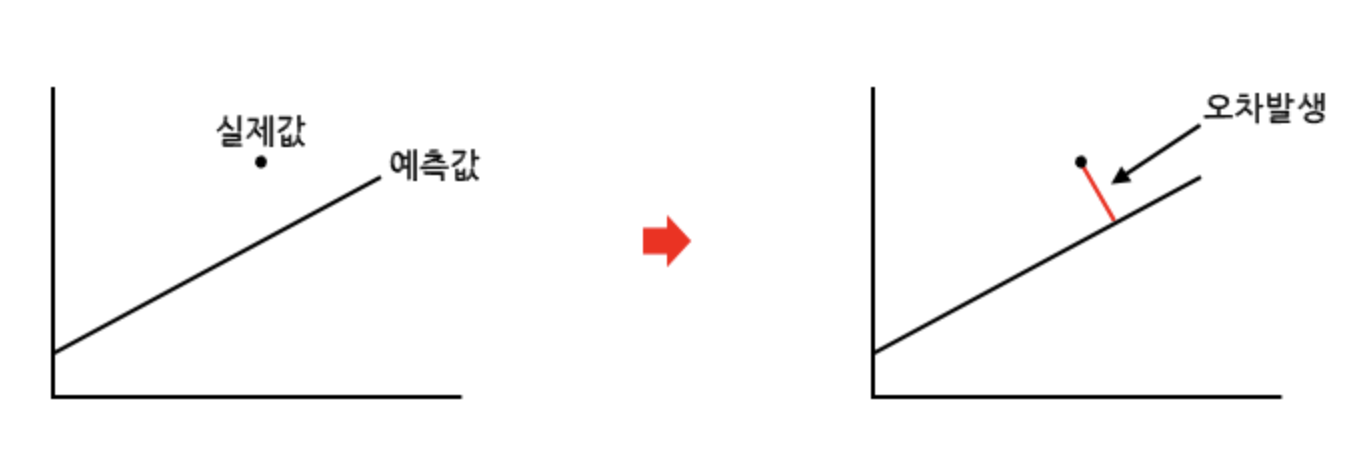
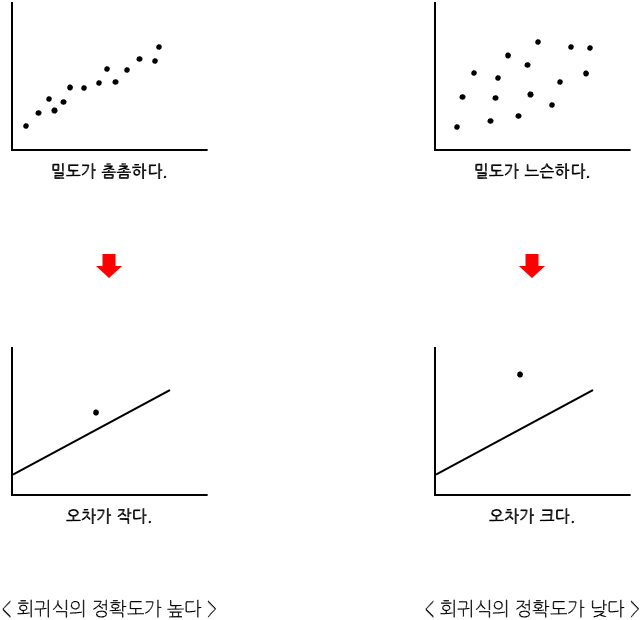
Q5. Bias-Variance Trade-off에 대해 설명해주세요. (예상)

Bias는 under-fitting과 관련 있는 것으로 모든 데이터를 고려하지 못해 지속적으로 잘못된 것을 학습하는 경향입니다. 만약 Bias가 높으면 예측과 정답의 차이가 크게 벌어진 상황을 의미하고 Bias가 낮다면 예측과 정답이 차이가 작은 상황을 의미합니다. 반면 Variance는 over-fitting과 관련 있는 것으로 데이터 내에 노이즈까지 잘 잡아내어 실제 정답과 관련 없는 random한 것 까지 학습하는 경향을 의미합니다. variance가 높다는 것은 예측값과 정답값 간의 범위가 멀다는 것을 의미하고 variance가 낮다는 것은 예측값과 정답값 간의 범위가 좁다는 것을 의미합니다.

Q6. Training, Validation, Testing 셋으로 나누는 이유에 대해 설명하라. (예상)

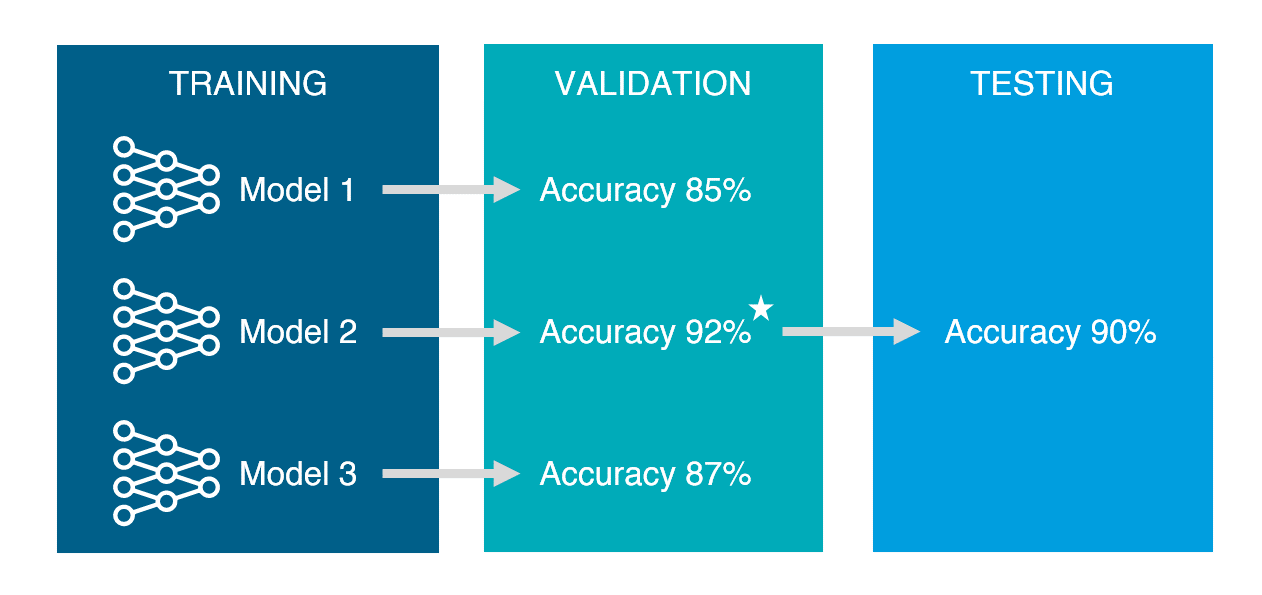
먼저 Training set은 모델 학습을 목적으로 사용합니다. 만약 training set을 평가에 사용한다면 이미 한 번 본 시험으로 재시험을 보는 것과 같기에 별도의 validation set이나 testing set으로 나누어 주어야 합니다. 이후 validation set의 경우 training set으로 만든 모델의 성능을 측정하기 위해 사용합니다. 이를 위해 다양한 모델과 파라미터를 사용해가며 validation set에 적합한 모델을 선택해야 합니다. 이후 마지막으로 testing set을 이용해 단 한번 모델의 성능을 측정하기 위해 사용합니다. 이후 training set, validation set, testing set을 모두 합쳐 다시 모델을 학습하여 최종 모델을 만듭니다. 간단한 비유를 하자면 training set은 월별 모의고사고 validation set은 그 중에서도 9월 모의고사처럼 실제와 비슷할 것이라 판단되는 모의고사이며 마지막 testing set을 통해 수능을 보는 것과 같습니다. 

Q7. K-fold cross validation에 대해 설명하라. (예상)

K-fold cross validation이란 전체 데이터에서 training set과 validation set을 번갈아가며 나누는 방법을 의미합니다. 예를 들어 전체 데이터를 5분할을 한다면 처음엔 가장 첫 번째 분할을 validation set으로 두고 나머지 네 개의 분할을 training set으로 두고 두 번째 학습에는 두 번째 분할을 validation set으로 두고 나머지 분할을 training set으로 두는 것과 같습니다. 이렇 게 하는 이유는 데이터셋의 크기가 작을 경우 validation set에 대한 성능평가 신뢰성이 떨어지기 때문입니다. 즉 특정 validation set에만 적합한 모델을 피하고 전체 데이터셋에 균형 잡힌 학습을 위해 사용합니다.

3. Probability/Statistics

Q1. Posterior, Prior, Likelihood에 대해 설명하라.

이 세 개의 개념은 베이즈 정리에 사용됩니다. 베이즈 정리란 Prior, Likelihood, Evidence를 통해 Posterior를 예측하는 방법입니다. Prior는 사전에 이미 알고 있는 확률을 뜻하고 Posterior는 새로 추정된 확률을 뜻합니다. Likelihood는 Probability와 대조적인 특징이 있습니다. Probability는 확률분포를 이미 알고 있다는 가정하에 확률변수값이 계산됩니다. 반면 Likelihood는 확률과달리 확률분포를 모른다는 가정하에 주어진 관측을 통해 확률분포를 추정해나가는 방식입니다. Probability는 특정 사건 발생확률을 더하면 1이될 수 있지만 Likelihood는 그렇지 않습니다. 즉 요약하면 사전확률과 가능도와 새로 관측된 데이터를 통해 사후확률을 계산하는 것이 베이즈 정리입니다. 이 베이즈 정리는 조건부 확률에 기반하며 손쉽게 유도가능합니다.

Q1-1. 베이즈 정리 예시를 설명해라.

Q2. Hidden Markov Chain에 대해 설명하라.

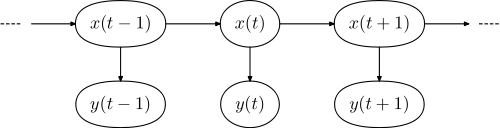
히든 마르코프 체인의 경우 마르코프 체인을 기반으로 합니다. 마르코프 체인이란 마르코프 성질을 가진 이산확률과정입니다. 마르코프 성질이란 미래 상태는 현재 상태에 의해 결정되는 성질입니다. 즉 인과성이 있다는 것입니다. 또 이산확률과정이란 시간의 흐름에 따라 확률적인 변화를 가지는 구조를 의미합니다. 마르코프 성질의 대표적인 예시로는 날씨 예측이 있고 아닌 예시로는 매 번 독립 시행인 동전던지기가 있습니다. 히든 마르코프 체인의 경우 이러한 마르코프 체인에서 확장된 것으로 시스템이 은닉 상태와 관찰 가능한 결과 두 가지의 요소로 이뤄진 모델입니다. 관찰 가능한 결과는 은닉 상태에 의해 결정되지만 은닉 상태는 직접적으로 볼 수 없습니다. 오로지 마르코프 과정을 통해 도출된 결과만 관찰할 수 있습니다. 이런 히든 마르코프 체인은 주로 시퀀셜한 데이터를 다루는데 강점이 있습니다.

Q3. Entropy, Cross entropy, KL-divergence에 대해 설명하라.

entropy는 불확실성을 뜻하는 것으로 확률분포에서 확률변수 X의 기대값을 의미합니다. 수식으로는 $\displaystyle H(x) = -\sum_{i=1}^n p(x_i)\log p(x_i)$로 정의할 수 있습니다. cross entropy 같은 경우엔 entropy가 단일 확률분포에서 어떤 확률변수가 나타날 불확실성이었으면 cross entropy는 두 확률분포 간의 차이를 나타내는 척도라고 할 수 있습니다. 수식으로는 $\displaystyle H_{p, q}(x) = -\sum_{i=1}^n p(x_i)\log q(x_i)$로 나타냅니다. 마지막으로 KL-divergence는 두 확률분포 간의 차이를 나타내는 척도입니다. cross-entropy에서 entropy를 뺀 값이며, 수식으로는 $\displaystyle KL(p||q) = \sum_{i=1}^n p(x) \log {p(x)\over q(x)}$로 나타냅니다. 사실상 cross entropy와 거의 동일해 KL-divergence를 최소화 하는 것은 cross entropy를 최소화 하는 것과 같습니다. 하지만 KL-divergence에 있는 $p(x)\log p(x)$는 모델이 예측하고자 하는 실제 모집단분포이므로 바뀌지 않고 알 수 없는 값입니다. 따라서 cost function으로 사용하려면 상수 취급되어 계산에 포함하지 않아야 합니다. 그러면 남는 것은 $\displaystyle -\sum_{i=1}^n p(x_i) \log q(x_i)$이고 이는 곧 cross entropy를 의미합니다.

Q4. 정규분포에 대해 설명해주세요. (예상)

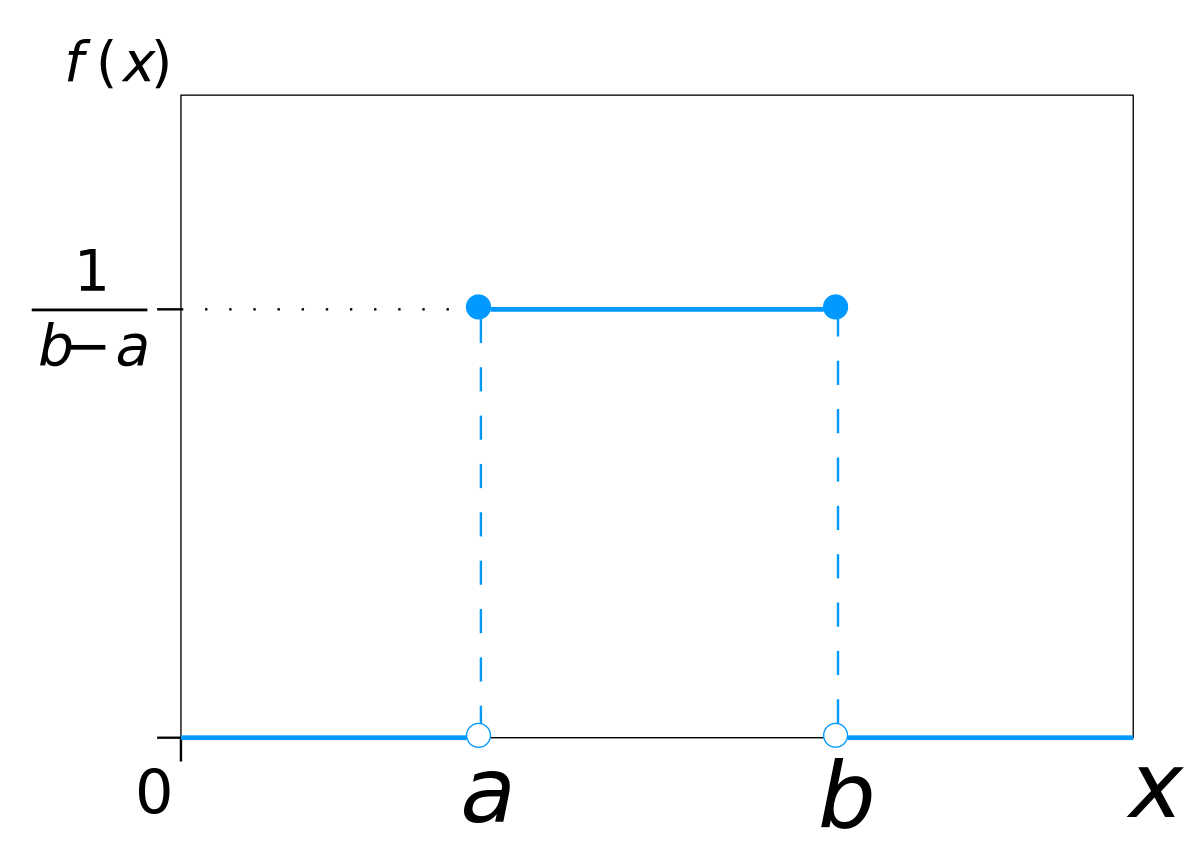
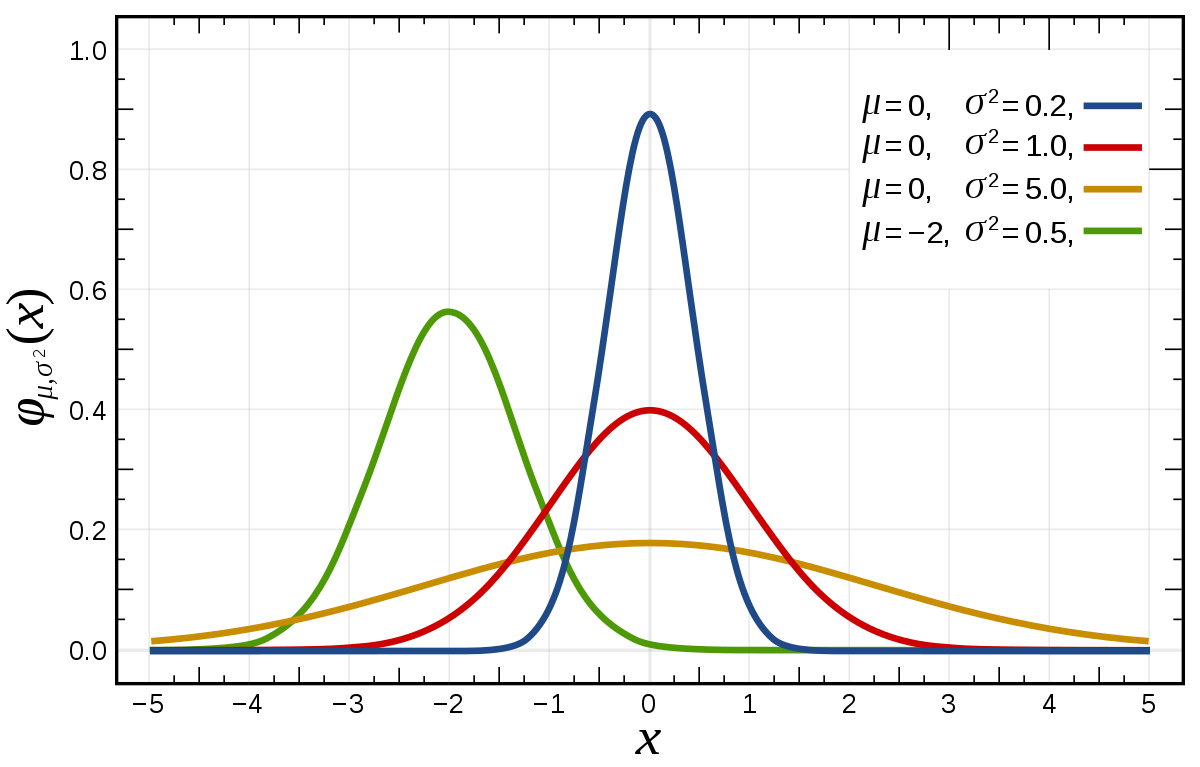
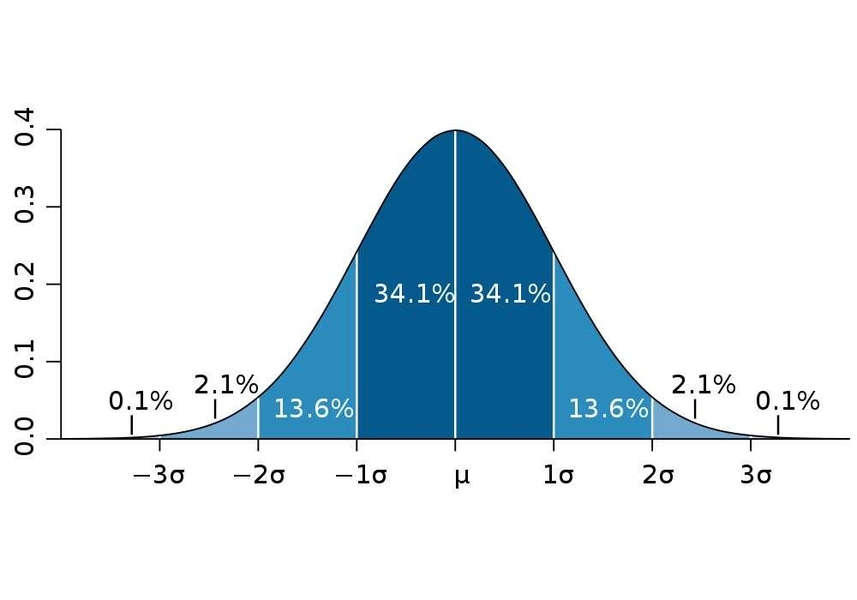
정규분포는 여러 확률분포함수 중에서 연속확률분포에 속하는 분포입니다. 수식은 $\displaystyle f(x) = {1 \over \sqrt{2\sigma^2}} \exp (- {(x-\mu)^2 \over 2\sigma^2})$로 나타냅니다. 이 정규분포는 평균과 분산 값에 따라 다양한 정규분포를 갖게 됩니다. 그 중 평균이 0, 분산이 1인 정규분포를 표준정규분포라 합니다. 이런 정규분포의 특징은 평균을 기준으로 대칭성을 띤다는 것입니다. 따라서 평균 기준 왼쪽과 오른쪽은 각각 0.5의 확률을 같습니다. 또 정규분포별 평균과 분산이 다르더라도 표준편차 구간 별 확률은 어느 정규분포에서나 같다는 것입니다. 

Q5. 이항분포에 대해 설명해주세요. (예상)

이항분포는 베르누이 시행을 n번 시행한 것 입니다. 어떤 사건 A가 발생할 확률이 p일 때 베르누이 시행을 n번 시행한다면 사건 A가 몇번 발생하는지를 확률변수로 두는 분포입니다. 수식으로는 $\displaystyle {}_n C{}_r p^r (1-p)^{n-r}$로 표현합니다. 평균 $E(x)$는 $np$입니다. 또 분산 $V(x)$는 $np(1-p)$입니다. 가장 흔한 예시로는 주사위를 n번 던졌을 때 특정 숫자가 나올 확률이 어떻게 되는가를 구할 때 사용합니다. 특정 숫자가 나올 확률은 ${1 \over 6}$ 이므로 $\displaystyle {}_n C {}_r {1\over 6}^r {5\over 6}^{n-r}$로 나타낼 수 있습니다. 

Q5. 균등분포의 역함수로 샘플링하는 샘플링 기법은 무엇인가? (Box-Muller Transformation에 대해 설명하라)

Q6. 공분산 행렬과 상관 계수에 대해 설명해주세요.

4. Reinforce Learning

Q1. 벨만 방정식에 대해 설명하라.

벨만 기대 방정식은 강화학습에 사용됩니다. 벨만 기대 방정식은 현재 상태의 가치함수와 다음 상태의 가치함수 사이의 관계를 나타낸 식입니다. 여기서 가치함수란 에이전트가 다음 상태로 갈 경우 앞으로 받을 전체 보상에 대한 기대값입니다. 가치함수는 현재 에이전트의 정책에 의해 영향을 받는데, 이 정책을 반영한 식이 벨만 기대 방정식이라 합니다. 정의상 기대값을 알려면 모든 보상에 대해 고려해야하지만 물리적으로 불가능 하므로 하나의 변수를 두고 그 변수를 계속해서 업데이트하는 과정으로 계산됩니다. (추가 필요)

Q2. DQN에 대해 설명하라. 또 DQN의 수식의 의미를 설명하라.

5. Computer Science

Q0. 프로세스와 쓰레드의 차이는 무엇인가?

Q0. 쓰레드의 특징은 무엇인가?

Q1. 캐시는 왜 사용하는가?

캐시를 사용하는 핵심 이유는 CPU 처리속도와 메모리 처리속도 차이에서 발생하는 병목현상을 해결하기 위해 사용합니다. 주기억장치인 메모리에 있는 데이터에 접근하는 시간을 줄이기 위해 CPU와 메모리 사이에 캐시 메모리를 둡니다. 캐시 메모리에는 주기억장치 내에서 자주 읽고 쓰는 데이터의 일부를 캐시 메모리에 불러와 속도 차이를 줄입니다. 그리고 캐시 메모리에는 적중률이라는 개념이 있습니다. CPU가 메모리에 접근하기 전에 캐시 메모리에 먼저 원하는 데이터가 존재하는지 여부를 확인하는데 이 때 있다면 적중한 것이고 없다면 실패한 것입니다. 캐시 메모리를 효율적으로 활용하기 위해서는 적중률이 높아야하고 이를 위해 지역성이라는 개념을 사용합니다. 크게 시간적 지역성, 공간적 지역성, 순차적 지역성 세 가지가 있습니다. 시간적 지역성은 최근 액세스된 메모리 영역은 근 미래에 다시 액세스할 가능성이 높다는 것을 뜻하고, 공간적 지역성은 CPU가 참조한 데이터와 인접한 영역에 있는 데이터 역시 참조될 가능성이 높음을 의미합니다. 마지막으로 순차적 지역성은 메모리에 데이터가 저장된 순서대로 이용될 가능성이 높다는 것입니다. 

Q2. vCPU란 무엇인가?

클라우드 환경에서 만들어지는 가상화 머신에 할당되는 형태의 CPU를 말합니다. 실제 물리적인 CPU 코어를 논리적으로 분할하여 가상화 머신에 할당하는 형태입니다.

Q3. HDD, SSD, DRAM의 차이는 무엇인가? 

핵심 차이는 속도라고 할 수 있습니다. DRAM이 가장 빠르고 SSD가 그다음 HDD가 마지막입니다. DRAM은 Dynamic Random Access Memory로서 RAM의 한 종류입니다. 이외의 종류는 Static Random Access Memory인 SRAM이 있습니다. SRAM은 속도가 빨라 캐시로 사용되고 DRAM은 속도가 상대적으로 느린 대신 용량이 크다는 특징이 있습니다. SSD Solid State Drive의 약자로 비휘발성 저장장치 입니다. 물리적으로 데이터가 위치하는 원판까지 플래터를 이동시켜야하는 HDD와 달리 전자적으로 정보를 읽고 쓰기 때문에 속도가 빠르다는 장점이 있습니다. 

Q4. 가상 메모리를 왜 사용 하는가?

가상 메모리를 사용하는 핵심 이유는 과거 메모리 용량의 한계가 있던 때, 메모리 크기보다 큰 프로세스를 실행시키기 위한 방법이 필요했습니다. 때문에 이를 해결하고자 디스크에서 프로세스 실행에 필요한 부분만 메모리에 적재하고 실행시킬 수 있도록 한 것입니다. 이 가상 메모리를 구현하기 위해서는 MMU라는 Memory Management Unit이 필요합니다. MMU는 가상 메모리에 사용되는 가상 주소를 실제 물리 주소로 매핑해주는 역할을 합니다. 이 때 모든 가상 주소를 물리 주소로 바꾸려면 많은 부하가 생길 수 있으므로 메모리를 페이지라는 단위로 나누어 효율적으로 처리합니다. 

Q5. 페이지 폴트란 무엇입니까? (예상)

페이지 폴트란 CPU가 프로세스 실행에 필요한 단위인 페이지를 요청 할 때 그 페이지가 실제로 메모리에 적재되어 있지 않을때 발생하는 인터럽트입니다. 만약 페이지 폴트가 발생하면 운영체제는 필요로 하는 페이지를 메모리로 가져와서 실행함으로써 마치 페이지 폴트가 발생하지 않은 것처럼 합니다. 이 때 페이지 폴트가 자주 일어나면 오버헤드로 인해 컴퓨터 성능이 저하될 수 있으므로 페이지 폴트를 최소화하기 위해 여러 페이지 교체 알고리즘을 사용합니다. 

Q6. 스래싱(Trashing)에 대해 설명하라. (예상)

쓰래싱은 어떤 프로세스에 지속적으로 페이지 폴트가 발생하는 현상을 의미합니다. 달리 말해 페이지 폴트율이 높아져 프로세스 처리시간보다 페이지 교체시간이 더 많이 발생하는 현상입니다. 이러한 스래싱 현상을 해결하기 위해 크게 두 가지로 Page-Fault Frequency(PFF)와 워킹셋(Working Set)을 사용합니다. 먼저 페이지 폴트율을 주기적으로 계산해서 각 프로세스에 할당할 메모리 양을 동적으로 조절합니다. 만약 어떤 threshold를 넘으면 프로세스에 할당된 프레임이 부족하다 판단하고 프로세스에게 프레임을 추가로 할당합니다. 만약 할당할 빈 프레임이 없을 경우 일부 프로세스를 스왑아웃 시켜 할당합니다. 반면 어떤 threshold이하일 경우 프로세스에게 많은 프레임이 할당된 것으로 판단해 할당된 프레임의 수를 줄입니다. 만약 모든 프로세스에 필요한 프레임을 다 할당한 뒤에도 여유 공간이 있다면 스왑 아웃되어 있던 프로세스를 스왑 인하여 다중프로그래밍정도인 MPD를 높입니다. 

워킹셋은 프로세스가 실행되기 위해 한 번에 메모리에 올라와있어야 할 페이지의 집합을 의미합니다. 워킹셋 알고리즘을 통해 이러한 페이지 집합을 결정할 수 있습니다. 또 프로세스의 워킹셋이 한 번에 메모리에 올라갈 수 있는 경우에만 프로세스에게 메모리를 할당합니다. 그렇지 않은 경우 프로세스에게 할당된 페이지 프레임을 모두 반납하구 프로세스 주소 공간 전체를 디스크로 스왑 아웃시킵니다.

Q7. 페이지 스와핑에 대해 설명해주세요. (예상)

페이지 스와핑은 중기 스케쥴러에 의해 처리됩니다. 페이지 스와핑은 크게 페이지 스왑 인과 페이지 스왑 아웃으로 나뉩니다. 페이지 스왑 인의 경우 프로세스가 실행될 때 페이지 폴트가 발생할 경우 페이지를 메모리에 추가 적재하기 위해 사용합니다. 반면 페이지 스왑 아웃의 경우 워킹셋 알고리즘이 동작할 때 처럼 특정 페이지셋이 한 번에 메모리에 적재되기에 공간이 충분하지 않을 때 디스크 영역으로 옮기는 것을 말합니다.

Q8. 페이지 교체 알고리즘에 대해 설명하라.

페이지 교체는 메모리에 적재할 공간이 부족할 때 메모리에 적재된 프로세스를 디스크로 스왑 아웃하고 프로세스 실행에 필요로 하는 페이지를 메모리에 적재하는 것입니다. 이러한 페이지 교체 알고리즘의 목표는 Page-Fault Frequency를 최소화하는 것입니다. 이런 알고리즘의 종류는 FIFO, LRU, LFU, 빌레디, 클럭등이 있습니다. (추가 설명 필요)

Q9. 페이징의 장단점은 무엇인가?

페이징은 외부 단편화 문제를 해결하기 위해 사용하는 메모리 관리 기법입니다. 외부 단편화는 여분의 메모리 공간이 요청한 메모리 공간보다 커서 여유가 있지만 여유 공간이 연속적이지 않아 발생하는 현상입니다. 페이징은 페이지라는 단위로 메모리 공간에 불연속적으로도 적재할 수 있도록 합니다. 이처럼 페이징을 이용하면 외부 단편화 문제를 해결하는 장점이 있지만 반면 내부 단편화 문제가 발생하는 단점이 있습니다. 내부 단편화란 한 마디로 공간 낭비라 설명할 수 있습니다. 외부 단편화와 달리 메모리 공간에 프로세스 실행에 필요한 데이터가 적재될 공간이 충분히 있고 적재될 수 있지만 적재되고 나서 빈 영역이 발생하는 것입니다.

Q10. 세그멘테이션의 장단점은 무엇인가?

페이징 기법이 가지는 내부 단편화 문제를 극복하기 위해 세그멘테이션 기법이 사용됩니다. 페이지는 기본적으로 4KB 단위로 만들어집니다. 때문에 만약 9KB짜리 프로세스를 실행해야 한다면 메모리 공간에 12KB가 할당되고 3KB의 사용되지 못하고 낭비되는 영역이 만들어집니다. 세그멘테이션은 페이징과 똑같이 메모리 관리 기법이지만 차이점은 분할 방식입니다. 페이징은 한 단위를 기준으로 정적으로 분할하지만 세그멘테이션은 동적으로 분할하여 내부 단편화가 발생하지 않도록 합니다. 하지만 이런 세그멘테이션은 내부 단편화를 해결한다는 장점이 있지만 페이징에 비해 상대적으로 복잡한 메모리 관리로 오버헤드가 발생할 수 있다는 단점이 있습니다.

Q11. 임계 영역에 대해 설명하라.

임계 영역은 둘 이상의 쓰레드가 공유자원에 접근하는 데 있어 한 번에 한 쓰레드만 접근할 수 있도록 보장하는 영역을 말합니다. 임계 영역을 둠으로써 쓰레드는 공유자원에 대한 배타적인 사용권을 보장받을 수 있습니다. 이러한 임계 영역을 두기 위해 사용하는 방법으로 크게 뮤텍스와 세마포어가 있습니다.

Q12. 뮤텍스(Mutal Exclusion, Mutex)와 세마포어(Semaphore)의 차이를 설명하라.

뮤텍스 즉 상호배제란 임계 영역에 접근하는 쓰레드 간의 충돌을 막기 위해 사용하는 기법입니다. 이를 위해 Lock을 사용해서 임계영역에 들어가는 쓰레드가 Lock을 걸어 다른 쓰레드가 임계 영역으로 들어오지 못하도록 하고 이후 나갈 때 Lock을 해제하는 방식으로 다른 쓰레드가 임계 영역으로 들어올 수 있도록 하는 방법입니다. 세마포어 또한 임계 영역에 접근하는 쓰레드 간의 충돌을 막기 위해 사용하는 기법입니다. 기본적으로 뮤텍스와 동일하지만 차이점이 있다면 뮤텍스는 임계 영역에 들어간 쓰레드가 Lock을 걸고 해제할 수 있는 Locking 메커니즘을 사용하는 반면 세마포어는 Lock을 걸지 않은 쓰레드도 Lock을 해제할 수 있는 Signaling 메커니즘을 사용합니다.

Q13. 스케쥴링에 대해 설명하시오.

스케쥴링은 프로세스를 실행시키기 위해 CPU의 자원을 할당하는 정책을 계획하는 것입니다. 이 CPU 스케쥴링이 필요한 이유는 CPU 자원을 프로세스에게 효율적으로 할당하여 더 많은 작업을 처리할 수 있는 처리 속도를 높이기 위함입니다. 스케쥴링 방식에는 크게 선점형 스케쥴링과, 비선점형 스케쥴링이 있습니다. 선점형 스케쥴링은 한 프로세스가 CPU를 할당받아 실행되고 있을 때 우선순위가 다른 프로세스가 CPU를 강제로 점유할 수 있도록하는 기법입니다. 종류로는 라운드로빈, SRT ,다단계 큐, 다단계 피드백 큐 등의 알고리즘이 있습니다. 반면 비선점형 스케쥴링은 한 프로세스가 CPU를 항당받아 실행되고 있을 때 다른 우선 순위높은 프로세스가 CPU를 강제로 빼앗아 점유할 수 없는 기법입니다. 종류로는 FCFS, SJF, HRN 등의 알고리즘이 있습니다.

Q13-1. 스케쥴링 알고리즘에 대해 설명해주세요. (예상)

FCFS(First-Come First-Served)는 큐에 먼저 도착한 프로세스 순서대로 스케쥴링 하는 방식입니다. 비선점 스케쥴링에 방식에 해당합니다. 이런 FCFS의 단점은 CPU를 장기간 독점하는 프로세스가 있다면 다른 프로세스가 실행되지 못하고 오래 기다려야 한다는 단점이 있습니다. 이러한 단점을 보완하기 위해 SJF(Shortest-Job-First) 기법이 사용됩니다. CPU 작업시간이 짧은 프로세스 순서대로 스케쥴링하는 방식입니다. 비선점 스케쥴링 방식에 해당합니다. 특징은 만약 CPU 작업시간이 동일할 경우 FCFS 정책을 따릅니다. 이 SJF의 장점은 프로세스의 평균 대기 시간이 최소화된다는 것이며 단점은 CPU 작업시간에 대한 정확한 계산이 가능하지 않고, CPU 작업 시간이 긴 프로세스는 오랜시간 CPU를 할당받지 못할 수 있습니다. FCFS와 동일하게 이런 점유 불평등 현상이 있는 SFJ 알고리즘을 보완하기 위해 우선순위를 기반으로하는 HRN(Highest Response-ratio Next) 방식이 사용됩니다. 우선 순위는 $(대기시간 + 실행시간) \over (실행 시간)$로 계산 됩니다. 이외에도 여러 스케쥴링 알고리즘이 있지만 가장 일반적으로 사용하는 것은 Round Robin입니다. RR은 FCFS와 마찬가지로 순차적으로 스케쥴링을 진행하지만 특징은 동일한 시간의 Time Quantum만큼 CPU를 할당해 프로세스를 실행하는 방식입니다. RR 방식은 공정하다는 장점이 있지만 반면 Time Quantum이 커지면 FCFS와 같아진다는 단점이 있고, 작다면 Context Switcing이 많아져 오버헤드가 증가하는 단점이 있습니다.

Q14. Context Swiching에 대해 설명하라. (예상)

CPU가 어떤 프로세스를 실행 중일 때 인터럽트에 의해 다른 프로세스를 실행시켜야 하는 경우 기존 실행되던 프로세스 상태를 PCB에 저장하고 새로운 프로세스를 메모리에 적재하는 방법입니다. Context Swiching이 되면 실행될 프로세스의 PCB에 있는 정보와 레지스터 값을 읽어온 다음 이어서 작업을 수행합니다. 이 Context Swiching이 많이 일어나면 오버헤드가 발생하므로 Context Switching을 일으키는 스케쥴러가 최소한으로 Context Swiching이 일어나도록하는 스케쥴러 알고리즘을 사용해야 합니다.

Q15. Call By Value와 Call By Reference의 차이에 대해 설명하시오.

Call By Value란 Call By Reference는 함수에 인자를 전달하는 두 방식입니다. Call By Value는 전달받은 인자를 함수 내에서 복사해서 사용하는 것을 의미합니다. 복사해서 사용하기 때문에 원래 값에 영향을 미치지 않습니다. 반면 Call By Reference는 메모리 주소값에 있는 값을 직접 참조하는 방식입니다. 따라서 원래 값에 영향을 미치는 방식입니다. 

Q16. PNG와 JPG의 차이를 설명하라.

Q17. 다이나믹 프로그래밍이란 무엇인가? 또 신경망의 관점에서는 어떻게 활용되는가?

DP는 큰 문제를 작은 문제로 나누어 푸는 방법입니다. 분할정복 알고리즘과 같이 큰 문제를 작은 문제로 나누어 푼다는 점에서 공통점을 가집니다. 하지만 차이점은 작은 문제 계산에 있어 반복이 일어나지 않는다는 것입니다. 일반적으로 DP는 점화식을 세워 문제를 해결합니다. 또 memoization을 이용해 한 번 계산해둔 값을 다시 활용한다는 특징이 있습니다. 가장 쉬운 예시로는 피보나치 수열이 있습니다. 즉 다음 수열의 값은 현재 수열 값과 이전 수열 값의 합입니다. 1, 1, 2, 3, 5, 8로 증가하는 형태를 가지며 다음 수열을 구할 때 이미 구해두었던 수열의 값을 활용합니다.

신경망의 관점에서 역전파를 진행할 때 다이나믹 프로그래밍을 사용합니다. back-propagation하면서 gradient를 전부 계산하는 것이 아니라 마지막 출력노드에서 한 번 미분값을 계산한 뒤 backward 방향의 노드로 전달하면서 재사용합니다.

Q18. 백트래킹 알고리즘에 대해 설명하라.

백트래킹 알고리즘이란 해를 찾는 도중 해가 아니라고 판단될 경우 되돌아가서 다시 해를 찾는 방법입니다. 백트래킹 알고리즘은 일반적으로 DFS와 함께 사용됩니다. DFS는 알고리즘은 가능한 모든 경로를 탐색하기 때문에 계산 비용이 많이 발생합니다. 이를 해결하기 위해 가지치기가 필요한데 이 때 사용하는 것이 백트래킹 알고리즘입니다. 대표적인 예제로 N-Queen 문제가 있습니다. 

Q19. 거의 정렬이 이뤄졌을 때 사용하면 좋은 정렬 알고리즘은 어떤 것인가?

삽입 정렬을 사용하면 좋습니다. 삽입 정렬은 정렬할 원소보다 index가 낮은 곳에 있는 원소들을 탐색해 정렬하는 알고리즘 입니다. 동작은 두 번째 index에 있는 원소부터 시작합니다. 삽입 정렬의 특징은 알고리즘이 동작하는 동안 반드시 맨 왼쪽 index까지 탐색하지 않아도 됩니다. 앞 부분은 이미 정렬 되어 있기 때문에 정렬 하고자 하는 원소보다 작아지는 경우 다음에만 삽입하면 됩니다. 거의 정렬이 모두 이뤄져있다면 모든 원소가 한 번씩만 비교하므로 $O(n)$의 복잡도를 가집니다.

Q20. 대칭키 암호화와 비대칭키 암호화는 무엇인가?

대칭키 암호화는 암복호화에 사용하는 키가 동일한 방식의 암호화입니다. 종류로는DES, 3DES, AES, SEED, ARIA 등이 있습니다. 장점으로는 비대칭키 암/복호화에 비해 수행 시간이 짧습니다. 반면 키교환문제가 발생한다는 단점이 있습니다. 비대칭키 암호화는 암복호화에 사용하는 키를 서로 달리하는 방식의 암호화입니다. 종류로는 RSA, ElGamal, ECC 등이 있습니다. 장점은 공개키가 있고 개인키가 있기 있기 때문에 키 교환 문제가 발생하지 않습니다. 단점은 대칭키에 비해 암복호화 수행시간이 느리다는 것이 있습니다.

Q20-1. 비대칭키는 왜 공개키와 비밀키로 나뉘는가?

키교환 문제를 해결하기 위해 사용합니다. 대칭키는 암호화와 복호화에 사용하는 키가 같기 때문에 이 키를 전달하는 과정에서 탈취될 가능성이 존재합니다. 반면 비대칭키는 공개키가 공개되어 있기 때문에 키교환 문제가 발생하지 않습니다. 동작방식은 가령 A와 B가 있을 때 B가 공개키/개인키 쌍을 생성합니다. A는 전달하고자 하는 정보를 B의 공개키로 암호화해서 B에게 주면 B는 자신의 개인키를 이용해 복호화를 수행하는 방식으로 이루어집니다.

Q21. TCP/UDP 차이를 설명하라.

TCP는 연결지향형 프로토콜이고 UDP는 비연결지향형 프로토콜입니다. 연결지향형이랑 클라이언트와 서버가 연결된 상태에서 데이터를 주고 받습니다. 반면 비연결지향형은 클라이언트와 서버가 연결되지 않은채로 데이터를 일방적으로 전송합니다. TCP를 사용하기 위해서는 3-way handshaking 과정을 거쳐야 합니다. 클라이언트는 SYN 플래그를 보내면 서버는 SYN + ACK를 보내고 다시 클라이언트는 ACK를 보냄으로써 상호 연결됩니다. 이러한 TCP의 특징은 데이터의 전송순서를 보장하고 수신여부를 확인합니다. 때문에 신뢰성이 높다는 장점이 있습니다. 반면 UDP보다 데이터 전송속도가 느리다는 단점이 있습니다. UDP는 3-way handshaking 과정 없이 데이터를 일방적으로 전송합니다. UDP의 특징은 데이터의 전송 순서가 보장되지 않으며 수신 여부를 확인하지 않습니다. 따라서 신뢰성이 낮다는 단점이 있습니다. 반면 TCP에 비해 속도가 빠르다는 장점이 있습니다.

Q22. 공유기 동작은 어떻게 이루어지는가?

공유기에 LAN 선을 연결하게 되면 공인 IP가 부여됩니다. 이 공유기에 장치를 연결하면 NAT에 의해 공인 IP가 사설 IP로 변경되어 할당됩니다. 공인 IP는 외부 인터넷과 연결을 위해 사용하고 사설 IP는 내부 인터넷 사용을 위해 사용합니다. 내부 인터넷에서 외부 인터넷으로 연결하기 위해서는 NAT를 통해 다시 공인 IP로 변경됩니다. 이 때 연결 요청이나 자원 요청에 대한 응답을 받기 위해서는 PAT를 통해 사설 IP에 할당된 포트정보까지 매핑시킴으로써 특정 디바이스를 식별할 수 있습니다. 만약 내부의 요청 없이 곧 바로 외부에서 내부로 접근하기 위해서는 포트포워딩을 통해 접속할 수 있습니다. 

Q23. RESTful에 대해 설명하라. 또 단점은 무엇인가? 

REST는 HTTP 프로토콜을 통해 DB에 Create, Read, Update, Delete 연산을 수행하는 것을 의미합니다. client-server 구조를 갖는게 REST의 특징 중 하나입니다. 하지만 클라이언트가 직접 DB에 접근하는 것을 위험하므로 REST API를 두어 서버가 데이터베이스에 클라이언트의 요청을 수행하고 결과를 반환합니다. 이러한 요청을 위해 HTTP METHOD를 사용하며 종류로는 GET, POST, PUT, DELETE 등이 있습니다. RESTful은 이러한 REST 아키텍처의 특징을 잘 지켜 설계한 것을 의미합니다. "REST API를 제공하는 웹 서비스는 RESTful하다"와 같이 표현할 때 사용됩니다. 이러한 REST 또는 RESTful의 장점은 쉽게 사용할 수 있다는 것입니다. REST API 메시지를 읽는 것만으로 의도하는 바를 명확히 파악할 수 있습니다. 반면 표준이 존재하지 않는다는 단점이 있습니다.

Q24. NoSQL의 장단점을 이야기하라.

NoSQL은 일반적으로 RDBMS와 함께 언급됩니다. 먼저 NoSQL의 장점은 정해진 스키마가 없기 때문에 데이터 구조가 유연하고 자유롭게 컬럼을 추가할 수 있습니다. 또 대용량 처리에 적합합니다. 반면 단점으로는 정해진 스키마가 없기 때문에 데이터의 일관성이 없습니다. 또 중복이 발생할 수 있고 발생할 경우 계속해서 모든 컬렉션에서 업데이트해야하는 번거로움이 있습니다. RDMBS의 장점은 정해진 스키마가 있기 때문에 데이터 구조의 일관성이 보장됩니다. 또 데이터의 중복이 발생하지 않습니다. 반면 단점으로는 정해진 스키마가 있기에 유연성이 떨어집니다. 또 규모가 커질수록 테이블 간 JOIN이 복잡해지고 쿼리 프로세싱도 복잡해져 성능이 저하됩니다. 

Reference

[1] [운영체제] 페이징과 세그멘테이션 (제이온)

[2] [OS] 세마포어(Semaphore) vs 뮤텍스(Mutex) 차이 (망나니개발자, MangKyu)

[3] [운영체제] CPU 스케줄링이란? (그적)

[4] [운영체제] CPU 스케줄링 (제이온)

[5] [운영체제OS]8. 가상메모리(페이징, 페이지 교체, 스레싱)

[6] 알고리즘 - Dynamic Programming(동적프로그래밍)이란? (전준엽)

[7] [암호학] 대칭키 vs 공개키(비대칭키) 암호화 차이 (leeforest)

[8] [Network] TCP / UDP의 개념과 특징, 차이점 (코딩팩토리)

[9] 랜덤 포레스트(Random Forest) 쉽게 이해하기 (아무튼 워라밸)

[10] [ML] XGBoost 개념 이해 (최우노)

[11] 벨만 방정식 (subsay)

[12] Training, Validation and Test sets 차이 및 정확한 용도 (훈련, 검정, 테스트 데이터 차이) (네이쳐k)

[13] 딥러닝 모델의 K-겹 교차검증 (K-fold Cross Validation) (DEEPPLAY)

[14] Hidden Markov Model (은닉 마르코프 모델) (Bioinformatics And Me)

[15] 인공지능의 이해 (5/6): 순환 신경망 (RNN) (라인하트)

[16] [딥러닝][NLP] LSTM(Long Short Term Memory Networks) (Hyen4110)

[17] Long Short-Term Memory (LSTM) 이해하기 (개발새발로그)

[18] CNN (Convolutional Neural Network) 개념 (강성욱)

[19] 배치 정규화(Batch Normalization)

1. 회귀분석이란?

회귀분석은 가장 단순화하면 독립변수(x)로 종속변수(y)를 예측하는 것을 의미한다. 이를 풀어 쓰자면 회귀분석이란 독립변수가 종속변수에 미치는 영향력을 측정하고 이를 기반으로 독립변수의 특정값에 대응하는 종속변수값을 예측하는 모델을 만드는 통계적 방법론이다. 회귀분석의 목적은 독립변수로 종속변수를 설명하는데 있다. 회귀분석에서는 독립변수와 종속변수를 동일하지만 다양한 이름으로 부른다. 독립변수의 경우 설명변수, 예측변수, 원인변수 등으로 불리고 종속변수의 경우 목표변수, 목적변수, 반응변수, 결과변수 등으로 불린다. 이를 혼동하지 않기 위해서는 이름들이 원인측에 가까운지 결과측에 가까운지 또 종속성의 여부를 떠올려 추론하면 될 것이다. 이러한 회귀분석을 진행하기 위한 전제조건은 4~5가지 기본 가정이 어긋나지 않아야 한다.

1.1 회귀분석의 기본 가정

회귀분석을 진행하기 위해 갖춰져야할 기본 몇 가지 가정이 있다. 일반적으로 4대 가정 또는 5대 가정이라 불리며 4대 가정은 앞글자를 따서 LINE이라 불린다.

• 선형성(Linearity): 모든 독립변수와 종속변수 사이에는 선형적인 관계를 띠어야 한다.
• 독립성(Independence): 1) 잔차 사이에는 상관관계 없이 독립적이어야 한다. 2) 잔차와 독립변수 간 상관관계가 없어야 한다.
• 정규성(Normality): 잔차가 평균이 0인 정규분포를 띠어야 한다. $E(\epsilon_i|X_i) = 0$
• 등분산성(Equal Variance): 잔차의 분산은 독립변수와 무관하게 일정해야 한다.
• 다중공선성(No Multicollinearity): 독립변수 간의 강한 상관관계가 있을 때의 성질을 의미하는 것으로 이러한 성질이 없어야 회귀분석이 가능하다.

여기서 중요한 것은 독립변수의 정규성, 독립성, 등분산성, 선형성을 고려하는 것이 아니라 잔차의 정규성, 독립성, 등분산성, 선형성을 따져야 한다. 여기서 잔차란 표본집단의 관측값에서 예측값을 뺀 값이다. 유사하게 사용되는 오차는 모집단에서 관측값에서 예측값을 뺀 값을 뜻한다.

또 만약 잔차의 등분산성이 성립하지 않을 경우 가중최소제곱법(Weighted Least Sqaure)을 사용해 잔차의 이분산성을 해결할 수 있다. 이분산성이란 데이터에 일반적인 최소제곱법을 적용할 경우 추정통계량의 신뢰도가 상실되어 회귀계수의 표준오차를 과소추정 또는 과대추정하게 되는 성질을 말한다. 이러한 이분산성은 가중최소제곱을 사용하면 회귀 모수의 오차항 분산에 반비례하는 가중치를 부여하여 가중 오차제곱합을 최소화하는 방법이다. (출처: Tony Park)

1.2 회귀분석의 종류와 특징

회귀분석은 크게 두 가지로 선형회귀분석과 로지스틱회귀분석으로 나뉜다. 선형회귀분석은 연속형 종속변수를 사용하며 분석 목적은 예측에 있다. 또 선형회귀분석은 모델을 찾기 위해 최소자승법을 사용하고 모델을 검정하기 위해 t검정, F검정 등을 사용한다. 선형회귀분석은 다시 단순 선형회귀분석과 다중 선형회귀분석, 비선형 회귀분석 셋으로 나뉜다. 단순 선형회귀분석은 독립변수가 1개 종속변수가 1개일 때 진행하는 분석이다. 다중 선형회귀분석은 독립변수가 여러 개고 종속변수가 1개일 때 진행하는 분석이다. 비선형회귀분석은 단순/다중 선형회귀분석처럼 선형으로 나타나는 식이 아니라 2차함수나 지수함수와 같이 비선형으로 나타내는 관계에 대해 분석하는 방법이다.

로지스틱회귀분석은 독립변수와 범주형 종속변수 간의 관계를 모형화하여 종속변수를 분석하거나 분류하는 통계적인 방법론이다. 로지스틱회귀분석은 범주형 연속변수를 사용하며 분석 목적은 분류에 있다. 로지스틱회귀분석은 모델을 찾기 위해 최대 우도법을 사용하고 모델 검정을 위해 카이제곱 검정 등을 사용한다.

1.3 회귀분석의 절차는?

1. 가설 수립: 귀무 가설과 대립 가설 설정
2. 데이터 경향성 확인: 독립변수와 종속변수 간 산점도 분석과 상관관계 분석 진행
3. 모델 적합성 확인: 결정계수, 분산분석, 잔차기본 가정(정규성, 등분산성, 독립성 등) 확인
4. 회귀계수 계산 및 유의성 확인: 독립변수 간 다중공선성, t검정을 통한 회귀계수 유의성, 독립변수 선택 및 해석
5. 모델 선정: 모델 적합성과 오차의 기본 가정 확인을 통해 모델 선정

1.4 결정계수란?

결정계수란 통계학에서 수행하는 회귀분석의 회귀식의 정확도를 평가하기 위한 척도(measure)이다. 다르게 말하면 독립변수를 통해 종속변수를 예측한 것의 설득력을 나타내는 척도라 할 수 있다. 이 결정계수를 사용하는 이유는 회귀분석에서 예측을 하더라도 실제값과의 오차가 발생할 수 밖에 없기 때문이다.

이 오차라는 것은 점의 밀도에 따라 달라진다. 예를 들어 많은 점이 모여 있어 밀도가 촘촘한 경우 예측값과 실제값의 오차가 작아진다. 반면 점들이 밀도가 느슨할 경우 예측값과 실제값의 오차가 커진다. 즉 점의 밀도, 데이터 수에 따라 오차의 크기가 달라지고 이에 따른 회귀식의 정확도가 달라지는 것이다.

위와 같이 밀도에 따라 회귀식의 오차가 달라지고 정확도가 달라지므로 이 정확도를 평가하기 위한 척도가 결정계수이다. 이 결정계수는 R-square라 부르며 $R^2$로 나타낸다. 여기서 R은 비율(Rate)를 나타낸다. 이 결정계수는 두 가지 방법으로 나뉘어 사용된다.

첫 번째는 피어슨 상관계수를 이용하는 방법이다. 결과적으로 결정계수는 피어슨 상관계수를 제곱한 값이라 할 수 있다. 피어슨 상관계수의 범위는 $-1 \leq R \leq 1$을 가지는데, 제곱하면 값의 범위가 $0 \leq R^2 \leq 1$된다. 하지만 이렇게 제곱할 수 있을 때는 후에 설명할 단순회귀분석처럼 독립변수가 하나인 경우로 제한된다. 예를 들어 $y=ax+ b$일 경우 결정계수는 독립변수 x와 종속변수 y의 상관계수의 제곱이다. 하지만 다중회귀분석처럼 $y = ax_1x_1 + b_1 + a_2x_2 + b_2$처럼 독립변수가 $x_1, x_2$로 2개 이상일 경우 $x_1, y$와 $x_2, y$의 두 상관계수를 각각 구해야 한다. 다시 돌아와 피어슨 상관계수를 제곱한 결정계수는 아래와 같은 수식으로 나타낸다.

$\displaystyle R^2 = {\sum (y_i - \hat{y}) \over \sum (y_i - \hat{y})^2}$

수식이 의미하는 바는 전체 변동 대비 회귀선에 의해 설명되는 변동이 얼마나 되는지를 보는 것이다.

만약 섭취열량(독립변수)이 얼마나 비만(종속변수)에 영향력을 미치는가를 알고 싶다고 가정하고 결정계수가 $R^2 = 0.8$이 계산되었을 경우, 섭취열량이라는 독립변수를 통해 80%정도 비만이라는 종속변수를 설명(설득)할 수 있다고 해석할 수 있다.

두 번째는 분산분석의 데이터를 활용하는 것이다. 분산분석에서는 SST, SSR, SSE의 개념이 사용된다. SST는 총제곱합, SSR는 회귀제곱합, SSE는 잔차제곱합을 뜻하며 각각은 수식으로 다음과 같이 나타낸다.

$SSR = \sum(\hat{y_i}-\bar{y})^2$
$SSE = \sum(y_i - \hat{y}_i)^2$
$SST = SSR + SSE = \sum_{i=1}^n(y_i-\bar{y})^2$

결과적으로 SSR이 얼마나 크고 SSE가 얼마나 작냐에 따라 회귀식에서 산출된 정확도가 결정된다. 즉 결론적으로 결정계수 $R^2$이 0에 가까울수록 회귀식의 정확도는 낮고, 1에 가까울수록 회귀식의 정확도는 높다고 할 수 있다.

이러한 결정계수는 독립변수가 많아질수록 값이 커진다는 특성을 갖는다. 따라서 종속변수를 잘 설명하지 못하는 독립변수가 추가되더라도 결정계수값이 커질 수 있다. 이러한 한계점을 보완하고자 수정된 결정계수(adjusted coefficient of determination)을 사용한다. 이 수정된 결정계수는 표본 개수와 독립변수 개수를 고려해 계산하며 식은 다음과 같다.

adjusted $R^2 = {1 - {n-1 \over (n-p-1)(1-R^2)}}$

만약 단순회귀분석을 진행한다면 결정계수를 사용하면 되고, 다중회귀분석을 진행한다면 수정된 결정계수를 사용하는 것이 좋다. 이러한 결정계수와 수정된 결정계수를 계산하더라도 정확도를 판단하기 모호한 경우가 생긴다 극단적으로 0과 1이라면 정확도를 판별할 수 있지만 0.4나 0.6과 같이 값이 모호하다면 올바른 의사결정이 어려워진다. 따라서 추가적으로 가설검정을 통해 이러한 의사결정이 이루어진다.

1.5 회귀계수 계산

회귀 모델이 선택된다면 이에 대한 회귀계수를 계산하고 유의성을 검정해야 한다. 회귀계수를 구하기 위해서 회귀선의 기울기와 절편을 구해야하며 이는 최소제곱법(Least Square Method)로 계산할 수 있다. 최소제곱법은 잔차의 제곱 합(Sum of Squared Error, SSE)이 최소가 되는 회귀선을 찾는 방법이다. 잔차의 제곱 합 SSE는 다음과 같은 수식으로 나타낸다.

$\displaystyle SSE = \sum_{i=1}^n \epsilon_i^2 = \sum_{i=1}^n (y_i-\hat{y}_i)^2 = \sum_{i=1}^n (y_i - \beta_0 - \beta_1x_i)^2$

위 식에서 $\beta_0$은 절편 $\beta_1$은 기울기를 나타낸다. 각각을 편미분함으로써 절편과 기울기의 추정값을 구할 수 있고 그 결과는 아래와 같다.

$\displaystyle \hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}$

$\displaystyle \hat{\beta}_1 = {\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \over \sum_{i=1}^n (x_i - \bar{x})^2}$

1.6 회귀분석 정규화 (Regularization)

11.01(화) 내 작성 예정
(다중공선성 해결을 위해 사용)

2. 상관관계 분석이란?

상관분석이란 두 변수간 상관성 정도를 알기 위해 사용하는 분석이다. 즉 상관분석의 목적은 임의의 두 변수 간의 상관성 정도를 보는 것이다. 상관분석을 통해 상관계수라는 수치로 정량화되어 표현된다. 이 상관계수는 대표적으로 3가지를 사용한다. 피어슨 상관계수, 스피어만 상관계수, 켄달 상관계수이다. 이 상관계수들은 아래의 데이터 종류에 따라 달리 사용된다.

2.1 상관계수의 종류

피어슨 상관계수 (모수적)
피어슨 상관계수란 키/몸무게 같이 분석코자 하는 두 변수가 모두 연속형 데이터일 때 사용하는 척도다. 피어슨 상관계수 사용을 위해 두 변수 모두 정규성을 따른다는 가정이 필요하다. 때문에 피어슨 상관계수는 두 변수간 선형적인 관계를 모수적 방법으로 나타내는 척도라고 할 수 있다. 또 피어슨 상관계수는 독립변수와 종속변수 간의 선형관계를 나타내는 척도이다. 피어슨 상관계수의 동일한 의미의 다른 이름은 피어슨 적률 상관계수, 피어슨 r, R 등이 있다. 또 일반적으로 상관계수라 하는 것은 피어슨 상관계수를 뜻한다. 피어슨 상관계수는 $-1 \leq R \leq 1$ 범위의 값을 갖는다. 0에 가까울수록 두 변수간 선형적 관계가 없고, -1에 가까울수록 음의 상관관계를 가지며 +1에 가까울수록 양의 상관관계를 가진다. 피어슨 상관계수의 수식은 다음과 같이 정의된다.

$\displaystyle R = {cov(x, y) \over \sqrt{var(x)var(y)}} = {\sum_i^n (x_i - \bar{x})(y_i - \bar{y}) \over \sqrt{\sum_i^n (x_i-\bar{x})^2(y_i-\bar{y})^2}}$

$n$: 표본집단 수
$\bar{x}$: 표본집단 $X$의 평균
$\bar{y}$: 표본집단 $Y$의 평균

위 수식을 통해 표본 집단으로부터 표본 상관계수를 계산할 수 있다. 표본 상관계수가 도출되면 다음으로 이 상관계수의 타당성을 위해 가설검증을 진행한뒤 가설검증 결과를 기반으로 가장 처음 수립했던 가설의 채택을 결정한다.

스피어만 상관계수 (비모수적)
분석하고자 하는 두 변수가 회귀분석의 기본 가정 중 하나인 정규성을 충족하지 않을 경우 피어슨 상관계수를 사용할 수 없다는 한계점을 극복하기 위해 사용한다. 스피어만 상관계수는 스피어만 순위 상관계수, 스피어만 $r_s$ 라고도 불린다. 순위를 이용하기에 비모수적인 방법에 해당하며 연속형 변수뿐만 아니라 순위형 변수에도 적용가능하단 특징이 있다. 예를 들어 수학 점수와 과학 점수와의 상관계수는 피어슨 상관계수로 구하고, 수학 과목 석차와 영어 과목 석차는 스피어만 상관계수로 계산할 수 있다. 스피어만 상관계수는 다음과 같은 수식으로 표현된다. 아래 수식에서 $d$는 관측값들의 등위 간 차이를 나타내고 $n$은 관측 데이터 수를 의미한다.

$\displaystyle r_s = 1 - {\sigma \sum d_i^2 \over n(n^2-1)}$

켄달 상관계수 (비모수적)
켄달 상관계수는 두 연속형 변수 간의 순위를 비교해 연관성을 계산하는 방법으로 순위 상관계수의 한 종류이다. 켄달 상관계수는 켄달타우 상관계수라고도 불린다. 켄달 상관계수는 피어슨 상관계수의 변수값이 정규분포를 따르지 않을 때 사용하기 어렵다는 단점을 보완하기 위해 사용한다. 켄달 상관계수를 계산하기 위한 핵심 개념은 concordant pair이다. 이는 각 변수의 비교 대상이 상하관계가 같을 때를 의미한다. 예를 들어 사람 a와 b의 키/몸무게를 비교했더니 사람 a가 모두 키/몸무게가 사람 b보다 크다면 concordant pair라고 말한다. 반면 사람 b와 c를 비교했을 때 b가 키는 크지만 몸무게는 c보다 작은 경우는 concordant pair가 아니다. 결과적으로 켄달 상관계수를 구하기 위한 수식은 다음과 같이 C와 D로 표현하며 여기서 C는 concordant pair한 수이며 D는 concordant pair하지 않은 수를 의미한다.

$\displaystyle {{C - D} \over {C + D}}$

간단 용어 정리

독립변수: 다른 변수에 영향을 받지 않는 변수이자 종속 변수에 영향을 주는 변수. 주로 입력이나 원인을 나타낸다.
종속변수: 독립 변수에 의해 영향을 받는 변수. 주로 출력이나 결과를 나타낸다.
표준오차: 표본평균들의 편차를 뜻한다.
회귀계수: 회귀분석에서 독립변수가 한 단위 변화함에 따라 종속변수에 미치는 영향력 크기다. 만약 두 변수간 상관관계가 없을 경우 회귀계수는 의미가 없게 된다.

Reference

[1] 설명 변수와 목적 변수 (두더지 개발자)
[2] 종속변수 vs 독립변수 (CodeDragon)
[3] 상관계수 & 결정계수 & 수정된 결정계수 (황금모찌)
[4] 결정계수란? (나부랭이의 수학블로그)
[5] 회귀분석에서의 분산분석과 결정계수/ Anova in Regression Analysis
[6] 상관분석_종류
[7] [통계] 회귀분석(Linear Regression) 정의, 특징, 종류 (Tony Park)
[8] [TIL] 회귀분석의 가정 (다람이도토리)
[9] 회귀 분석의 표준 가정 (Hooni's Playground)
[10] 상관계수와 결정계수의 관계
[11] 켄달타우 (Kendalltau) (Jukyoung LEE)

모수에 대한 포스팅은 아래 링크에서 참조 가능합니다.

[확률/통계] 모수 추정과 추정량, 추정치

모수적 방법과 비모수적 방법

통계학의 분석 방법은 모수(parameter)의 필요성 여부에 따라 모수적 방법과 비모수적 방법으로 분류된다. 모수란 입력 데이터의 분포를 가정(ex: 정규분포)하는 것을 의미하며, 비모수란 입력 데이터 분포를 가정하지 않음을 의미한다. 대부분의 분석법은 모수적 분석 방법에 해당한다. 하지만 만약 모수적 방법에서 가정했던 분포가 적합하지 않을 경우 입력 데이터의 특성을 잘 파악하지 못한 것이므로 비모수적 방법을 사용한다. 비모수적 방법은 입력 데이터에 대한 분포를 가정할 수 없는 경우에 사용하는 방법이다. 모수 방법에서 가정했던 입력 데이터 분포를 완화시키는 방식으로 사용한다.

머신러닝에서도 모수와 비모수가 적용되어 parametric model과 non parametric model 형태로 나타난다.

parametric model

파라미터 수가 결정된 모델을 의미한다. 파라미터 수가 결정된 이유는 입력 데이터가 어떤 분포를 따른다고 가정했기 때문이다. 따라서 non-parametric 모델과 달리 아무리 입력 데이터 양이 많더라도 학습해야 할 파라미터 수는 변하지 않는다. 이러한 parametric model의 종류는 Linear Regression, Logsitic Regression, CNN, RNN 등이 있다. 모델이 학습해야 할 parameter가 결정되어있기 때문에 non-parametric 방식에 비해 학습 속도가 빠르고 모델의 복잡성이 낮다는 장점이 있다. 반면 단점은 입력 데이터가 어떤 분포를 따른다는 가정이 있으므로 유연성이 낮고, non-parametric model에 비해 복잡한 문제를 해결하기 어렵다.

non-parametric model

파라미터 수가 결정되지 않은 모델을 의미한다. 입력 데이터가 어떤 분포를 따른다고 가정하지 않았기 때문이다. 따라서 non-parametric model은 입력 데이터에 대한 사전 지식이 없을 때 사용할 수 있다. 이러한 non-parametric model의 종류는 GAN이나 decision tree, random forest, k-nearest neighbor 등이 있다. 이런 non-parametric model은 어떤 분포를 다른다고 가정하지 않았기 때문에 parametric model에 비해 훨씬 유연성이 있다는 장점이 있다. 반면 parametric model에 비해 학습 속도가 느리거나, 더 많은 양의 데이터를 필요로 한다는 단점이 있다.

Reference

[1] Parametric model과 Non-parametric model (유니의 공부)

적률의 배경

적률추정법은 통계학의 근본이 되는 수리통계학에서 나오는 개념이다. 적률추정법을 이해하는데 있어 난관은 적률의 의미이다. 적률(moment)을 한마디로 나타내면 확률변수 $X$의 $n$제곱 기대값인 $E[X^n]$이다. 하지만 왜 이렇게 표현하는지를 이해하기 위해서는 적률의 의미를 살펴볼 필요가 있다. 모멘트(=적률)란 물리학에서 사용되는 개념으로 "어떤 물리량과 어떤 기준점 사이의 거리를 곱한 형태를 가지는 것 즉, 모멘트 = 물리량 * 거리"이다. 하지만 통계학에서 적률로의 직관적인 이해로 연결되지 않는다.

모멘트는 한 마디로 질량이 분포된 모양에 따라 그 효과가 달라지는 현상을 말한다. 예를 들어 몸무게 같은 두 명의 사람이 시소를 탄다고 하자. 이 때 두 사람이 모두 양 끝에 탔을 때랑, 한 사람은 끝에 한 사람은 한 칸 앞에 탔을 때 작용하는 모멘트가 달라지는 것과 같다. 즉 두 사람의 질량은 같아도 질량이 분포된 모양(거리)에 따라 효과가 달라지는 것이다.

다시 돌아와 앞전의 어떤 물리량이란 것은 질량, 힘, 길이 등이 될 수 있고 쉽게 (질량 x 거리), (힘 x 거리), (길이 x 거리)로 표현하는 것을 모멘트(=적률)이라고 한다. 참고로 모멘트와 모멘텀(Momentum)이 비슷해 혼동되기도 하는데 이 둘은 다른 개념이다. 모멘텀은 운동량을 의미하는 것으로 모멘텀(운동량) = 질량(Mass) * 속도(Velocity)이다. 예를 들어 거대한 선박이 있다면 질량이 크고 속도는 작은 운동량을 가질 것이고, 어떤 총알이 날아간다면 질량은 작고 속도는 큰 운동량을 가진다.

통계학에서의 적률의 의미와 정의

그렇다면 이 적률(모멘트)은 왜 통계에서 사용할까? 그 이유는 위 언급한 "분포"와 관련있기 때문이다. 물리학에서 모멘트는 앞서 시소 예제와 같이 질량과 거리에 따라 달라졌다. 통계학에서의 적률은 확률과 확률변수에 따라 적률이 달라진다. 질량이 확률로, 거리가 확률변수로 바뀐 것이다. 그렇다면 이제 통계에서의 적률의 의미를 살펴보자. 적률은 초반부에 설명했듯 한 마디로 확률변수 $X$의 $n$제곱의 기대값인 $\mu_n = E[X^n]$으로 표현한다. 이 때의 양수 $n$은 차수를 뜻하는 것으로 확률변수 $X$의 $n$차 적률이라 한다. 이러한 적률이 중요한 이유는 확률분포의 특징을 설명하는 지표로서 역할을 하기 때문이다. 예를 들어 1차 적률은 확률변수의 평균을 나타내고, 2차 중심적률은 분산, 3차 중심적률은 왜도(skewness), 4차 중심적률은 첨도(kurtosis)를 나타낸다. 여기서 왜도란 확률밀도함수의 비대칭성을 나타내는 척도이며, 첨도는 확률밀도함수의 뾰족한 정도를 뜻하는 척도다. 

즉 확률분포의 특징을 나타내는 척도(Measure)는 4가지로 평균, 분산, 왜도, 첨도가 있고 이는 적률의 확률분포 X의 n제곱의 기대값을 통해 나타낼 수 있다. 평균은 원점에 대한 1차 모멘트로 $E[X]$로 표현하고 분산은 평균에 대한 2차 모멘트로 $E[(X-\mu)^2]$로 표현한다. 또 왜도는 평균에 대한 3차 모멘트로 $E[(X-\mu)^3]$로 표현하고 첨도는 평균에 대한 4차 모멘트로 $E[(X-\mu)^4]$로 표현한다. 만약 여기에 상수 $c$가 있다면 확률변수 $X$의 $n$차 적률은 $E[(X-c)^n]$로 표현한다. 이 때 $c=0$이면 원적률(적률)이라 하고 $c=E[X]$라면 중심적률이라 한다. 만약 어떤 두 확률변수의 모든 적률이 일치한다면 두 확률변수는 같은 분포를 가진다고 말할 수 있다. 이 특징이 가장 중요하다. 후에 모수 추정을 위해 사용하는 적률추정법의 원리가 되기 때문이다.

원점에 대한 $n$차 적률을 수식으로 나타내면 크게 이산확률변수와 연속확률변수로 표현할 수 있고 아래와 같다.

$\displaystyle E[X^n] = \begin{cases} \mbox{이산확률변수:} \sum_x x^n f(x)  \\ \mbox{연속확률변수:} \int_{-\infty}^{\infty} x^n f(x)dx \end{cases}$

이 때 $f(x)$는 이산확률변수에선 확률질량함수가 되고 연속확률변수에선 확률밀도함수가 된다. 위 정의에 따라 $n=1$을 대입하면 일반적으로 알고 있던 확률변수 X의 기대값이 된다. 즉 원점에 대한 1차 적률이 지금껏 알고 있던 기대값이다. 

적률생성함수의 필요성과 정의

적률의 수식 정의에 따라 연속확률변수에서 적률을 구하기 위해 적분을 해야하지만 적분 계산이 어렵거나 불가능한 경우도 있기 때문에 이러한 상황을 해결하고자 적률생성함수(Moment Generating Function, MGF)를 만들어 사용한다. 적률생성함수는 적률과 마찬가지로 이산확률변수와 연속확률변수로 나뉘어 다음과 같이 정의된다.

$\displaystyle M_X(t) = E[e^{tX}] = \begin{cases} \mbox{이산확률변수:} \sum_x e^{tx}f(x) \\ \mbox{연속확률변수:} \int_{-\infty}^\infty e^{tx}f(x)dx \end{cases}$

이 적률생성함수에서 n차 적률을 구하기 위해서는 적률생성함수를 $t$를 $n$번 미분하면 된다. 이 때 테일러 급수를 사용한다. 테일러 급수는 어떤 함수 $f(x)$를 다항함수 형태로 바꿔주는 방법이다. 테일러 급수는 아래와 같이 전개할 수 있다.

$\displaystyle f(x) = f(a) + f'(a)(x-a) + {1\over 2!}f''(a)(x-a)^2 + {1\over 3!}f'''(a)(x-a)^3 + \dots$

이를 적률생성함수의 기대값 속의 $e^{tX}$에 적용하면 다음과 같이 테일러 전개가 가능하다. ($f(t) = e^{tX}$)

$\displaystyle f(t) = e^{tX} = e^{aX} + Xe^{aX}(t-a)+ {1\over 2!}X^2e^{aX}(t-a)^2+ {1\over 3!}X^3e^{aX}(t-a)^3+ \dots$

다음으로 $a=0$을 대입하여 매클로린 급수 형태로 만들어준다. 테일러 급수는 일반적으로 무한한 항을 모두 사용하는 것이 아니라 저차원의 일부 항만 사용하여 근사하는 형태로 활용한다. 고차원 항을 많이 사용하면 어떤 함수 $f(x)$에 매우 가까워지지만 그만큼 계산 비용이 많이 발생하게 되기 때문이다. 그래서 $a=0$을 대입하는 이유는 테일러 급수에 직접 대입해본다면 하나의 항을 제외한 모든 항이 사라져 $f(x) = f(a)$만 남게 되어 구하고자 하는 값을 곧바로 얻을 수 있기 때문이다. 적률생성함수에선 $t=0$일 때의 값을 사용하므로 $a=0$을 대입하면 다음과 같아진다.

$\displaystyle e^{tX} = 1 + Xt + {1\over 2!}X^2t^2+ {1\over 3!}X^3t^3 + \dots$  

이를 원래 적률생성함수에 대입하게 되면 다음과 같아진다.

$\displaystyle M_X(t) = E[e^{tX}] = E[1+Xt+{1\over 2!}X^2t^2 + {1\over 3!}X^3t^3 \dots]$

위의 기대값 내부에 있는 항을 분리해서 표현하면 다음과 같아진다.

$\displaystyle = 1 + E[Xt] + E[{1\over 2!}X^2t^2] + E[{1\over 3!}X^3t^3] + \dots$

기대값과 무관한 항을 앞으로 빼주면 다음과 같다.

$\displaystyle = 1 + E[X]t + {1\over 2!}E[X^2]t^2 + {1\over 3!}E[X^3]t^3+ \dots$

따라서 적률생성함수는 다음과 같다.

$\displaystyle M_X(t) =  1 + E[x]t + {1\over 2!}E[X^2]t^2 + {1\over 3!}E[X^3]t^3+ \dots$

여기서 구한 적률생성함수는 미분을 통해 사용한다. 만약 1번 미분한다면 다음과 같다.

$\displaystyle {dM_x(t) \over dt} = 0 + E[X] + E[X^2]t + {1\over 2!}E[X^3]t^2 + \dots$

$t=0$을 대입해주면 결국 다음과 같이 E[X]만 남게 되고 결국 1차 미분하면 1차 적률이 구해진다.

$\displaystyle {dM_X(0) \over dt} = E[X]$

또 만약 2번 미분한다면 다음과 같다.

$\displaystyle {d^2M_X(t) \over dt^2} = E[X^2] + E[X^3]t + \dots$

또 $t=0$을 대입해주면 다음과 같이 2차 적률 $E[X^2]$을 구할 수 있게 된다.

$\displaystyle {d^2M_X(0) \over dt^2} = E[X^2] + E[X^3]t + \dots$

마지막으로 n번 미분한다면 다음과 같은 n차 적률을 구할 수 있게 되는 것이다.

$\displaystyle {d^nM_X(0) \over dt^n} = E[X^n]$

즉 요약하면 적률생성함수란 확률변수 $X$의 거듭제곱의 기대값을 구하는 함수이며, 적률생성함수를 한 번 구해두기만 하면 $n$번 미분하고 $t=0$을 대입해주면 쉽게 $n$차 적률을 구할 수 있다. 

적률추정법

적률의 배경과 의미와 정의부터 적률생성함수를 만들어 미분해서 $n$차 적률을 구해보았다. 그렇다면 이러한 적률은 어디에 쓰일까? 궁극적으로 적률은 적률추정법을 통해 모수를 추정하기 위해 사용한다. 적률추정법은 $n$차 모적률과 $n$차 표본적률을 일치시켜 모수를 추정하는 방법으로 최대가능도와 베이지안 추론과 같이 모수를 추정하는 점추정 방법에 속한다. 모수란 평균과 분산과 같은 모집단을 대표할 수 있는 값으로 보통 통계량 중 평균을 가장 많이 사용한다. 따라서 적률법이라고도 불리는 이 적률추정법은 표본평균을 통해 모평균과 일치하는 $\theta$를 찾는 방법이다. 평균이 아니여도 분산 등의 다른 통계량이 일치해도 된다. 하지만 일반적으로 확률분포에서 모수는 평균인 기대값 $\mu = E(x)$으로 표현한다. 예를 들어 모집단이 정규 분포를 따른다고 할 때 $N(\mu, \sigma^2)$로 표현하는 것과 같다. 

돌아와 적률추정법은 $n$차 모적률과 $n$차 표본적률을 일치 시켜 모수를 추정하는 방법이라 했다. 이를 수식으로 나타내면 $n$차 모적률 ($\displaystyle m_n = E[X^n]$)을 $n$차 표본 적률 ($\displaystyle \hat{m}_n = {1\over n}\sum_{i=1}^m X_i^n$)과 일치시켜 모수를 추정한다고 표현한다. 그리고 이 표본평균이 곧 모수 $\theta$에 대한 점추정 값이 된다. 

이러한 적률추정법은 점추정량을 구하는 가장 오래된 방법으로 최대가능도보다 자주 사용되진 않으나 손쉽게 계산 가능하다는 장점이 있다. 반면 비현실적인 추정량을 제시하는 경우가 있다는 단점이 존재한다. 이를 보완하기 위해 최대우도법(MLE), 베이즈 추정법 등을 사용한다.

덧붙여, 이 적률은 딥러닝에서 Adam Optimizer에 활용된다.

Reference

[1] 모멘트 & 모멘텀

[2] 모멘트( moment ) (lifeisforu)

[3] What Is Momentum?

[4] 적률법 (위키백과)

[5] 통계학 : 적률 (moment)

[6] Option Skew — Part 6: The Skewness and Kurtosis for a Lognormal (Roi Polanitzer)

[7] [확률과 통계] 45. 적률과 적률생성함수, Moment & Moment-Generating Function (mykepzzang)

[8] [통계 적률의 이해] 7. 적률생성함수 수학 거의 없이 이해하기 (통계의 본질)

[9] [통계학] 17. 추정법과 점추정량 - 적률법, 최대가능도추정법, 일치성, 비편향성, 효율성 (AI 꿈나무)

[10] [적률의 이해] 6. 적률생성함수란? (통계의 본질)

[11] Method of Estimation 추정법 (정보통신기술용어해설)

가설 검정이란?

가설 검정이란 어떤 추측이나 가설에 대해 타당성을 조사하는 것이다. 통계학에서 가설 검정은 표본통계량으로 모수를 추정할 때 추정한 모수값 또는 확률 분포 등이 얼마나 타당한지 평가하는 통계적 추론이다. 이 가설 검정에는 크게 귀무가설과 대립가설이 쓰인다. 귀무가설(null hypothesis)은 처음부터 버릴 것으로 예상하는 가설이며, 대립 가설(alternative hypothesis)은 귀무가설과 반대로 실제로 주장하거나 증명하고 싶은 가설이다.

가설 검정 단계는?

귀무가설과 대립가설을 통해 가설 검정을 진행하는 단계는 크게 4단계로 이루어진다. 

위 4단계의 과정을 제약회사의 신약 개발 예시를 들어 설명하면 다음과 같다.

1. 귀무가설과 대립가설을 수립한다.

귀무가설($H0$): 신약이 효과가 없을 것이다. 따라서 제약회사에 유의미한 수익 창출이 어려울 것이다.

대립가설($H1$): 신약이 효과가 있을 것이다. 따라서 제약회사에 유의미한 수익 창출이 가능할 것이다.

이 때 귀무 가설은 보통 $H0$로 표현하며 대립 가설은 $H1$로 표현한다. 두 가설들은 아래 단계들을 거쳐 하나가 채택된다. 

2. 유의수준(significant level, $\alpha$)을 설정한다. 

유의수준은 가설 예측을 100% 옳게 할 수 없으므로 오차를 고려하기 위한 것이다. 유의수준을 통해 귀무가설 채택여부 결정한다. 일반적으로 $\alpha = 0.05$로 설정하지만 검정 실시자의 결정에 따라 달라질 수 있다. 여기서 만약 $\alpha=0.05$로 설정한다면 이 값을 기준으로 귀무가설 또는 대립가설을 채택한다. 만약 이후 단계들로부터 검정 통계량을 기반으로 하는 p-value가 산출되었을 때 0.05보다 낮다면 귀무가설을 기각하고 대립가설을 채택한다. 

유의수준을 정할 때 함께 결정해야 하는 것은 양측 검정/단측 검정이다. 양측검정은 두 가설 모두에 관심 있을 때 사용하며 단측검정은 한 가설에만 관심 있을 때 사용한다. 예를 들어 제약회사 예시에서는 신약 효과가 있는지만 증명하면 자연스럽게 효과가 없음도 증명할 수 있으므로 단측 검정을 사용할 수 있다. 하지만 만약 남자와 여자의 스트레스의 차이를 두고 가설이 수립되었다면 양쪽 모두 살펴보아야 하므로 양측 검정을 사용해야 한다.

(* 유의수준과 함께 사용되는 기각역이라는 것은 단측 검정과 양측 검정에 위치하는 유의수준 $\alpha$ 크기에 해당하는 영역을 의미한다.)

3. 검정 통계량을 계산후 p-value를 도출한다. 

검정 통계량은 모수 추정을 위해 구하는 표본 통계량과 같은 의미를 가지는 것으로 가설 검정시 사용하는 표본 통계량을 뜻한다. 또 검정 통계량은 표본을 통해 가설 검정에 사용하는 확률 변수이다. 확률 변수라는 것은 그래프 상에서 x축을 나타내는 것이므로 확률 변수에 대한 확률 값을 나타내는 y값과는 다르다. 따라서 이 검정 통계량(확률 변수)은 확률분포 상에서 x축을 의미한다. 이 검정 통계량을 구하기 위해 사용하는 방법들은 아래와 같이 Z검정, T검정, 카이제곱 검정, F검정 등이 있다. 

이쯤에서 혼동되는 것은 검정이라 부르는것과 분포라 부르는 것은 어떤 차이를 가질까? 핵심은 내부적으로 사용하는 함수 식이 다르다. 예를 들어 검정에서 사용되는 함수는 검정력 함수라 부르는 것으로 확률분포의 x축 값을 검정력 함수에 넣어 검정 통계량을 구하는데 사용한다. 반면 분포는 x축과 함께 y축은 확률을 구해 확률분포로 나타낼 수 있는 식이다. 위의 그림에선 검정력 함수만 나타내고 있다.

이제 가설 검정의 핵심인 p-value(유의 확률)을 구하기 위해서는 위 검정력 함수를 통해 구한 검정 통계량을 알아야 한다. 예를 들어 아래와 같이 Z분포를 따르는 검정통계량이 있고 Z검정을 통해 어떤 한 표본의 검정통계량 z를 구했을 때 x축 위의 z지점까지의 누적분포함수가 곧 p-value가 된다.

4. p-value를 기준으로 귀무가설 채택 여부를 결정한다.

만약 위 그래프에서 검정 통계량 z가 기각역이라 불리는 유의수준 $\alpha$ 영역 내에 위치하게 된다면 귀무가설을 기각하고 대립가설을 채택하게 된다. 즉  p-value가 유의수준 $\alpha$보다 같거나 작다면 귀무가설을 기각하고, p-value가 유의수준 $\alpha$보다 크다면 귀무가설을 채택한다.

제약회사 예시에서 만약 신약 효과가 없을 확률이 유의수준($\alpha=0.05$)보다 작다면 효과가 없다는 귀무가설을 기각하고 효과가 있다는 대립가설을 채택하는 것이다. 반대로 만약 신약 효과가 없을 확률이 유의수준($\alpha=0.05$)보다 크다면 신약 효과가 없을 확률이 더 높은 것이므로 귀무가설을 채택하고 대립가설을 기각한다.

1종 오류와 2종 오류

1종 오류

쉽게 말해 1종 오류란 귀무가설이 참인데 기각한 경우를 말한다. 예를 들어 신약이 효과가 있어 제약회사에서 많은 수익을 벌었지만 알고보니 신약이 효과가 없었을 때를 의미한다. 즉 귀무가설을 기각하고 대립가설을 채택했지만 이것이 잘못된 검정이었음을 뜻한다. 이에 의거하면 p-value의 의미는 1종 오류를 얼마나 범할 확률을 나타내기도 한다. 즉 p-value가 5%라면 100번 검정하면 5번 정도 1종 오류가 발생하는 것이다. 또 이에 따라 유의 수준 $\alpha$는 1종 오류의 상한선이라고 말할 수 있다. 따라서 검정 결과 p-value가 $\alpha$보다 낮다면 상한선을 벗어나지 않으므로 이를 귀무가설을 기각하고 p-value가 $\alpha$보다 높다면 상한선을 벗어났으므로 귀무가설을 채택한다.

2종 오류

쉽게 말해 2종 오류란 귀무가설이 거짓인데 참으로 판단한 경우를 의미한다. 예를 들어 신약이 효과가 없다는 귀무가설이 사실로 밝혀져서 제약회사에서 생산과 판매를 그만두었지만 알고보니 효과가 있었을 때를 의미한다. 

Reference

[1] [개념 통계 21] 가설 검정 방법과 원리 - 필로홍

[2] 검정통계량이란? - 나부랭이의 수학블로그

[3] 가설검정 기본개념 완벽 이해하기

[4] Difference Between One-tailed and Two-tailed Test

빈도주의(Frequentism)와 베이즈주의(Baysianism)

통계학에서 확률을 해석하는 두 관점이 있다. 그 관점은 빈도주의와 베이즈주의다. 빈도주의는 연역적 추론에 해당하며 베이즈주의는 귀납적 추론에 해당한다. 이러한 빈도주의와 베이주주의는 상호보완 관계에 있다. 빈도주의는 확률을 사건의 빈도로 보며, 반대로 베이즈주의는 확률을 사건 발생에 대한 믿음/척도로 바라본다. 또 빈도주의는 모수를 정적으로 전제되어 있는 상수로 보며, 반대로 베이즈주의는 모수를 동적이며 불확실한 변수로로 본다. 

빈도주의는 사건을 여러 번 관측하여 발생한 확률을 검정하므로 사건이 독립성을 띤다는 장점이 있다. 예를 들어 동전 앞/뒷면을 여러 번 던져 관찰하게 되면 앞면도 0.5 뒷면도 0.5에 수렴하게 되며 앞면이 나올 확률이 0.5, 뒷면이 나올 확률이 0.5로 고정시킨다. 반면 베이지안주의는 동전이 앞면이 나왔다는 주장의 신뢰도가 50%다, 뒷면이 나왔다는 주장의 신뢰도가 50%라고 말한다. 빈도주의의 단점은 사건이 충분히 발생하지 못해 즉, 표본(데이터)이 부족할 경우 이러한 확률의 신뢰도가 떨어진다는 점이다.

베이즈주의는 이러한 빈도주의의 단점인 만약 여러 번의 사건을 관측할 수 없는 경우에 사용할 수 있다. 예를 들어 쓰나미의 예측 문제와 같다. 쓰나미가 발생하기 위해서는 여러 변수가 있다. 우선 지진이 발생해야하고 이로 인해 단층에 어긋남이 생기고 지형이 변화함에 따라 중력장이 발생할 때 주위로 퍼져나가면서 쓰나미가 된다. 이처럼 발생횟수가 적은 사건들에는 빈도주의를 적용할 수 없다. 다만 베이즈주의를 사용해 귀납적인 추론으로 쓰나미가 발생할 확률을 구할 수 있을 뿐이다. 본 글에서는 이러한 베이즈주의의 근간이 되는 베이즈 정리에 대해 정리하고자 한다.

베이즈 정리란?

베이즈 정리는 사전 확률(prior probability)과 사후 확률(posterior probability)의 관계를 나타내는 정리다. 이 베이즈 정리는 조건부 확률을 기반으로 한다. 조건부 확률이란 사건 $A$가 발생했다는 전제하에 사건 $B$가 일어날 확률이다. $P(B|A) = {P(B \cap A) \over P(A)}$로 표현한다. 베이즈 정리는 이 조건부 확률에서 유도된 것으로 다음과 같은 수식으로 나타낸다.

위 두 수식은 동일하게 베이즈 정리를 나타낸 것으로 변수명만 달리했다. 그 이유는 이해를 조금 더 쉽게 돕기 위함으로 왼쪽은 조건부 확률로부터 유도될 때 흔히 사용하고, 오른쪽은 베이즈 정리가 결국 모수($\theta$) 추정을 목적으로 한다는 것을 보이기 위함이다. 수식의 의미를 하나씩 분석해보자면, 먼저 posterior는 새로운 표본 X가 관측됐을 때 어떤 모수값을 갖는지를 의미한다. likelihood는 어떤 표본 X가 관찰되었을 때 어떤 확률분포를 갖는 모집단(모수)에서 추출되었을 확률을 의미한다. prior는 사전확률인 모수값을 의미하며, evidence는 모집단으로부터 표본 X가 관측될 확률이다. 결국 이 베이즈 정리를 요약하면 가능도(likelihood), 사전확률(prior), 관측 데이터(evidence)를 이용해 사후 확률(posterior)를 예측하는 방법이다.

베이즈 정리 유도

베이즈 정리를 유도하는 방법은 간단하다. 베이즈 정리 유도는 아래 식이 성립됨을 증명하는 것이다. 

$P(A|B) = {P(A \cap B) \over P(B)} = {P(B|A)P(A) \over P(B)}$

증명을 위해 조건부 확률 두 개를 구해준 다음 분모를 이항하고 양변을 나눠주면 된다. 앞서 조건부 확률은 $P(A|B) = {P(A\cap B) \over P(B)}$라고 했다. 이를 반대로 하면 $P(B|A) = {P(B\cap A) \over P(A)}$이다. 여기서 양변에 분모를 곱해주면 다음과 같은 형태가 된다. 

$P(A|B)P(B) = P(A\cap B)$

$P(B|A)P(A) = P(B\cap A)$

이 때, $P(A\cap B) = P(B\cap A)$이므로

$P(A|B)P(B) = P(B|A)P(A)$가 되고 여기서 양변을 $P(B)$로 나눠주면

$P(A|B) = {P(B|A)P(A) \over P(B)}$가 된다.

베이즈 정리 예시: 스팸 메일 확률 예측

스팸 메일 필터는 특정 단어 포함 여부를 기준으로 스팸 여부를 판단한다. 어떤 한 회사에 수신되는 메일 중 30%가 스팸메일이고 70%가 정상메일이다. 또 스팸메일 내용엔 A란 특정 단어가 포함될 확률이 40%고 정상 메일은 10%다. 이 때 A라는 단어가 보일 때 이 메일이 스팸메일일 확률은 얼마인가?

$P(S) = 0.3$ (스팸메일일 확률)

$P(N) = 0.7$ (정상메일일 확률)

$P(A|S) = 0.4$ (스팸메일에 A가 포함될 확률)

$P(A|N) = 0.1$ (정상메일에 A가 포함될 확률)

$P(A) = 0.19$ (A가 정상메일/스팸메일 모두 포함될 확률)

$P(A)$의 경우 스팸메일에 A가 포함될 확률 + 정상메일에 A가 포함될 확률이다. 두 사건은 상호배타적이므로 덧셈법칙을 사용해 계산할 수 있다. 즉 $P(A) = (P(A|S) * P(S)) + (P(A|N) * P(N))$이다. 이를 계산하면 $(0.4 * 0.3) + (0.1 * 0.7) = 0.19$이다. 즉 $P(A) = 0.19$다.

이렇게 사전 정보를 전부 구했으니 A라는 단어가 보일 때 스팸메일일 확률인 $P(A|S)$를 구해보자. $P(A|S) = {P(A\cap S) \over P(S)}$다. 여기서 이항해주면 $P(A|S)P(S) = P(A\cap S)$다. 이를 계산하면 $0.3 \times 0.4 = 0.12$다. 

$P(S|A) = {P(S\cap A) \over P(A)} = {0.12 \over 0.19} = 0.6315$

즉 사전 확률인, A라는 단어가 보일 때 해당 메일이 스팸메일일 확률이 0.6315가 된다. 

Reference

[1] https://ko.wikipedia.org/wiki/베이즈_추론

[2] https://brunch.co.kr/@aischool/3

[3] https://velog.io/@taeki531/베이지안베이즈-정리-유도

[4] https://deep-learning-study.tistory.com/44

누적분포함수란 확률론에서 주어진 확률분포가 특정 값보다 작거나 같은 확률을 나타내는 함수이다. 이 특정 값이라는 것은 어떤 사건을 의미하므로 누적분포함수는 어떤 사건이 얼마나 많이/적게 나타나는지에 관한 함수라고도 할 수 있다. 누적분포함수의 대표적인 특징은 확률변수가 이산형/연속형과 무관하게 모든 실수값을 출력한다는 것이다. 예를 들어 주사위를 던져 특정 값이 나올 확률변수 X의 값이 아래와 같이 1~6로 주어져 있다고 가정하자.

이 때 만약 확률변수 X가 2보다 같거나 낮은 수가 나타날 확률이 얼마일까? 고민할 것 없이 1, 2 두 가지 경우이므로 $2\over 6$이다. 그렇다면 만약 확률변수 X가 2.5보다 작거나 같은 경우와 같이 X가 실수 값을 가지는 경우는 어떻게 해야할까? 이 또한 마찬가지다. 확률변수는 이산 값만 갖고 있으므로 2.5보다 같거나 낮은 경우는 1, 2를 가질 경우이니 $2\over 6$다. 또 만약 확률변수 X가 10보다 작거나 같을 확률을 묻는다면? 1, 2, 3, 4, 5, 6 모든 경우가 해당하므로 ${6\over 6} = 1$이 된다. 이처럼 누적분포함수는 확률변수가 이산확률변수/연속확률변수와 무관하게 실수값을 입력으로 받을 수 있다. 이러한 누적분포함수를 수식으로는 다음과 같이 나타낸다.

$F(a) = P(X \leq a) = \sum_{x \leq a} p(x)$

수식을 세 부분으로 나누어 분석해보자면 왼쪽에 가까울수록 추상성을, 오른쪽으로 갈수록 구체성을 띤다. 가장 맨 왼쪽의 함수 $F$는 누적분포함수를 의미한다. 누적분포함수는 특정확률변수보다 같거나 작을 확률을 표현하는 함수이므로 특정확률변수로 $a$를 입력으로 한다. 가운데 식도 마찬가지다 어떤 사건에서 발생할 수 있는 여러 확률변수 중에서 $a$보다 작은 확률변수들의 확률값을 구하는 것이다. 오른쪽 식도 동일하다. $a$보다 작은 확률변수 x에 대해서 모든 합을 구해주는 것이다. 위 주사위 예를 들어 2.5보다 작을 확률이면 $a=2.5$가 되고 확률변수 x는 1,2를 가질 수 있으므로 위 식의 값은 $2\over 6$이 된다. 이러한 누적분포를 그래프로는 다음과 같이 표현할 수 있다.

위 그림에서 확인할 수 있듯 누적분포함수(CDF)는 확률밀도함수(PDF) 전체에 대한 부분을 표현하는 함수라고도 할 수 있다. PDF가 확률변수가 가질 수 있는 전체 확률 분포를 표현한 것이라면, CDF는 전체 확률 분포에서 확률변수가 $a$ 보다 작을 확률이다. 위 예시에서는 $a=1$보다 작을 확률이 되겠다. 이러한 확률밀도함수와 누적분포함수와의 관계를 다르게 말해서, 확률밀도함수를 적분하면 누적분포함수가 되며 또 반대로 누적분포함수를 미분하면 확률분포함수가 된다고 표현할 수 있다.

Reference

[1] https://www.youtube.com/watch?v=vMBxOtGhFQ0 

[2] https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jung1pp&logNo=221597577634 

[3] https://ko.wikipedia.org/wiki/누적_분포_함수

적분은 크게 부정적분과 정적분으로 나뉜다. 부정적분은 미분의 역연산이며, 정적분은 넓이/부피를 계산하는 방법이다. 실용적 관점에서 정적분이 많이 쓰이므로 적분은 대개 정적분을 의미한다. 부정적분과 정적분의 차이는 계산 형태와 적분상수 여부다. 부정적분은 대부분 답이 식으로 도출되며 정적분은 대부분 값으로 도출된다. 이는 부정적분은 $\int $처럼 정해진 구간이 없고 정적분은 $\int_a^b$처럼 정해진 구간이 있기 때문이다. 따라서 정해진 구간이 없는 부정적분은 적분상수가 있고, 정해진 구간이 있는 정적분은 적분상수가 계산 과정에서 사라진다. 이러한 부정적분과 정적분은 도출되는 형태는 다르지만 결국 공통적인 목표는 구간의 넓이/부피를 구하는 것이다. 

부정적분 (indefinite integral, 不定積分)

부정적분에서의 부정은 넓이/부피를 계산할 수 있는 적분 구간을 정할 수 없다는 의미다. 따라서 모든 구간에 대해 일반화를 통해 $f(x)$의 넓이가 이러할 것이라 표현할 수 밖에 없어 식의 형태로 도출된다. 만약 함수 $f(x)$의 부정적분을 $F(x)$로 둔다면 ${d\over dx}F(x) = f(x)$으로 표현할 수 있다. 부정적분은 정적분과 달리 식의 형태로 나타나고 적분상수가 있으므로, $\int f(x)dx = F(x) + C$로 표현할 수 있다. 이 때 $F(x)$를 $f(x)$의 원시함수라고도 부른다. 

정적분 (definite integral, 定積分)

정적분은 넓이와 부피를 계산할 수 있는 적분 구간이 정해져 있다는 의미다. 따라서 구간의 넓이가 계산되어 수치 형태로 도출된다. 부정적분이 가능한 모든 범위에 대한 일반화라면 정적분은 정해진 구간에 대한 특수화라 볼 수 있다. 정적분의 기호를 풀어 쓰면 $a$와 $b$ 구간에서 높이를 $f(x)$로 두고, 밑변(적분변수)을 $dx$로 두어 넓이를 계산하는 것이다. 참고로 정적분이 $\int_a^b f(x)dx = F(b) - F(a)$로 주어져 있다면 $\left[F(x)\right]_a^b$로도 표현할 수 있다. 그 이유는 정적분하는 과정에서 부정적분을 거치기 때문에 부정적분 식을 따로 쓰기 위한 목적이다. 

P.S 향후 필요의 경우 정적분의 종류인 중적분, 이상적분, 스틸체스 적분, 르베그 적분, 리만 적분 등에 대한 내용 추가 예정

Reference

[1] 적분 https://namu.wiki/w/%EC%A0%81%EB%B6%84

[2] 부정적분과 정적분 사이 관계 https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=piry777&logNo=100160884382

[3] 부정적분의 개념,미분과 부정적분과의 관계 https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=sbssbi69&logNo=90172290254

부분 적분은 미적분학에서 두 함수의 곱을 적분하는 기법이다. 치환 적분은 미적분학에서 기존 변수를 새로운 변수로 바꾸어 적분하는 기법이다. 부분 적분은 변수가 바뀌지 않으므로 적분 구간이 바뀌지 않지만, 치환 적분은 변수가 바뀌므로 적분 구간이 바뀐다. 부분 적분은 치환 적분이 적용되지 않을 때 사용한다. 

부분적분

부분적분에서는 두 함수를 $f(x)$와 $g(x)$로 두고 적분을 진행한다. 이 때 $f(x)$와 $g(x)$로 두는 함수의 기준이 존재한다. 그 기준은 미분의 용이성과 적분의 용이성이다. 일명 로다삼지로 알려져 있는데 로그함수, 다항함수, 삼각함수, 지수함수를 뜻한다. 만약 로그함수에 가깝다면 미분이 쉬우므로 $f(x)$로, 지수함수에 가깝다면 적분이 쉬우므로 $g(x)$로 두어야 한다. 이는 추후 계산의 용이성을 위함이다. 두 함수를 두는 방법의 예로, 로그함수와 삼각함수가 곱해진 경우라면 로그함수는 $f(x)$로 삼각함수는 $g(x)$로 둔다. 또 다항함수와 지수함수가 곱해진 경우라면 다항함수를 $f(x)$로 지수함수를 $g(x)$로 둔다. 로다삼지의 예시로 로그함수는 $logx$, $\ln x$를 말하고, 다항함수는 $n$차 다항식/일차함수/이차함수를 말한다. 또 삼각함수는 $sin$, $cos$, $tan$, $secx$, $cscx$, $cotx$를 말하고, 지수함수는 $n^x$, $e^x$를 말한다. (참고로 지수함수를 부정적분하는 공식은 $\int e^{f(x)}dx = {e^{f(x)} \over f'(x)} + C$다.)

그렇다면 부분적분의 공식은 무엇이고 어떻게 유도될까? 부분적분의 공식은 다음과 같다.

$\int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx$

이를 유도하는 과정은 매우 간단하다. 부분적분은 미분가능한 두 함수 $f(x)$, $g(x)$가 있을 때 두 함수의 곱인 $f(x)g(x)$를 미분한다. 미분한 결과는 $\{f(x)g(x)\}' = f'(x)g(x) + f(x)g'(x)$이다. 이 상태에서 다시 적분하면 $f(x)g(x)$가 되어야 할 것이다. 따라서 양변을 x에 대해 적분하면 $f(x)g(x) = \int f'(x)g(x)dx + \int f(x)g'(x)dx$가 된다. 이 때$\int f'(x)g(x)dx$를 이항하게 되면 위 공식이 된다.

그렇다면 3개의 예시를 통해 실제로 부분적분을 적용해보자. 만약 $\int xe^xdx$라면 미분이 쉬운 다항식인 $x$를 $f(x)$로, 적분이 쉬운 지수함수인 $e^x$를 $g'(x)$로 둔다. 부분적분 공식에 의해 $\int xe^xdx = xe^x - \int 1\times e^xdx$가 되므로 결과적으로 $xe^x-e^x+C$가 된다. $e^x$를 적분하면 $e^x$가 되므로. (+미분해도 $e^x$)

두 번째로 $\int \ln xdx$라면 $f(x)$를 $\ln x$로 $g'(x)$를 1로 둔다. 부분적분 공식에 의해 $\int \ln xdx = x\ln x - \int {1\over x}xdx$이다. 따라서 $\int \ln x = x\ln x - \int dx$가 되므로 결과는 $\int \ln x = x\ln x - x + C$가 된다.

세 번째로 $\int x\sin 2xdx$라면 $f(x)=x$로, $g'(x)=\sin 2x$로 둔다. 부분적분 공식에 의해 $\int x\sin 2xdx = x\times -{1\over 2}cos2x - \int 1\times -1{1\over 2}cos2xdx$가 되고 추가 계산하면 결과적으로 $\int x\sin 2xdx = -{1\over 2}xcos2x + {1\over}4\sin 2x + C$가 된다.

이러한 부분적분을 매우 쉽게할 수 있는 경우가 있다. 만약 계속 미분하면 0이되는 함수와 계속 적분할 수 있는 함수와의 곱이라면 가능하다. 아래 그림의 두 예시와 같은 과정으로 이뤄진다. 참고로 +와 -는 차례대로 번갈아가며 적용한다. 또 아래의 $g(x)$는 위의 $g'(x)$와 같다.

치환 적분

치환 적분은 복잡한 함성함수를 적분할 때 사용하는 방법으로 $ g(x) = t$ (이 때 g(x)는 미분가능 함수)와 같이 적분 변수($x$)를 다른 변수($t$)로 바꾸어 적분하는 방법이다. 예를 들어 $\int \cos(2x+1)dx$와 같은 함수를 적분해야 하는 상황에서 $2x+1 = t$와 같이 치환하여 단순화 시키는 것이다. 먼저 결론을 말하자면 치환 적분의 공식은 다음과 같다.

$\int f(x)dx = \int f(g(t))g'(t)dt$

그렇다면 이 치환 적분의 공식은 어떻게 유도될까? 간단하다. 먼저 $dy \over dx$는 $x$에 대한 $y$의 변화량이다. 하지만 이는 ${dy \over dx} = {dy \over dt} {dt \over dx}$로도 표현할 수 있다. 이후 $\int f(x)dx$라는 식이 있을 때 $x = g(t)$로 둔다. 이때 $x$를 미분하면 ${dx\over dt} = g'(t)$가 된다. 이를 기존의 식에 대입하면 $\int f(g(t))g'(t)dt$가 된다. 즉 $x$에 대한 적분을 $t$에 대한 적분으로 치환한 것이다.

이 치환 적분 공식을 2개의 예시에 적용해보자. 첫 번째로 $\int \cos (2x+1)dx$의 부정적분을 구해보자. 먼저 $2x+1 = t$로 둔다. 이후 양변을 $x$에 대해 미분하면 ${dt\over dx}=2$이므로, $dx={1\over 2}dt$가 된다. 따라서 이를 적분하고자 했던 식에 대입하면 $\int \cos t \times {1\over 2}dt$이 된다. 이제 이를 적분하면 ${1\over2} \sin t + C$의 형태가 되며 t에 대환 치환을 다시 $x$로 돌려주면 결과적으로 ${1\over 2}\sin (2x+1) +C$로 적분 계산 값이 도출된다.

두 번째 예시는 $\int x{\sqrt{x+1}}dx$이다. 마찬가지로 $x+1 = t$로 치환한다. $x$에 대해 미분하면 ${dt\over dx} = 1$이므로 $dt = dx$가 된다. 따라서 이를 대입해주면 $\int (t-1)\sqrt{t}dt$가 되고, 조금 난잡해보일 수 있지만 루트 표현식을 분수 표현식으로 바꾸면 $\int (t{3\over 2}-t{1\over 2})dt$가 된다. 이제 적분할 수 있다. 계산하면 ${2\over 5} t^2\sqrt{t} - {2\over 3}t\sqrt{t} +C$가 된다. $t$로 치환된 값을 다시 $x$로 풀어주면 결과적으로 ${2\over 5}(x+1)^2 \sqrt{x+1} - {2\over 3}(x+1)\sqrt{x+1} + C$로 적분 계산 값이 도출된다.

Reference

[1] 부분적분 쉽게하기 https://www.youtube.com/watch?v=E8N1E5ZAiIU 

[2] 부분적분, 치환적분 https://m.blog.naver.com/biomath2k/221860999596

[3] 치환적분 유도와 문제 예시 https://www.youtube.com/watch?v=SLnYC7mvyhk 

[4] 치환적분 문제 예시 https://blog.naver.com/biomath2k/221861047023

통계에서 확률변수와 확률분포가 있다. 확률변수는 이산확률변수와 연속확률변수로 나뉘고, 마찬가지로 확률분포도 이산확률분포와 연속확률분포로 나뉜다. 이산의 대표적인 분포는 이항분포가 있고 연속의 대표적인 분포는 정규분포가 있다. 하지만 이외에도 베르누이 분포, 기하분포, 초기하분포, 포아송분포, 균등분포, 지수분포, 카이제곱 분포 등이 있고 총 12가지 분포에 대해 정리하고자 한다. 이러한 확률 분포들이 필요한 핵심 이유는 모수 추정에 있다. 모수 추정에 있어 어떤 확률 분포를 따른다고 가정하면 특정 상황을 잘 표현할 수 있기 때문이다.

간단 용어 정리

표본공간: 사건에서 발생 가능한 모든 결과의 집합

확률변수: 표본공간에서 일정 확률을 갖고 발생하는 사건에 수치를 일대일 대응시키는 함수

확률분포: 흩어진 확률변수를 모아 함수 형태로 만든 것

이산확률변수: 확률변수 개수가 유한해 정수 구간으로 표현되는 확률변수

연속확률변수: 확률변수 개수가 무한해 실수 구간으로 표현되는 확률변수

확률밀도함수: 확률변수의 분포를 나타내는 함수이자 확률변수의 크기를 나타내는 값

이산 확률 분포

1. 베르누이 분포 (Bernoulli distribution)

베르누이 분포는 시행의 결과가 오직 두 가지인 분포를 말한다. 예를 들어 성공/실패나 합격/불합격 또는 앞면/뒷면이 있다. 이를 일반화하면 베르누이 분포는 특정 사건 A가 나타날 확률과 A가 나타나지 않을 확률을 나타낸 분포이다. 일반적으로 확률 변수에 사건 A가 발생할 경우를 1, 발생하지 않을 경우를 0으로 부여한다. 즉 베르누이 분포는 확률변수가 1과 0 두 가지로만 나타내는 확률분포다.

베르누이 시행을 따르는 경우의 예시로는, 동전과 주사위가 있다. 동전이 앞면이 나올 경우와 나오지 않을 경우로 나눌 수 있고, 주사위에서 어떤 수가 나올 확률과 그렇지 않은 경우로 나눌 수 있다. 만약 주사위에서 5가 나올 확률과 그렇지 않은 확률을 구하는 경우라면 베르누이 시행이지만 5,6이 나올 확률과 그렇지 않은 경우를 구하는 것이라면 베르누이 시행이 아니다. 예시를 통해 계산 방법을 알아보자. 상자 안에 흰 공7개와 검은공 3개가 있다고 가정하고 확률변수를 흰공이 나오면 성공(1), 검은공이 나오면 실패(0)로 둘때, 확률변수 값은 $p(1)=0.7, p(0)=0.3$이 된다. 이를 $\displaystyle p(x) = 0.7^x \times 0.3^{1-x}$로 나타낼 수 있고, 이를 일반화 한 식은 다음과 같다.

$\displaystyle p(x) = p^x(1-p)^{1-x}$

이 때 $x=(0, 1)$

다음으로 베르누이 분포에서 평균과 분산을 구하는 과정은 다음과 같다.

$\displaystyle E(x) = \sum xp(x)$

             $= 0p(0) + 1p(1)$

             $= p(1)$

             $= p$

$\displaystyle V(x) = E(x^2) - \{E(x)\}^2$

              $\displaystyle = \sum x^2p(x) - p^2$

              $= 0p(0) + 1p(1) - p^2$

              $= p - p^2$

              $= p(1-p)$

$\therefore$ $E(x) = p$, $V(x) = p(1-p)$이다.

2. 이항분포 (Binomial distribution)

이항 분포는 베르누이 시행을 여러번 하는 것이다. 정의를 내리면, 어떤 사건 A가 발생할 확률이 $p$인 베르누이 시행을 $n$번 시행했을 때 사건 A가 발생한 횟수를 확률 변수로하는 분포다. 수식으로는 다음과 같이 나타낸다.

$\displaystyle P(X = r) = {}_nC_r\ p^r(1-p)^{n-r} = {n \choose k}p^r(1-p)^{n-r}$

이 때 $r= (0, 1, 2, \dots, n)$이고 $(p+q = 1)$이다.

만약 주사위를 10번 던져서 숫자 5가 r번 나올 확률을 구한다면 다음과 같다.

만약 주사위 10번 던져서 숫자 5가 한 번 나올 확률: ${}_{10}C{}_1\times({1\over6})^1\times ({5\over 6})^9$

만약 주사위 10번 던져서 숫자 5가 두 번 나올 확률: ${}_{10}C{}_2\times({1\over6})^2\times ({5\over 6})^8$

만약 주사위 10번 던져서 숫자 5가 세 번 나올 확률: ${}_{10}C{}_3\times({1\over6})^3\times ({5\over 6})^7$

만약 주사위 10번 던져서 숫자 5가 r 번 나올 확률: ${}_{10}C{}_r\times({1\over6})^r\times ({5\over 6})^{n-r}$

이러한 사건의 시행으로부터 나오는 확률을 구해 분포도를 그리면 이항분포가 된다. 정확히는 확률변수 X의 확률분포를 이항분포라고 한다. 기호로는 $\displaystyle B(n, p)$와 같이 나타내며 위의 예시로는 $\displaystyle B(10, {1\over6})$이 된다. 만약 $X \sim B(n, p)$일 때 이항분포의 평균과 분산은 각각 $\displaystyle E(x) = np$ 이며 $\displaystyle V(x) = np(1-p)$이다. 평균을 구하는 과정만 기술해보자면,

$\displaystyle E(x) = \sum xp(x)$

              $\displaystyle = \sum_{r=0}^n r{n \choose r}p^r (1-p)^{n-r}$

              $\displaystyle = \sum_{r=0}^n r{n! \over (n-r)r!} p^r (1-p)^{n-r}$ (이 때 0을 대입하면 값이 0이되니 $r=1$부터 시작해도 되므로)

              $\displaystyle = \sum_{r=1}^n r{n! \over (n-r)r!} p^r (1-p)^{n-r}$ (약분을 위해 $r$을 묶어서 한 번 빼주고, $n$과 $p$도 마찬가지로 한 번씩 앞으로 빼주면)

              $\displaystyle = \sum_{r=1}^n r {n(n-1)! \over r(r-1)! (n-r)!} p p^{r-1} (1-p)^{n-r}$ (약분해주고 남은 np는 상수이며 앞으로 뺄 수 있으므로)

              $\displaystyle = np\sum_{r=1}^n {(n-1)! \over (r-1)!(n-r)!} p^{r-1} (1-p)^{n-r}$ ($n-1 = m$로 치환, $r-1 = x$로 치환하면)

              $\displaystyle = np\sum_{r=1}^n {m! \over x!(n-r)!} p^x (1-p)^{n-r}$ (이 때 $n-1 = m - x$이므로 대입해주면)

              $\displaystyle = np\sum_{r=1}^n {m! \over x!(m-x)!} p^x (1-p)^{m-x}$

              $\displaystyle = np\sum_{x=0}^m {m! \over x!(m-x)!}p^x (1-p)^{m-x}$ (이 때 $np$ 뒤의 형태는 시행횟수 m, 확률 p를 가지는 이항분포이므로 합은 1이 되어 사라지고)

              $= np$

$\therefore E(x) = np$

3. 기하분포 (Geometric distribution)

기하분포는 베르누이 시행을 반복할 때 처음으로 알고자 하는 사건 A 관찰에 성공하기 까지의 시도 횟수를 확률변수로 가지는 분포이다. 예를 들어 연애에서 결혼까지 이어질 확률이 10%라면 $x$번째 연애에 결혼하게 되는 것을 $p(x)$라 할 수 있다. 만약 3번째 연애에 결혼한다 가정하면 다음과 같은 계산이 가능하다.

$p(1) = 0.1$

$p(2) = 0.9 \times 0.1$

$p(3) = 0.9 \times 0.9 \times 0.1$

이를 일반화 하면 $\displaystyle p(x) = (1-p)^{x-1} \times p$이 된다. ($x$번째에 성공하므로 $x-1$까지는 실패)

이 기하분포의 통계량 중 평균과 분산은 $X \sim Geo(p)$일 때 $\displaystyle E(x) = {1\over p}, V(x) = {1-p\over p^2}$이다. 평균을 구하는 과정만 기술해보자면, 

$\displaystyle E(x) = \sum xp(x) = \sum x(1-p)^{x-1}p = \lim_{n \to \infty} \sum_{x=1}^n x(1-p)^{x-1}p$ (n이 무한히 커질 수 있음. p를 앞으로 꺼내주고 식을 전개하면)

$\displaystyle E(x) = \lim_{n \to \infty} p\{1(1-p)^0 + 2(1-p)^1+3(1-p)^2+ \cdots + (n-1)(1-p)^{n-2}+n(1-p)^{n-1}\}$ (평균값 도출 위해 양변에 (1-p)를 곱하면)

$\displaystyle (1-p)E(x) = \lim_{n \to \infty} p\{(1-p)+2(1-p)^2+3(1-p)^3+\cdots+(n-1)(1-p)^{n-1}+n(1-p)^n\}$ (위 식에서 이 식을 빼면)

$\displaystyle pE(x) = \lim_{n \to \infty} p\{1+(1-p)+(1-p)^2+(1-p)^3+\cdots+(1-p)^{n-1}+(1-p)^n\}$ (첫항1, 공비(1-p), 항수n인 등비수열합이므로)

$\displaystyle E(x) = \lim_{n \to \infty} \{{1(1-(1-p)^n \over1-(1-p)} - n(1-p)^n\}$ (로피탈 정리에 의해 0으로 수렴하는 $(1-p)^n$을 고려하면)

$\displaystyle E(x) = {1\over 1-(1-p)} = {1\over p}$

$\displaystyle \therefore E(x) = {1\over p}$

4. 음이항분포 (Negative binomial distribution)

음이항 분포의 여러 정의 중 하나는 기하 분포를 일반화한 분포다. 정확히는 음이항분포에는 5가지 정의가 존재하고 그 중 하나의 정의가 기하 분포의 일반화에 해당한다. 앞서 기하분포를 설명한 대로, $n$번째 시행에서 처음으로 사건 A 관측에 성공할 확률이다. 수식으론 $\displaystyle p(x) = (1-p)^{x-1} \times p$으로 표현했다. 음이항분포의 한 정의는 $n$번째 시행에서 $k$번째 성공이 나올 확률이다. 즉 $n$번 시행 이전인 $n-1$번의 시행까지 $k-1$개의 성공이 있어야 하며, 마지막 n번째에 한 번 더 성공해야 한다. 이를 수식으로 정의하면 $n-1$에서 $k-1$개가 나올 경우의 수를 고려해야 하므로 $\displaystyle p(x) = {}_{n-1}C_{k-1}p^{k-1}(1-p)^{n-k}p$가 된다.

앞서 언급했듯 음이항분포는 5가지 정의가 존재한다. 이 5가지 정의엔 $n, k, r$이 사용된다. $n$: 전체 시행횟수, $k$: 성공 횟수, $r$: 실패 횟수이다. 이 때 $n = k + r$의 관계가 성립한다. 이 관계식에서 어떤 것을 독립 변수, 종속변수, 상수로 두느냐에 따라 음이항분포의 정의가 나뉜다.

1. $r$이 상수, $k$가 독립변수인 경우: $r$번 실패까지 성공이 $k$번 발생한 확률이다.

2. $r$이 상수, $n$이 독립변수인 경우: $r$번 실패까지 $n$번 시행할 확률이다.

3. $k$가 상수, $r$이 독립변수인 경우: $k$번 성공까지 $r$번 실패할 확률이다.

4. $k$가 상수, $n$이 독립변수인 경우: $n$번 시행에서 $k$번째 성공이 나올 확률이다.

5. $n$이 상수, $k$ 또는 $r$이 독립변수인 경우: $n$번 시행에서 $k$번 성공 또는 $r$번 실패할 확률 (= 기존 이항분포와 동일한 식)

혼동이 있을 수 있지만 결론을 먼저 말하자면 일반적으로 1번 정의를 음이항분포라고 한다. 4번 정의는 기하분포를 일반화한 것이다. 1번 정의에 대한 예시를 들기 포커 게임에서 이길 확률(p) 0.3일 때 5번의 패배가 나오기까지 발생한 승리가 $k$번일 확률 분포 $p(x)$를 구한다고 해보자. 그러면 $r=5, p=0.3$이며 $x=(0, 1, 2, 3, 4, 5)$가 된다. 

p(0): 5번 패배할 때까지 0번 이긴 경우다.

(_ _ _ _ 실): 마지막 실패 제외, 모두 실패가 들어간다. 4번 중 4번 패배 + 0번 이길 경우의 수 이므로 ${}_4C_0 (0.7)^4 (0.3)^0 (0.7)$

p(1): 5번 패배할 때까지 1번 이긴 경우다.

(_ _ _ _ _ 실): 마지막 실패 제외, 5번 중 4번 패패 + 1번 이길 경우의 수 이므로 ${}_5C_1 (0.7)^4 (0.3)^1 (0.7)$

p(2): 5번 패배할 때 까지 2번 이긴 경우다.

(_ _ _ _ _ _ 실): 마지막 실패 제외, 6번 중 4번 패배 + 2번 이길 경우의 수이므로 ${}_6C_2 (0.7)^4 (0.3)^2 (0.7)$

p(3): 5번 패배할 때 까지 3번 이긴 경우다.

(_ _ _ _ _ _ _ 실): 마지막 실패 제외, 7번 중 4번 패패 + 3번 이길 경우의 수므로 ${}_7C_3 (0.7)^4 (0.3)^3 (0.7)$

. . . ($k \rightarrow \infty$)

이를 일반화한 수식은 ${}_{x+k-1}C_{x} (1-p)^r p^x$이 된다. 이를 달리 표현하면 $X \sim NB(r, p)$이다. 다른 정의를 사용하고 싶다면 $r$ 자리에 다른 상수를 넣어 사용할 수 있다. 이런 음이항분포의 평균과 분산은 각각 $\displaystyle E(x) = {pr \over 1-p}$와 $\displaystyle V(x) = {pr \over (1-p)^2}$이다. 이 중 평균을 구하는 과정만 기술하자면, 

$\displaystyle E(x) = \sum xp(x)$

              $\displaystyle = \sum_{x=0}^\infty x {}_{x+r-1}C_x p^x (1-p)^r$ ($x=0$은 0이므로 $x=1$부터여도 무관하며 조합식을 팩토리얼로 풀어주면)

              $\displaystyle = \sum_{x=1}^\infty x {(x+r-1)! \over (r-1)!x!} p^x (1-p)^r$ ($x$을 약분하면)

              $\displaystyle = \sum_{x=1}^\infty {(x+r-1)! \over (r-1)!(x-1)!} p^x (1-p)^r$ ($p$로 한 번 묶어주면)

              $\displaystyle = p \sum_{x=1}^\infty {(x+r-1)! \over (r-1)!(x-1)!} p^{x-1} (1-p)^r$ (분자 분모에 $r$을 곱해주면)

              $\displaystyle = p \sum_{x=1}^\infty {r(x+r-1)! \over r(r-1)!(x-1)!} p^{x-1} (1-p)^r$ ($r$을 앞으로 빼주고 팩토리얼을 합해주면)

              $\displaystyle = pr \sum_{x=1}^\infty {(x+r-1)! \over r!(x-1)!} p^{x-1} (1-p)^r$ ($x-1 = y$로 치환해주면)

              $\displaystyle = pr \sum_{y=0}^\infty {(y+r)! \over r!y!} p^y (1-p)^r$ (조합식으로 변경해주면)

              $\displaystyle = pr \sum_{y=0}^\infty {}_{y+r}C_y p^y (1-p)^r$ ($r = k-1$로 치환해주면)

              $\displaystyle = pr \sum_{y=0}^\infty {}_{y+k-1}C_y p^y (1-p)^{k-1}$ ($(1-p)^{-1})$으로 묶어주면)

              $\displaystyle = {pr \over 1-p} \sum_{y=0}^\infty {}_{y+k-1}C_y p^y (1-p)^k$ (이 때 시그마 안의 식은 음이항분포의 확률분포 함수와 모양이 같으므로 합은 1이 된다.)

              $\displaystyle = {pr \over 1-p}$

$\displaystyle \therefore E(x) = {pr \over 1-p}$

어떤 확률변수 $X$가 $NB(r, p)$의 음이항분포를 따를 때 이 확률변수 $X$의 평균은 $\displaystyle {pr \over 1-p}$가 된다.

5. 초기하 분포 (Hypergeometric distribution)

초기하 분포는 아래 그림처럼 크기가 $m$인 모집단에서 크기 $n$인 표본을 추출했을 때 모집단 내 원하는 원소 $k$개 중 표본 내에 $x$개 들어있을 확률 분포를 의미한다.

쉬운 비유는 로또가 있다. 로또는 크기 45의 모집단을 가지고, 그 중 원하는 수 $k=6$개이다. 이 때 추출한 표본 6개 중 $k$가 $x$개 들어있을 확률이다. 따라서 $p(0)$는 번호 0개 맞은 경우이며 $p(1)$은 번호 1개가 맞은 경우이고, ..., $p(6)$는 번호 6개가 맞아 1등된 확률을 의미한다. 

이러한 초기하 분포식 유도를 위해선 먼저 모집단에서 표본을 추출할 경우의 수를 구해야 한다. 이는 크기 $m$인 모집단에서 크기 $n$인 표본을 뽑을 경우의 수 이므로 ${}_mC_n$이다. 또 원하는 원소가 $k$개 들어있고 크기가 m인 모집단에서, 크기가 $n$인 표본을 뽑을 때 원하는 원소 x개가 들어있을 경우의 수는 ${}_kC_x \times {}_{m-k}C_{n-x}$다. 그 이유는 표본의 $x$이외의 값은 $n-x$개로 나타내며 이는 모집단의 $m-k$개로부터 추출된 것이기 때문이다. 이를 기반으로 전체 경우의수를 나타내면 다음과 같다.

$\displaystyle p(x) = {{}_kCx \times {}_{m-k}C_{n-x} \over {}_mCn}$

여기서 $m, k, n$은 사전에 결정되는 상수이며 $x$는 확률 변수에 해당한다. 이 초기하 분포식을 기반으로 구한 평균과 분산은 각각 $\displaystyle E(x) = {kn \over m}$, $\displaystyle V(x) = n {k\over m}{m-k \over m}{m-n\over m-1}$이다. 평균을 구하는 과정만 기술해보자면, 

$\displaystyle E(x) = \sum xp(x)$

              $\displaystyle = \sum_{x=0}^\infty {{}_kCx \times {}_{m-k}C_{n-x} \over {}_mCn}$ (이 때 ${}_kCx$를 팩토리얼로 풀어주면)

              $\displaystyle = \sum_{x=0}^\infty x{k! \over x!(k-x)!} {{}_{m-k}C_{n-x} \over {}_mC_n}$ (이 때 0을 대입하면 0이므로 x=1부터 시작되어도 무관. x 약분 하고 k를 밖으로 꺼내주면)

              $\displaystyle = k\sum_{x=1}^\infty {(k-1)! \over (x-1)!(k-x)!} {{}_{m-k}C_{n-x} \over {}_mC_n}$ (여기서 ${}_mC_n$을 팩토리얼로 전개하면 ${}_mC_n = {m! \over n!(m-n)!} = {m \over n}{(m-1)! \over (n-1)!(m-1)!} = {m\over n}{}_{m-1}C_{n-1}$)

              $\displaystyle = k\sum_{x=1}^\infty {(k-1)! \over (x-1)!(k-x)!} {n\over m} {{}_{m-k}C_{n-x} \over {}_{m-1}C_{n-1}}$ (여기서 맨 앞의 식을 조합 형태로 변환)

              $\displaystyle = k\sum_{x=1}^\infty {}_{k-1}C_{x-1} {n\over m} {{}_{m-k}C_{n-x} \over {}_{m-1}C_{n-1}}$ (여기서 $n\over m$은 상수이므로 앞으로 빼고 ${}_{m-k}C_{n-x}$를 변형하면)

              $\displaystyle = {kn\over m} \sum_{x=1}^\infty {}_{k-1}C_{x-1} {{}_{(m-1)-(k-1)}C_{(n-1)-(x-1)} \over {}_{m-1}C_{n-1}}$ (여기서 $x-1=y$로 치환하면)

              $\displaystyle = {kn\over m} \sum_{y=0}^\infty {}_{k-1}C_y {{}_{(m-1)-(k-1)}C_{(n-1)-(y)} \over {}_{m-1}C_{n-1}}$ (시그마 내 식은 크기 $m-1$인 모집단, $n-1$인 표본, 원하는 원소 $k-1$개, 원하는 원소 $y$인 초기하 분포의 모양과 같으므로 시그마 식은 초기하 분포 값을 다 더해주면 1)

              $\displaystyle = {kn\over m}$

$\displaystyle \therefore E(x) = {kn \over m}$

6. 포아송 분포 (Poisson distribution)

포아송 분포는 이항 분포에서 유도된 특수한 분포다. 이항 분포에서 시행 횟수 $n$이 무수히 커지고 사건 발생 확률 $p$이 매우 작아질 경우 필요하다. 그 이유는 시행 횟수 $n$이 무한히 커질 때 이항 분포 정의인 $\displaystyle {}_nC_r\ p^r(1-p)^{n-r}$에서 $n!$ 계산이 현실적으로 가능하지 않은 경우가 있기 때문이다.

포아송 분포를 다르게 표현하면 단위 시간이나 단위 공간에서 랜덤하게 발생하는 사건 발생횟수에 적용되는 분포다. 예를 들어 1시간 내에 특정 진도 5이상의 지진 발생 확률에도 적용할 수 있다. 지진은 언제나 발생할 수 있지만 그 발생횟수는 작을 것이며 또 알 수 없다. 또 보험사는 1000건의 보험계약이 있지만 고객이 보험금을 청구 확률은 얼마가 될 지 알 수 없는 것이다.

이러한 경우에 포아송 분포가 사용되며 많은 경우에 적용된다. 포아송 분포에서는 사건발생 횟수와 확률은 알 수 없지만 대신 사건발생 평균횟수는 정의할 수 있다. 그 이유는 이항 분포에서 평균 $E(x) = np$이기 때문이다. 푸아송 분포에서는 $np$를  $\lambda$로 표현한다. ($\lambda = np$)

포아송 분포의 정의는 이항 분포 정의에서 유도되어 $\displaystyle p(x) = {\lambda^x e^{-\lambda} \over x!}$이다. 이를 사용해 포아송 분포의 평균과 분산을 구하면 각각 $E(x) = \lambda$와 $V(x) = \lambda$이다. 이 때 평균을 구하는 과정만 기술해보자면,

$\displaystyle E(x) = \sum_{x=0}^\infty\ xp(x)$ 이므로

              $\displaystyle =\sum_{x=0}^\infty x {\lambda^x e^{-\lambda} \over x!}$ (이 때 $x$에 0대입해도 0이므로 1부터 시작 가능)

              $\displaystyle =\sum_{x=1}^\infty x {\lambda^x e^{-\lambda} \over x!}$ ($x$ 약분하고, 상수인 $e^{-\lambda}$를 앞으로 빼주고, $\lambda$도 하나 앞으로 빼주면)

              $\displaystyle =\lambda e^{-\lambda} \sum_{x=1}^\infty {\lambda^{x-1} \over (x-1)!}$ ($x-1 = n$으로 치환. $x=1$이면 $n=0$이므로)

              $\displaystyle =\lambda e^{-\lambda} \sum_{n=0}^\infty {\lambda^{n} \over n!}$ (이 때 시그마 값은 매클로린 급수 정의에 의해 $e^\lambda$. ($\displaystyle f(x) = \sum_{n=0}^\infty {f^{(n)}(0) \over n!} {x}^n$에서 $e^\lambda$대입. $e^x$의 $n$계 도함수는 자기 자신))

              $\displaystyle = \lambda e^{-\lambda} e^\lambda$

              $\displaystyle = \lambda$

$\displaystyle \therefore E(x) = \lambda$

연속확률분포

7. 균등분포 (Uniform distribution) 

균등분포의 정의는 정해진 범위에서 모든 확률변수의 함수값이 동일한 분포이다. 연속확률분포에서 균등분포는 연속균등분포라 불려야 한다. 이산확률분포에서도 균등분포를 정의할 수 있기 때문에 구분이 필요하기 때문이다. 균등분포 함수로 표현하면 다음과 같다.

$\displaystyle f(x)= \begin{cases} {1 \over b-a}, & a\lt x \lt b \\ 0 & {x\lt a, b\lt x} \end{cases}$

확률변수의 범위를 $a\leq x \leq b$라고 하고, 이 확률변수들의 함수 값을 $f(x)$라고 하면다음과 같은 확률밀도 그래프를 그릴 수 있다. 참고로 어떤 확률변수 $X$가 균등분포를 따른다면 $X~ U(a, b)$로 표현한다.

이 때 연속확률변수에서의 확률은 확률밀도로 표현되고 확률밀도는 넓이를 의미한다. 이 때 전체 확률밀도는 1이므로 $(b-a)f(x) = 1$이 된다. 따라서 $f(x) = {1 \over (b-a)}$이다. 

균등분포에서 평균과 분산은 각각 $\displaystyle E(x) = {b+a \over 2}$와 $\displaystyle V(x) = {(b-a)^2 \over 12}$이다. 여기서 평균을 나타내는 과정만 기술해보자면, 연속확률변수에서 평균은 $\displaystyle E(x) = \int_{-\infty}^\infty xf(x)dx$이므로

$\displaystyle E(x) = \int_a^b x{1 \over b-a}dx$

              $\displaystyle =\left[{1\over b-a} {1\over 2}x^2 \right]_a^b$

              $\displaystyle ={b^2-a^2 \over 2(b-a)}$

              $\displaystyle = {(b+a)(b-a) \over 2(b-a)}$

              $\displaystyle = {b+a \over 2}$

$\displaystyle \therefore E(x) = {b+a \over 2}$

8. 정규분포 (Normal distribution)

정규분포는 대표적인 연속확률분포에 속하며 가우시안 분포라고도 불린다. 정규분포의 확률밀도함수는 아래의 수식으로 나타낸다. (유도과정은 크게 두 가지 방법을 사용하는데 첫 번째론 과녁 맞추기 예시를 통한 유도와 두 번째론 이항분포로부터 유도하는 방법이 있다. 유도과정은 길어지므로 생략하며 고등수학만 활용해도 유도 가능하다.)

$\displaystyle f(x) = {1 \over \sqrt{2\pi \sigma^2}} \exp (-{(x-\mu)^2 \over 2\sigma^2})$

여기서 $\mu$는 평균을 나타내며 $\sigma^2$는 분산(표준편차 제곱)을 뜻한다. 이는 곧 정규분포는 아래 그림과 같이 평균과 분산에 따라 다양한 분포를 가지게 됨을 의미한다. 이 때 정규분포의 가장 높은 함수값을 가지는 확률변수 $X$는 평균이다. 만약 어떤 확률변수 $X$가 평균이 $\mu$고 분산이 $\sigma^2$인 정규분포를 따른다고 하면 기호로 $N(\mu, \sigma^2)$와 같은 형태로도 나타낼 수 있다. 

이러한 정규분포에는 몇 가지 특징이 있다. 첫 번째는 정규분포는 확률밀도함수의 한 종류이므로 전체 넓이는 전체 확률을 의미하므로 1이 된다. 두 번째는 정규분포는 평균을 기준으로 대칭성을 띤다. 평균 기준 왼쪽과 오른쪽이 각각 0.5의 확률을 갖는다. 세 번째는 정규분포별 평균과 표준편차가 다르더라도 아래 그림과 같이 표준편차 구간 별 확률은 어느 정규분포에서나 같다는 것이다. 

가령 예를 들어 $\displaystyle N(100, 5^2)$의 정규분포와 $\displaystyle N(64, 4^2)$ 정규분포가 두 개가 있을 때, 그 모양이 서로 다르더라도 위 그림과 같이 표준편차($\sigma$)로 나뉘어진 구간의 면적(확률)은 모두 같음을 의미한다. 

이런 정규분포는 표준화 과정을 통해 표준 정규 분포(standard normal distribution)를 얻을 수 있다. 표준 정규 분포란 평균이 0 표준편차가 1인 분포를 말한다. 표준화 과정은 $\displaystyle Z = {X - \mu \over \sigma}$으로 이뤄진다. 모든 확률변수에 대해 평균을 뺀 뒤 표준편차로 나눠주는 것이다. $Z \sim N(0, 1)$의 형태로 표현하며 이를 표준정규분포 또는 Z-분포라 부른다.

이런 표준화 과정을 통해 표준정규분포로 만들면 서로 다른 모수 값(평균, 표준편차, 분산 등)을 가진 정규분포를 가진 집단 간의 비교 문제를 해결할 수 있다. 흔히 예를 드는 것으로 수학 시험 점수 비교다. 가령 A, B반의 수학 점수가 정규분포를 따른다 가정할 때 A반: 평균 70, 표준편차 30 / B반: 평균 80, 표준편차 15라면 비교로 성적 우위를 가리기 어렵다. 때문에 표준화를 통해 정규분포를 표준정규분포로 바꿔줌으로써 집단간 비교 문제를 해결할 수 있다.

9. 카이제곱분포 (Chi-square distribution)

카이제곱분포란 표준정규분포에서 파생된 것으로 한 마디로 말하면 표준정규분포의 확률변수를 제곱합한 분포다. 카이제곱 분포는 신뢰구간과 가설검정, 독립성 검정 등에서 자주 사용된다. 먼저 카이제곱분포의 기본적인 형태를 보자. 표준정규분포에서는 평균이 0이고 표준편차가 1이었다. 따라서 평균 0을 기준으로 -와 +가 있지만 카이제곱분포는 확률변수를 제곱하였으므로 +만 존재한다. 

카이제곱분포의 형태에서 앞 부분에 확률 변수 값이 큰 이유는 뒤로갈수록 정규분포의 양끝과 같은 편향이 상대적으로 적어지기 때문이다. 이 카이제곱 분포를 조금 더 덧붙여 설명하면, $k$개의 서로 독립적인 표준정규분포의 확률변수를 각각 제곱한 후 더하여 얻는 분포다. 이 때 $k$는 표준정규분포를 따르는 확률변수의 개수로 카이제곱 분포의 형태를 결정하는 자유도로서 역할을 한다. 이 $k$에 따라 카이제곱 분포의 형태가 아래와 같이 달라진다. 자유도의 크기가 증가할수록 점점 대칭성을 갖게 되며 통상 $k=30$이상이면 거의 정규분포에 가까워진다고 한다. 

이러한 카이제곱분포의 수식은 $\displaystyle f(x|k) = {1 \over 2^{k\over 2}\gamma ({k\over 2})} x^{{k\over 2}-1}e^{-{x\over 2}}$로 표기한다. 카이제곱분포의 평균과 분산은 각각 $E(x) = k$, $V(x) = 2k$이다. 이 중 카이제곱분포 수식을 통해 평균을 구하는 과정만 기술해보자면, (확률변수 $X$가 $k$ 자유도를 갖는 카이제곱분포를 따른다고 가정)

$\displaystyle E(x) = \int_0^\infty xf(x)dx$ (적분구간은 0부터 시작함 카이제곱분포는 표준정규분포의 확률분포를 제곱한 것이므로)

              $\displaystyle =\int_0^\infty x{1\over 2^{k\over2} \gamma({k\over 2})} e^{-{x\over 2}} x^{{k\over 2}-1}dx$ (이 때 $x*x^{-1} = 1$이 되고, 상수를 앞으로 빼주면)

              $\displaystyle ={1 \over {2^{k\over 2} \gamma({k\over 2})}} \int_0^\infty e^{-{x\over 2}} x^{x\over 2} dx$ (여기서 부분적분을 적용하면)

              $\displaystyle ={1 \over {2^{k\over 2} \gamma({k\over 2})}} \left\{ \left[-2e^{-{x\over 2}} x^{x\over 2} \right ]_0^\infty - \int _0^\infty -2e^{-{x\over 2}} {k\over 2}x^{{k\over 2}-1}dx \right\}$

              $\displaystyle ={1 \over {2^{k\over 2} \gamma({k\over 2})}} \left\{ \left[-2e^{-{x\over 2}} x^{x\over 2} \right ]_0^\infty +k \int _0^\infty e^{-{x\over 2}} x^{{k\over 2}-1}dx \right\}$ (이 때 부분적분한 앞 항은 로피탈 정리에 의해 0으로 수렴됨)

              $\displaystyle ={1 \over {2^{k\over 2} \gamma({k\over 2})}} \left\{k \int _0^\infty e^{-{x\over 2}} x^{{k\over 2}-1}dx \right\}$ (앞의 항을 다시 적분식으로 넣어주면)

              $\displaystyle =k\int_0^\infty {1\over {2^{k\over 2} \gamma({k\over 2})}} e^{-{x\over 2}} x^{{k\over 2}-1}dx$ (여기서 적분식은 k자유도를 갖는 카이제곱분포함수와 동일하므로 적분 시 1이 됨)

              $\displaystyle =k$

$\displaystyle \therefore E(x) = k$ (어떤 확률변수 $X$가 $Q \sim \chi_k^2$의 카이제곱분포($k$ 자유도 갖는)를 따를 때 이 확률변수 $X$의 평균은 $k$다)

10. 지수분포 (Exponential distribution)

지수분포는 포아송 분포에서 유도된다. 위에서 포아송 분포는 단위 시간당 사건의 평균 발생 횟수였다. 수식으로는 $\displaystyle p(x) = {\lambda^x e^{-\lambda} \over x!}$였다. 여기서 $\lambda$는 단위 시간당 사건의 평균발생횟수($\because \lambda=np$)이며 $x$는 사건 발생 횟수이다. 예를 들어 하루 동안 모범 택시를 평균적으로 3번 마주친다면 $\displaystyle p(x) = {3^xe^{-3} \over x!}$이 된다.

지수분포는 이러한 포아송 분포가 만족하는 상황에서 사건 A가 일어날 때까지 걸리는 시간이 T이하일 확률이다. 즉 기존 포아송에서 시간까지 더 알고자 하는 것이다. 이를 일반화한 정의는 단위 시간당 사건 A의 평균발생횟수가 $\lambda$일 때, 사건 A가 처음 발생할 때 까지 걸리는 시간이 T이하일 확률이다. 지수 분포는 아래 수식으로 표현한다.

$\displaystyle f(T) = \lambda e^{-\lambda T}$

위 지수 분포 유도를 위해 하나의 예를 들어 설명 하자면, 모범 택시를 마주칠 때 까지 걸리는 기간이 5일 이하일 확률을 $\displaystyle p(0\leq t \leq 5) = \int_0^5 f(t)dt$로 표현할 수 있다. 이 확률을 구하기 위해서는 두 가지 방법이 있다. 첫 번째는 1일차에 만날 확률, 2일차에 만날 확률, ..., 5일차에 만날 확률을 구해 모두 더해주는 방식이고, 두 번째는 여사건을 사용하는 방법이다. 여사건을 통해 확률을 구하는 식은 (1 - 5일동안 모범 택시 마주치지 않을 확률 p)이다. 

여사건으로 계산을 해보자면 먼저 1일차에 모범택시를 만나지 않을 확률을 구하면 $\displaystyle p(0) = {3^0e^{-3} \over 0!} = e^{-3}$이 된다. 따라서 5일동안 모범 택시를 마주치지 않을 확률은 $\displaystyle e^{{-3}\times 5}$가 된다. 이 모범 택시를 마주칠 확률은 곧 $\displaystyle \int_0^5 f(t)dt = 1 - e^{-15}$와 같다.

이렇게 구한 포아송 분포를 지수분포로 일반화 하여 어떤 사건이 발생할 때 까지 걸리는 기간이 T이하일 확률을 나타내는 과정을 나타내보자. 우선 $\displaystyle p(0\leq t\leq T) = \int_0^T f(t)dt = 1 - e^{-\lambda T}$이 있고, 여기서 구해야할 것은 지수분포를 나타내는 $\displaystyle \int_0^T f(t)dt$이다. 지수분포 식은 T로 미분해서 얻을 수 있다. $f(t)$의 부정적분을 $F(T)$로 두면, 이 적분식은 $\displaystyle F(T) - F(0) = 1-e^{-\lambda T}$가 된다. 이 식의 양변을 T로 미분하면 $\displaystyle f(T) = \lambda e^{-\lambda T}$가 되며 이 함수는 지수분포를 나타내는 식이다.

이 지수함수 분포에 대한 평균과 를 이용해 평균과 분산은 각각 $\displaystyle E(x)={1 \over \lambda}$, $\displaystyle V(x)={1\over \lambda^2}$이다. 이 중 평균을 구하는 과정만 기술해보자면,

$\displaystyle E(t) = \int_0^\infty tf(t)dt$

              $\displaystyle = \int_0^\infty t \lambda e^{-\lambda t}dt$ (여기서 부분적분을 사용하면)

              $\displaystyle = \left[ -te^{-\lambda t} \right]_0^\infty - \int_0^\infty -e^{-\lambda t}dt$ ($\because \int e^{f(x)} = {e^{f(x)} \over f'(x)}$이며 부분적분 공식에 의해 $\int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)$이므로)

              $\displaystyle = \left[ -te^{-\lambda t}\right]_0^\infty + \left[-{1\over \lambda}e^{-\lambda t}\right]_0^\infty$ (이 식은 위 식에서 뒤 항을 적분해준 결과임. 여기서 극한값을 이용해 표현하면)

              $\displaystyle = \lim_{t \to \infty} (-te^{-\lambda t}) - 0 + \lim_{t \to \infty} -{1\over \lambda} e^{-\lambda t} - (- {1\over \lambda}e^0)$ (이 때 $\lim_{t \to \infty} -{1\over \lambda}e^{-\lambda t}$는 0이 되므로)

              $\displaystyle = \lim_{t \to \infty} (-te^{-\lambda t}) + {1\over \lambda}$ (여기서 -를 앞으로 빼고 지수 표현식을 분수로 바꿔주면)

              $\displaystyle = -\lim_{t \to \infty} {t \over e^{\lambda t}} + {1\over \lambda}$ (여기서 $1 = {1 \over \lambda } \lambda$이므로 이를 추가해주면)

              $\displaystyle = -{1 \over \lambda} \lim_{t \to \infty} {\lambda t \over e^{\lambda t}} + {1\over \lambda}$ (이 때 로피탈 정리에 의해 $\displaystyle \lim_{t \to \infty} {\lambda t \over e^{\lambda t}}$는 0이 됨)

              $\displaystyle = {1\over \lambda}$

$\displaystyle \therefore E(t) = {1 \over \lambda}$

11. 감마분포 (Gamma distribution)

감마분포는 지수분포의 확장이다. 지수분포에서 한 번의 사건이 아닌 여러 개의 사건으로 확장한 것이다. 구체적으론 지수분포는 포아송 분포가 만족하는 상황에서 사건 A가 일어날 때까지 걸리는 시간이 T이하일 확률이었다. 감마분포는 $\alpha$번째 사건이 발생할때까지 걸리는 시간이 T이하일 확률이다. 예를 들어 평균적으로 주유소를 30분에 한 번씩 마주친다면 주유소를 4번 마주칠 때까지 걸리는 시간이 T이하일 확률과 같은 것이다. 감마분포 또한 여러 곳에 활용되지만 주로 감마분포는 모수의 베이지안 추정에 활용된다.

감마함수는 $\displaystyle \gamma(\alpha) = \int_0^\infty x^{\alpha-1}e^{-x}dx, (\alpha \gt 0)$로 표기한다. 이 감마함수는 팩토리얼 계산을 자연수에서 복소수범위까지 일반화한 함수라고 한다. 이 감마 함수를 근간으로한 감마분포함수는 $\displaystyle f_x(x) = {1 \over \gamma(\alpha)\beta^\alpha} x^{\alpha-1}e^{-x\over \beta}$로 표기한다. ($\displaystyle 0 \leq x \leq \infty$, ($\alpha \gt 0, \beta \gt 0)$). 감마분포에서 $\alpha$는 형태 모수(shape parameter), $\beta$는 척도 모수(scale parameter)라고 한다.

감마분포의 평균과 분산은 각각 $E(x)=\alpha \beta$, $V(x) = \alpha \beta^2$이다. 여기서 감마분포의 평균을 구하는 과정만 기술하자면, 

$\displaystyle E(x) = \int_0^\infty xf(x)dx$

              $\displaystyle = \int_0^\infty  x{1 \over \gamma(\alpha)\beta^\alpha} x^{\alpha-1}e^{-x\over \beta}dx$ ($xx^{-1}=1$, 상수 부분을 앞으로 빼주면)

              $\displaystyle = {1 \over \gamma(\alpha) \beta^\alpha} \int_0^\infty x^\alpha e^{-{x\over \beta}}dx$ (${x\over \beta} = t$로 치환)

              $\displaystyle = {1 \over \gamma(\alpha) \beta^\alpha} \int_0^\infty (t\beta)^\alpha e^{-t} \beta dt$ ($\beta^\alpha$는 약분되어 사라지고 상수 $\beta$를 앞으로 빼주면)

              $\displaystyle = {\beta \over \gamma(\alpha)} \int_0^\infty t^\alpha e^{-t}dt$ (이 때 $\gamma$ 함수의 원형과 동일하므로)

              $\displaystyle = \beta {\gamma(\alpha+1) \over \gamma(\alpha)}$ ($\gamma$ 함수는 팩토리얼이므로 $\alpha$만 남게 됨)

              $\displaystyle = \beta \alpha$

$\displaystyle \therefore E(x) = \alpha \beta$

12. 베타분포 (Beta distribution)

베타분포는 베이즈 추론에서 사전 확률을 가정할 때 사용되기 때문에 중요하다. 베타분포의 정의는 두 매개변수 $\alpha$와 $\beta$에 따라 [0, 1] 구간에서 정의되는 연속확률분포이다. $\alpha$와 $\beta$는 아래와 같이 베타분포 그래프의 형태를 결정하는 형태 모수(shape parameter)다. 만약 $\alpha = \beta$라면 베타분포는 대칭이 된다. 또 $\alpha$와 $\beta$가 커질수록 정규분포와 모양이 비슷해진다. 

베타분포의 근간인 베타함수의 수식은 $\displaystyle B(\alpha, \beta) = {\gamma (\alpha) \gamma(\beta) \over \gamma(\alpha + \beta)} = \int_0^1 x^{\alpha -1}(1-x)^{\beta -1}dx$로 표현한다. 이 베타함수를 기반으로하는 베타분포의 확률밀도함수는 $\displaystyle f_x(x) = {\gamma(\alpha + \beta) \over \gamma(\alpha) \gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}, (0 \lt x \lt 1, \alpha, \beta \gt 0)$이다. 평균과 분산은 각각 $\displaystyle E(x) = {\alpha \over \alpha + \beta}$, $\displaystyle V(x) = {\alpha \beta \over (\alpha+\beta)^2(\alpha+\beta+1)}$인데, 이 중 평균을 구하는 과정만 기술하면,

$\displaystyle E(x) = \int_0^1 xf(x)dx$ 

              $\displaystyle =\int_0^1 x{1\over B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta-1}dx$

              $\displaystyle ={B(\alpha+1, \beta) \over B(\alpha, \beta)} \int_0^1 {1 \over B(\alpha+1, \beta)} x^{(\alpha+1)-1}(1-x)^{\beta-1}dx$

              $\displaystyle ={\gamma(\alpha+\beta) \over \gamma(\alpha)\gamma(\beta)} {\gamma(\alpha+1)\gamma(\beta) \over \gamma(\alpha+\beta+1)}$

              $\displaystyle = {\alpha \over \alpha+\beta}$

$\displaystyle \therefore E(x) = {\alpha \over \alpha+\beta}$

Reference

[1] 베르누이분포 https://www.youtube.com/watch?v=3rOIcMF0-ls 

[2] 이항분포 https://www.youtube.com/watch?v=XzJkxIkP4Pg 

[3] 기하분포 https://www.youtube.com/watch?v=NzQRbVP5eow 

[4] 기하 분포 https://blog.naver.com/PostView.naver?blogId=chunsa0127&logNo=222049190534 

[5] 음이항 분포 https://www.youtube.com/watch?v=bBo7rN3SvCg 

[6] 초기하 분포 https://www.youtube.com/watch?v=HT1en9f2AcE 

[7] 포아송 분포 https://www.youtube.com/watch?v=JOWYEDwqAtY 

[8] 균등 분포 https://www.youtube.com/watch?v=LeUfJHzOSXo 

[9] 정규 분포 https://m.blog.naver.com/algosn/221308973343

[10] 카이제곱 분포 https://math100.tistory.com/44

[11] 카이제곱 분포 https://www.youtube.com/watch?v=2ER99k6f5eQ 

[12] 지수 분포 https://www.youtube.com/watch?v=OywjNb4jmtc 

[13] 감마 분포 https://soohee410.github.io/gamma_dist

[14] 베타 분포 https://soohee410.github.io/beta_dist

[15] 이미지 https://quantitative-probabilitydistribution.blogspot.com/2021/01/various-types-of-probability.html