마르코프 체인 정의
마르코프 체인(Markov Chain)은 마르코프 성질을 지닌 이산확률과정이다. 마르코프 성질이란 $n+1$회의 상태(state)는 $n$회의 상태나 그 이전 $n-1, n-2, \dots$의 상태에 의해 결정되는 것이다. 달리 말해 과거 상태가 현재/미래 상태에 영향을 미치는 성질이다. 이산확률과정이란 시간의 진행에 대해 확률적인 변화를 가지는 구조를 의미한다. 이 마르코프 체인은 때때로 단순하지만 강력한 효과를 발휘하기에 사용한다. 실제로 예측을 위해선 많은 변수과 모델링을 거쳐야 하지만 마르코프 체인은 이런 비용을 줄여주기 때문이다.
마르코프 체인 예시
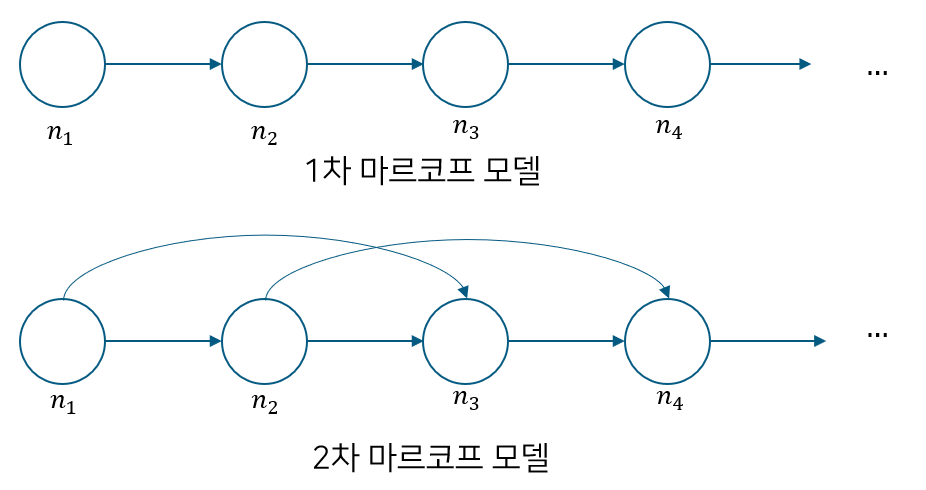
마르코프 성질 여부에 대한 흔한 예시로는 동전 앞뒤 예측과 날씨예측이 있다. 동전 앞뒤를 예측하는 것은 독립시행이기 때문에 n번째 상태가 n+1번째 상태에 영향을 주지 않으므로 마르코프 성질이 없다. 반면 날씨 예측과 같이 직관적으로 오늘 날씨에 의해 내일 날씨가 결정될 수 있으므로 마르코프 성질이 있다고 할 수 있다. 만약 오늘을 기반으로 하루 뒤를 예측한다면 1차 마코프 모델이라하고 이틀 뒤를 예측한다면 2차 마코프 모델이라 한다.
마르코프 체인 활용
마르코프 체인은 주로 결합확률분포(Joint Probability Distribution)에 사용된다. 예를 들어 확률 변수 $X_1, X_2, \dots, X_n$이 있다고 가정하면 일반적으로 이 확률변수들의 결합확률분포는 다음과 같이 계산할 수 있다.
$P(X_1, X_2, \dots, X_n) = P(X_1) \times P(X_2|X_1) \times P(X_3|X_2,X_1) \times \dots \times P(X_n|X_{n-1}, X_{n-2}, \dots, X_1)$
하지만 마르코프 성질을 이용하면 위 보다 더 단순한 계산을 통해 결합확률분포를 구할 수 있다.
만약 어떠한 상태의 시점이 $t$고, 확률분포가 마르코프 성질을 따른다면
$P(X_{t+1}|X_t, X_{t-1}, \dots, X_2, X_1) = P(X_{t+1}|X_t)$
로 단순화 할 수 있고 일반화를 적용하면 이전에 결합확률분포의 계산을 다음과 같이 단순화 가능하다.
$P(X_1, X_2, \dots, X_n) = P(X_1) \times P(X_2|X_1) \times P(X_3|X_2) \times P(X_4|X_3) \times \dots \times P(X_n|X_{n-1})$
이러한 마르코프 체인은 주로 베이지안 통계학이나 강화학습에 사용되며, MCMC(Markov Chain Monte Carlo)와도 연결되어 사용된다.
마르코프 모델
마르코프 모델이란 마르코프 체인을 기반으로 만든 확률 모델이다. 아래 날씨 예제를 통해 내일 날씨를 예측하는 마르코프 모델을 만들어보자. 마르코프 모델을 만들기 위해선 가장 먼저 각 상태를 정의해야 한다. 그리고 이 상태는 상태 전이 확률로 나타낸다. 상태 전이 확률이란 어떤 상태에서 다른 상태로 이동할 확률을 의미한다. 상태 전이 확률을 행렬로 표현한 것을 전이 행렬(Transition Matrix)라고 한다.

이 전이 행렬을 해석하자면 만약 오늘 날씨가 Sunny라면 내일 Suuny일 확률이 0.7, Rainy일 확률이 0.2, Cloudy일 확률이 0.1이라 예측한다. 이를 기반으로 오늘이 어떤 특정 날씨일 때 내일이 어떤 특정 날씨일 확률을 구하기 위해서는 위 전이 행렬이 $T$라고할 때 $T \times T$처럼 곱해주면 된다. 만약 오늘 날씨를 기반으로 이틀 뒤 날씨를 예측하고 싶다면 $T \times T \times T$를 계산하면 된다. 이렇게 반복적으로 전이행렬을 곱해줌으로써 일련의 예측을 함께 연결한다면 이를 마르코프 체인이라 한다.
참고로 전이 행렬을 거듭 곱하다보면 더 이상 전이 행렬의 값이 변하지 않고 수렴하는 상태가 오는데 이를 안정 상태(Steady State)라고 한다. 즉 행렬 $T$는 거듭곱해 어떤 행렬 $M$이 되지만 수렴한 뒤에는 $MT = T$가 된다. 또 전이 행렬은 도식화 가능하다. 이 도식화한 것을 상태 전이도(State Transition Diagram)라고 하며 아래와 같다.

전이 행렬 또는 상태 전이도를 기반으로 마르코프 모델을 만들어 날씨 예측을 할 수 있다. 아래는 10일간 날씨 예측을 할 수 있는 간단한 파이썬 스크립트다.
import numpy as np
transition_matrix = np.atleast_2d([[0.7, 0.2, 0.1],
[0.1, 0.6, 0.3],
[0.2, 0.5, 0.3]])
possible_states = ["sunny", "rainy", "cloudy"]
start_state = "sunny"
num = 10
index_dict = {}
future_state = []
for index in range(len(possible_states)): # {'sunny': 0, 'rainy': 1, 'cloudy': 2}
index_dict[possible_states[index]] = index
for _ in range(num):
new_state = np.random.choice(possible_states, p=transition_matrix[index_dict[start_state], :])
future_state.append(new_state)
print (future_state)
"""
> ['rainy', 'sunny', 'rainy', 'sunny', 'sunny', 'rainy', 'cloudy', 'sunny', 'sunny', 'sunny']
It will be different whenever you run it. because I used np.random.choice
"""
용어 정리
마르코프 체인(Markov Chain): 상태 전이 확률을 기반으로 일련의 예측을 연결한 것
마르코프 성질(Markov Property): $n+1$ state는 $n$ state에 의해 결정되는 것처럼 상태들 간의 인과성이 있는 성질
이산확률 과정(Discrete Stochastic Process): 시간 흐름에 따라 확률적인 변화를 가지는 구조. 특히 시간 흐름이 이산적일때를 의미
연속확률 과정(Continous Stochastic Process): 시간 흐름에 따라 확률적인 변화를 가지는 구조. 특히 시간 흐름이 연속적일 때를 의미
마르코프 모델(Markov Model): 미래 상태에 대한 확률 값이 과거에만 종속된 모델
상태 전이 확률(State Transition Probability): 어떤 상태에서 다른 상태로 이동할 확률
전이 행렬(Transition Matrix): 전이 확률을 행렬 형태로 나타낸 것
상태 전이도(State Transition Diagram): 상태 전이 확률을 정리하여 만든 도식
안정 상태(Steady State): 전이 행렬을 거듭 곱해도 더 이상 변하지 않는 상태
정적분포(Stationary Distribution): 전이 행렬이 안정 상태일 때 갖는 확률분포
상태 공간(State Space): $0, 1, 2, \dots, n-1, n$ 시점에서의 확률과정의 상태들의 집합
Reference
[1] Markov Chains
[2] Markov Chain Text Generation – Part 1 (KEN GRAHAM)
[3] 마르코프 체인 (Markov Chain) 정의 및 예시 (Data to Impact)
'Artificial Intelligence > 확률-통계학' 카테고리의 다른 글
| [확률/통계] KL Divergence, Cross Entropy, Entropy (0) | 2022.10.27 |
|---|---|
| [확률/통계] 회귀분석과 상관분석이란? (Regression Analysis and Correlation Analysis) (0) | 2022.10.24 |
| [확률/통계] 모수적 방법과 비모수적 방법 (parametric and non parametric) (0) | 2022.10.23 |
| [확률/통계] 적률추정법 이해하기 (Method of Moments Estimator) (0) | 2022.10.23 |
| [확률/통계] 가설 검정 이해하기 (귀무가설, 대립가설) (0) | 2022.10.21 |