For a better world

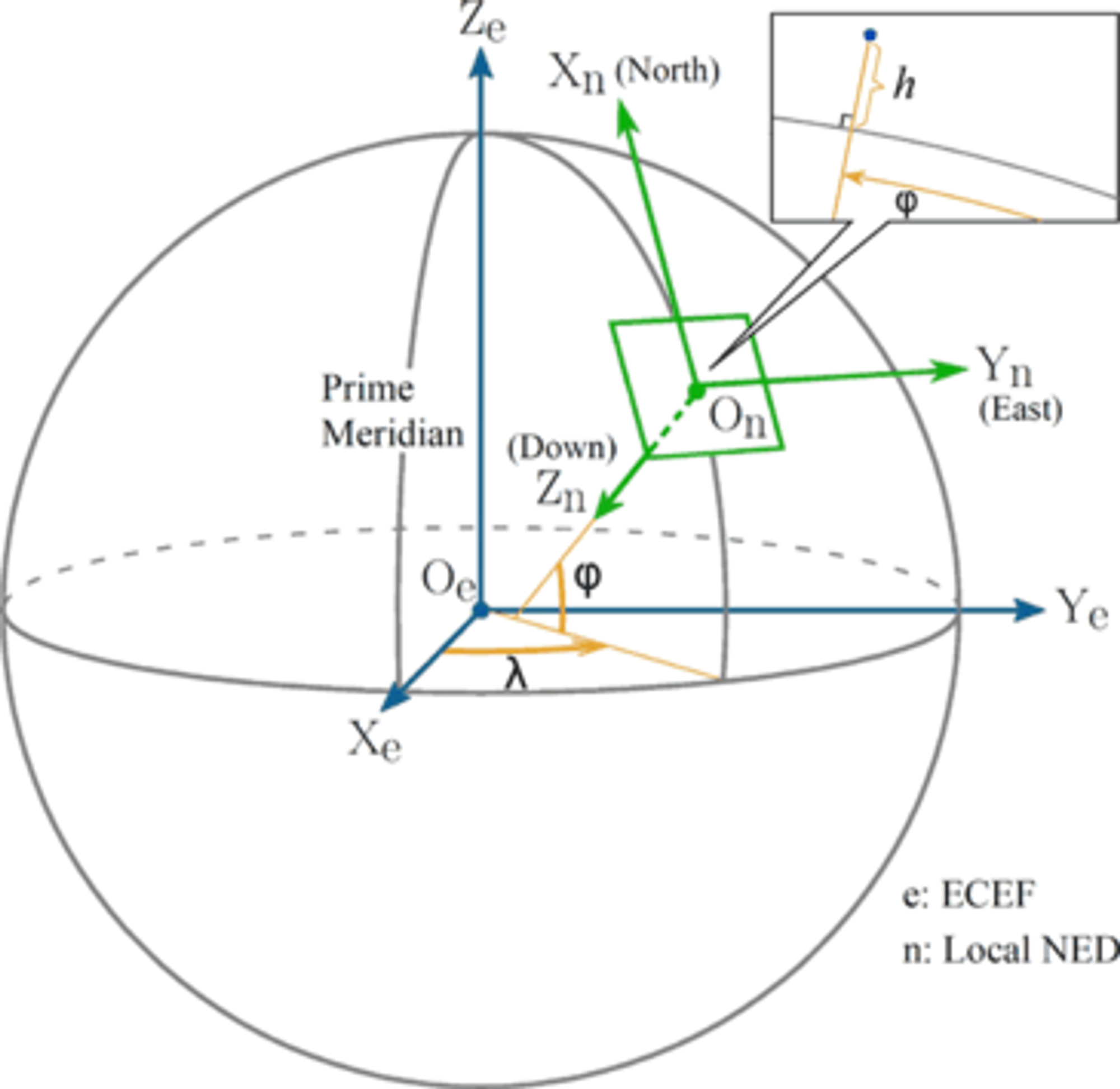
아래 내용은 <비행동역학 및 제어> 서적을 기반으로 작성되었습니다.

1.1 비행동역학 (Flight Dynamics)

비행동역학이란?

- 배경: 1903년 12월 라이트형제의 인류 최초 동력비행

- 개념: 대기를 비행하는 물체의 동적특성을 해석하는 학문

- 필요성: 좋은 성능의 비행제어시스템 설계를 위해

- 연관학문: 공기역학, 동역학, 구조역학, 수치해석학 등

1.2 비행제어: 유도항법제어

제어시스템 관련 요소

- 항법(Navigation): 비행체의 위치를 알아내는 것

- 유도(Guidance): 임무수행을 위한 위치이동을 위한 힘을 계산하는 것

- 제어(Control): 계산된 유도명령을 따르기 위해 비행체를 조절하는 것

2.1 비행동역학개론

- 항공기의 동적특성은 주로 안정성(Stability)과 조종성(Control)에 의해 규정됨

- 항공기의 동적특성에 직접적인 영향을 주는 것은 공력계수며 이를 이해하려면 에어포일과 날개의 기하학적, 공기역학적 특성을 살펴봐야함

- 시스템을 해석에는 주파수영역 해석기법이 있고 시간영역 해석기법이 있음

2.2 항공기의 기하학적, 공기역학적 특성

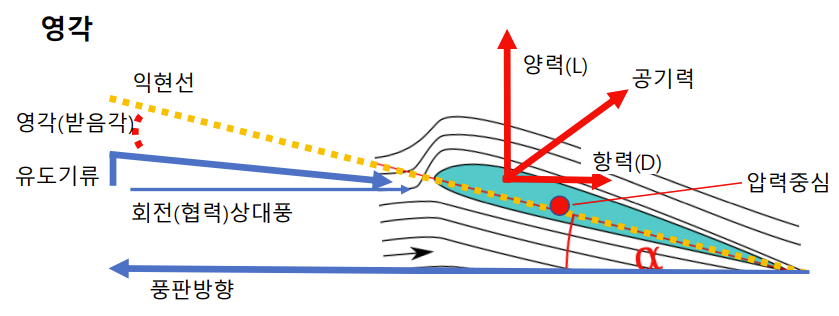
- 에어포일: 항공기 날개의 2차원 단면

- 날개: 2차원 모양의 에어포일을 날개 길이 방향으로 유한한 길이를 갖도록 포개서 만든 3차원 모형

- 양력발생원리: 에어포일 주변에 받음각으로 인해 에어포일 윗면과 아랫면의 유속차의 발생에 따라 압력분포가 달리 작용해 양력을 얻음

- 압력중심: 압력분포에 의한 모멘트 합이 0이 되는 점. 특징으론 받음각이 변하면 압력분포가 달라지므로 압력중심 위치도 변함

- 공력중심: 항공기 무게 중심에 대한 힘과 모멘트 계산에 있어 압력중심을 기준으로 사용하면 받음각의 변화로 압력중심이 달라지는 문제를 해결하기 위해 받음각에 따라 위치가 변하지 않는 점인 공력중심을 사용. 

- 피칭 모멘트(pitching moment): 모멘트가 Y축으로 작용(회전)하려는 힘

모멘트(Moment): 물체의 회전운동에 대한 양을 나타내는 개념이다. 즉 물체가 회전력을 받는 정도를 뜻한다. 모멘트는 어떤 물리량과 어떤 기준점 사이의 거리를 곱한 형태로 정의된다. 예를 들어 물리량은 질량, 힘, 길이 등이 될 수 있고 (질량 x 거리), (힘 x 거리), (길이 x 거리) 등으로 표현할 수 있다. 실제로 관성 모멘트는 질량과 거리제곱의 곱으로 표현되고 힘의 모멘트(토크)는 힘과 거리의 곱으로 표현된다. 모멘트는 어떤 물리량의 분포에 따라 물리적 특성이 달라질 때 사용한다.

2.4 비행안전성 개요

- 항공기 운동은 크게 병진운동과 회전운동으로 구분되며 이 둘은 서로 독립이라 가정해 별도의 해석이 필요함.

- 병진운동: 물체를 하나의 질점으로 간주해 질점계의 모든 질점이 평행이동 즉 모든 지점이 똑같이 이동하는 운동. 

- 회전운동: 물체가 한 점을 축으로 회전하는 운동. 주로 자세안정성해석이나 제어시스템 설계에 이용됨. 정적안정성과 동적안정성으로 구분됨. 정적안정성이란 크게 3가지로 정의됨. 한 물체가 초기에 평형상태에 있다고 가정했을 때 외력이 발생했지만 평형상태로 되돌아 가려는 1. 정적 안정, 외력이 발생해서 평형상태에서 멀어지는 2. 정적불안정, 평형이 유지되는 3. 정적중립. 동적안정성은 시간에 대한 변화를 염두에 두고 정의되는 특성으로 평형상태를 벗어난 뒤 어느 정도의 시간이 경과한 후 다시 평형상태로 되돌아오는 경향으로 정의

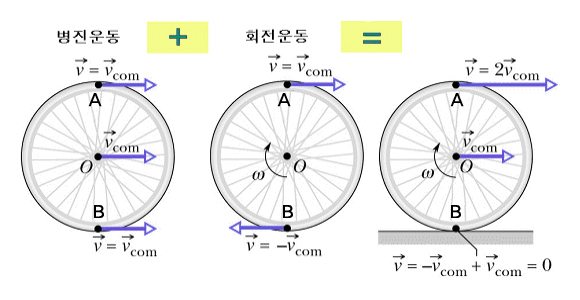
강체: 물리학에서 형태가 변하지 않는 물체. 외력이 가해져도 크기나 모양이 변형되지 않거나 무시할 만큼의 변형이라면 강체라 함. 강체의 가장 일반적인 운동은 질량중심의 병진운동과 질량중심을 지나는 축에 대한 회전운동의 결합.

(추가 작성 예정)

Reference

[1] <비행동역학 및 제어>

[2] https://dronelife.co.kr/oralexamination/?mod=document&uid=2085 

[3] https://astro.kasi.re.kr/learning/pageView/5231

항공 및 우주분야에서는 비행체의 상태를 표현하거나 위치, 속도, 고도 등의 항법연산을 위해 다양한 기준 좌표계가 사용된다. 대표적인 좌표계는 크게 4가지가 있다.

1. 지구중심 관성 좌표계 (ECI: Earth Centered Inertial reference frame)

지구중심 관성 좌표계란 관성의 법칙이 적용되는 좌표계다. 관성의 법칙이란 뉴턴의 운동법칙 제1법칙으로 물체에 아무런 힘이 가해지지 않을 경우 물체는 정지하거나 등속직선운동을 하는 것이다. 즉 시간의 변화에 따라 가속하거나 회전하지 않는 좌표계다. 실제로는 지구가 회전하고 있기 때문에 존재하지 않는 좌표지만 다른 좌표계들과의 관계를 기술하기 위한 목적으로 만든 가상의 좌표계다. 이러한 관성 좌표계와 달리 가속운동을 하는 좌표계를 비관성 좌표계 또는 가속 좌표계라 부른다.

2. 지구중심 지구고정 좌표계 (ECEF, Earth Centered Earth Fixed frame)

지구중심 지구고정 좌표계란 회전이 포함된 지구중심 관성 좌표계다. 즉 지구의 자전으로 인해 회전하는 좌표계며 t=0 시점에서 지구중심 관성 좌표계와 동일하다.

3. 지면좌표계 (NED: North East Down frame)

지면 좌표계(NED frame)는 항공 및 우주분야에서 널리 사용되는 좌표계다. LLA(Latitude-Longitude-Altitude) 좌표계라고도 불리는 NED 좌표계는 비행체의 상대적인 위치와 방향을 표현하기 위해 사용된다. N은 North, E는 East, D는 Down을 나타낸다. North는 경도선과 평행을 이루며 북쪽을 바라보는 방향을 표현한다. 적도를 기준으로 북반구는 + 남반구는 -이다. x, y, z를 기준으로 상대적인 좌표를 표현하는 local frame 좌표계에서의 x축과 같다. East는 위도선과 평행을 이루며 동쪽은 + 서쪽은 -로 방향을 표현한다. 마찬가지로 local frame 좌표계에서 y축과 같다. Down(Depth)은 지구 중심, 내부를 바라보는 방향을 표현하는 것으로 지구 중심과 가까워지는 방향은 + 중심과 멀어지는 방향은 -로 표현한다. 마찬가지로 local frame 좌표계에서 z축과 같다.

이러한 NED 좌표계는 일반적으로 3차원 직교 좌표계로 표현된다. (North, East, Down)이며 예를 들어 (100, 200, -50)은 북쪽으로 100 단위, 동쪽으로 200단위 아래로 50단위로 이동한 지점을 나타낸다. NED 좌표계는 항공 및 우주 분야에서 좌표와 방향을 정확하게 표현하는데 사용되는 다른 좌표계와 결합되어 사용될 수 있다. 예컨데 GPS 좌표는 NED 좌표계로 변환되어 위치를 정확하게 나타낼 수 있다.

4. 동체 좌표계 (Body frame)

동체 좌표계는 물체(ex: 비행체, 선박 등)의 질량 중심을 원점으로 하는 좌표계다. 물체의 운동을 설명하는데 사용하는 좌표계로 일반적으로 물체의 운동방정식을 동체 좌표계상에서 표현하기 대문에 운동 방정식을 전개해 나가는데 편리한 좌표계다. 동체 좌표계는 물체의 중심에 대한 위치와 물체의 방향을 기준으로 한다. 위치는 일반적으로 (x, y, z)로 표현되고 방향은 (roll, pitch, yaw)의 각도로 표현된다.

동체 좌표계는 무언가 오일러 좌표계와 관계가 있고 비슷해 보인다. 어떤 관계를 가지고 어떻게 다를까? 결론적으로 동체 좌표계 안에 오일러 좌표계가 부분집합으로 속해있는 형태다. 그 이유는 동체 좌표계는 대상체의 위치와 방향을 나타내는 반면 오일로 좌표계는 대상체의 방향을 나타내기 때문이다. 오일러 좌표는 물체의 방향(자세)를 설명하기 위해 사용하는 좌표계로 세 개의 연속된 회전 각도를 사용해 물체의 자세를 나타낸다. 일반적으로 (roll, pitch, yaw)로 회전을 나타내며 이는 곧 물체의 방향과 같다. 따라서 오일러 좌표계는 동체 좌표계의 방향 정보를 나타내기 위해 사용될 수 있다.

Reference

[1] https://saack.tistory.com/96

[2] https://dongmin-archive.tistory.com/entry/1-Reference-Coordinate-System-and-Transformations