[미적분학] 부정적분과 정적분 이해하기

적분은 크게 부정적분과 정적분으로 나뉜다. 부정적분은 미분의 역연산이며, 정적분은 넓이/부피를 계산하는 방법이다. 실용적 관점에서 정적분이 많이 쓰이므로 적분은 대개 정적분을 의미한다. 부정적분과 정적분의 차이는 계산 형태와 적분상수 여부다. 부정적분은 대부분 답이 식으로 도출되며 정적분은 대부분 값으로 도출된다. 이는 부정적분은 $\int $처럼 정해진 구간이 없고 정적분은 $\int_a^b$처럼 정해진 구간이 있기 때문이다. 따라서 정해진 구간이 없는 부정적분은 적분상수가 있고, 정해진 구간이 있는 정적분은 적분상수가 계산 과정에서 사라진다. 이러한 부정적분과 정적분은 도출되는 형태는 다르지만 결국 공통적인 목표는 구간의 넓이/부피를 구하는 것이다. 

 

 

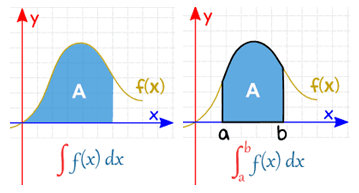
부정적분 (indefinite integral, 不定積分)

부정적분에서의 부정은 넓이/부피를 계산할 수 있는 적분 구간을 정할 수 없다는 의미다. 따라서 모든 구간에 대해 일반화를 통해 $f(x)$의 넓이가 이러할 것이라 표현할 수 밖에 없어 식의 형태로 도출된다. 만약 함수 $f(x)$의 부정적분을 $F(x)$로 둔다면 ${d\over dx}F(x) = f(x)$으로 표현할 수 있다. 부정적분은 정적분과 달리 식의 형태로 나타나고 적분상수가 있으므로, $\int f(x)dx = F(x) + C$로 표현할 수 있다. 이 때 $F(x)$를 $f(x)$의 원시함수라고도 부른다. 

 

정적분 (definite integral, 定積分)

정적분은 넓이와 부피를 계산할 수 있는 적분 구간이 정해져 있다는 의미다. 따라서 구간의 넓이가 계산되어 수치 형태로 도출된다. 부정적분이 가능한 모든 범위에 대한 일반화라면 정적분은 정해진 구간에 대한 특수화라 볼 수 있다. 정적분의 기호를 풀어 쓰면 $a$와 $b$ 구간에서 높이를 $f(x)$로 두고, 밑변(적분변수)을 $dx$로 두어 넓이를 계산하는 것이다. 참고로 정적분이 $\int_a^b f(x)dx = F(b) - F(a)$로 주어져 있다면 $\left[F(x)\right]_a^b$로도 표현할 수 있다. 그 이유는 정적분하는 과정에서 부정적분을 거치기 때문에 부정적분 식을 따로 쓰기 위한 목적이다. 

 

P.S 향후 필요의 경우 정적분의 종류인 중적분, 이상적분, 스틸체스 적분, 르베그 적분, 리만 적분 등에 대한 내용 추가 예정

 

Reference

[1] 적분 https://namu.wiki/w/%EC%A0%81%EB%B6%84

[2] 부정적분과 정적분 사이 관계 https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=piry777&logNo=100160884382

[3] 부정적분의 개념,미분과 부정적분과의 관계 https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=sbssbi69&logNo=90172290254