[미적분학] 부분 적분과 치환 적분 이해하기

 

부분 적분은 미적분학에서 두 함수의 곱을 적분하는 기법이다. 치환 적분은 미적분학에서 기존 변수를 새로운 변수로 바꾸어 적분하는 기법이다. 부분 적분은 변수가 바뀌지 않으므로 적분 구간이 바뀌지 않지만, 치환 적분은 변수가 바뀌므로 적분 구간이 바뀐다. 부분 적분은 치환 적분이 적용되지 않을 때 사용한다. 

 

부분적분

부분적분에서는 두 함수를 $f(x)$와 $g(x)$로 두고 적분을 진행한다. 이 때 $f(x)$와 $g(x)$로 두는 함수의 기준이 존재한다. 그 기준은 미분의 용이성과 적분의 용이성이다. 일명 로다삼지로 알려져 있는데 로그함수, 다항함수, 삼각함수, 지수함수를 뜻한다. 만약 로그함수에 가깝다면 미분이 쉬우므로 $f(x)$로, 지수함수에 가깝다면 적분이 쉬우므로 $g(x)$로 두어야 한다. 이는 추후 계산의 용이성을 위함이다. 두 함수를 두는 방법의 예로, 로그함수와 삼각함수가 곱해진 경우라면 로그함수는 $f(x)$로 삼각함수는 $g(x)$로 둔다. 또 다항함수와 지수함수가 곱해진 경우라면 다항함수를 $f(x)$로 지수함수를 $g(x)$로 둔다. 로다삼지의 예시로 로그함수는 $logx$, $\ln x$를 말하고, 다항함수는 $n$차 다항식/일차함수/이차함수를 말한다. 또 삼각함수는 $sin$, $cos$, $tan$, $secx$, $cscx$, $cotx$를 말하고, 지수함수는 $n^x$, $e^x$를 말한다. (참고로 지수함수를 부정적분하는 공식은 $\int e^{f(x)}dx = {e^{f(x)} \over f'(x)} + C$다.)

 

그렇다면 부분적분의 공식은 무엇이고 어떻게 유도될까? 부분적분의 공식은 다음과 같다.

 

$\int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx$

 

이를 유도하는 과정은 매우 간단하다. 부분적분은 미분가능한 두 함수 $f(x)$, $g(x)$가 있을 때 두 함수의 곱인 $f(x)g(x)$를 미분한다. 미분한 결과는 $\{f(x)g(x)\}' = f'(x)g(x) + f(x)g'(x)$이다. 이 상태에서 다시 적분하면 $f(x)g(x)$가 되어야 할 것이다. 따라서 양변을 x에 대해 적분하면 $f(x)g(x) = \int f'(x)g(x)dx + \int f(x)g'(x)dx$가 된다. 이 때$\int f'(x)g(x)dx$를 이항하게 되면 위 공식이 된다.

 

그렇다면 3개의 예시를 통해 실제로 부분적분을 적용해보자. 만약 $\int xe^xdx$라면 미분이 쉬운 다항식인 $x$를 $f(x)$로, 적분이 쉬운 지수함수인 $e^x$를 $g'(x)$로 둔다. 부분적분 공식에 의해 $\int xe^xdx = xe^x - \int 1\times e^xdx$가 되므로 결과적으로 $xe^x-e^x+C$가 된다. $e^x$를 적분하면 $e^x$가 되므로. (+미분해도 $e^x$)

 

두 번째로 $\int \ln xdx$라면 $f(x)$를 $\ln x$로 $g'(x)$를 1로 둔다. 부분적분 공식에 의해 $\int \ln xdx = x\ln x - \int {1\over x}xdx$이다. 따라서 $\int \ln x = x\ln x - \int dx$가 되므로 결과는 $\int \ln x = x\ln x - x + C$가 된다.

 

세 번째로 $\int x\sin 2xdx$라면 $f(x)=x$로, $g'(x)=\sin 2x$로 둔다. 부분적분 공식에 의해 $\int x\sin 2xdx = x\times -{1\over 2}cos2x - \int 1\times -1{1\over 2}cos2xdx$가 되고 추가 계산하면 결과적으로 $\int x\sin 2xdx = -{1\over 2}xcos2x + {1\over}4\sin 2x + C$가 된다.

 

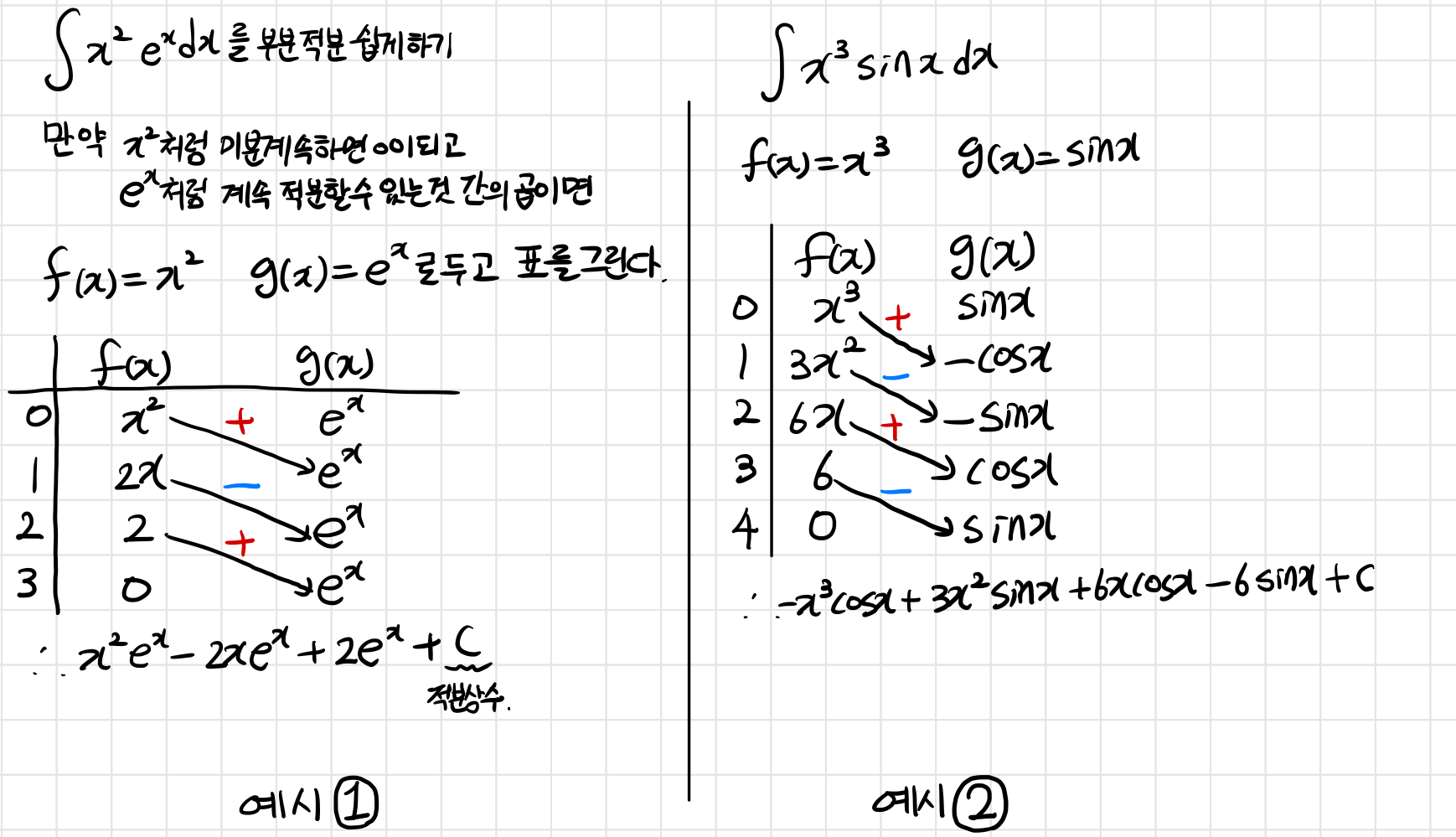
이러한 부분적분을 매우 쉽게할 수 있는 경우가 있다. 만약 계속 미분하면 0이되는 함수와 계속 적분할 수 있는 함수와의 곱이라면 가능하다. 아래 그림의 두 예시와 같은 과정으로 이뤄진다. 참고로 +와 -는 차례대로 번갈아가며 적용한다. 또 아래의 $g(x)$는 위의 $g'(x)$와 같다.

 

 

치환 적분

치환 적분은 복잡한 함성함수를 적분할 때 사용하는 방법으로 $ g(x) = t$ (이 때 g(x)는 미분가능 함수)와 같이 적분 변수($x$)를 다른 변수($t$)로 바꾸어 적분하는 방법이다. 예를 들어 $\int \cos(2x+1)dx$와 같은 함수를 적분해야 하는 상황에서 $2x+1 = t$와 같이 치환하여 단순화 시키는 것이다. 먼저 결론을 말하자면 치환 적분의 공식은 다음과 같다.

 

$\int f(x)dx = \int f(g(t))g'(t)dt$

 

그렇다면 이 치환 적분의 공식은 어떻게 유도될까? 간단하다. 먼저 $dy \over dx$는 $x$에 대한 $y$의 변화량이다. 하지만 이는 ${dy \over dx} = {dy \over dt} {dt \over dx}$로도 표현할 수 있다. 이후 $\int f(x)dx$라는 식이 있을 때 $x = g(t)$로 둔다. 이때 $x$를 미분하면 ${dx\over dt} = g'(t)$가 된다. 이를 기존의 식에 대입하면 $\int f(g(t))g'(t)dt$가 된다. 즉 $x$에 대한 적분을 $t$에 대한 적분으로 치환한 것이다.

 

이 치환 적분 공식을 2개의 예시에 적용해보자. 첫 번째로 $\int \cos (2x+1)dx$의 부정적분을 구해보자. 먼저 $2x+1 = t$로 둔다. 이후 양변을 $x$에 대해 미분하면 ${dt\over dx}=2$이므로, $dx={1\over 2}dt$가 된다. 따라서 이를 적분하고자 했던 식에 대입하면 $\int \cos t \times {1\over 2}dt$이 된다. 이제 이를 적분하면 ${1\over2} \sin t + C$의 형태가 되며 t에 대환 치환을 다시 $x$로 돌려주면 결과적으로 ${1\over 2}\sin (2x+1) +C$로 적분 계산 값이 도출된다.

 

두 번째 예시는 $\int x{\sqrt{x+1}}dx$이다. 마찬가지로 $x+1 = t$로 치환한다. $x$에 대해 미분하면 ${dt\over dx} = 1$이므로 $dt = dx$가 된다. 따라서 이를 대입해주면 $\int (t-1)\sqrt{t}dt$가 되고, 조금 난잡해보일 수 있지만 루트 표현식을 분수 표현식으로 바꾸면 $\int (t{3\over 2}-t{1\over 2})dt$가 된다. 이제 적분할 수 있다. 계산하면 ${2\over 5} t^2\sqrt{t} - {2\over 3}t\sqrt{t} +C$가 된다. $t$로 치환된 값을 다시 $x$로 풀어주면 결과적으로 ${2\over 5}(x+1)^2 \sqrt{x+1} - {2\over 3}(x+1)\sqrt{x+1} + C$로 적분 계산 값이 도출된다.

 

Reference

[1] 부분적분 쉽게하기 https://www.youtube.com/watch?v=E8N1E5ZAiIU 

[2] 부분적분, 치환적분 https://m.blog.naver.com/biomath2k/221860999596

[3] 치환적분 유도와 문제 예시 https://www.youtube.com/watch?v=SLnYC7mvyhk 

[4] 치환적분 문제 예시 https://blog.naver.com/biomath2k/221861047023