빈도주의(Frequentism)와 베이즈주의(Baysianism)
통계학에서 확률을 해석하는 두 관점이 있다. 그 관점은 빈도주의와 베이즈주의다. 빈도주의는 연역적 추론에 해당하며 베이즈주의는 귀납적 추론에 해당한다. 이러한 빈도주의와 베이주주의는 상호보완 관계에 있다. 빈도주의는 확률을 사건의 빈도로 보며, 반대로 베이즈주의는 확률을 사건 발생에 대한 믿음/척도로 바라본다. 또 빈도주의는 모수를 정적으로 전제되어 있는 상수로 보며, 반대로 베이즈주의는 모수를 동적이며 불확실한 변수로로 본다.
빈도주의는 사건을 여러 번 관측하여 발생한 확률을 검정하므로 사건이 독립성을 띤다는 장점이 있다. 예를 들어 동전 앞/뒷면을 여러 번 던져 관찰하게 되면 앞면도 0.5 뒷면도 0.5에 수렴하게 되며 앞면이 나올 확률이 0.5, 뒷면이 나올 확률이 0.5로 고정시킨다. 반면 베이지안주의는 동전이 앞면이 나왔다는 주장의 신뢰도가 50%다, 뒷면이 나왔다는 주장의 신뢰도가 50%라고 말한다. 빈도주의의 단점은 사건이 충분히 발생하지 못해 즉, 표본(데이터)이 부족할 경우 이러한 확률의 신뢰도가 떨어진다는 점이다.
베이즈주의는 이러한 빈도주의의 단점인 만약 여러 번의 사건을 관측할 수 없는 경우에 사용할 수 있다. 예를 들어 쓰나미의 예측 문제와 같다. 쓰나미가 발생하기 위해서는 여러 변수가 있다. 우선 지진이 발생해야하고 이로 인해 단층에 어긋남이 생기고 지형이 변화함에 따라 중력장이 발생할 때 주위로 퍼져나가면서 쓰나미가 된다. 이처럼 발생횟수가 적은 사건들에는 빈도주의를 적용할 수 없다. 다만 베이즈주의를 사용해 귀납적인 추론으로 쓰나미가 발생할 확률을 구할 수 있을 뿐이다. 본 글에서는 이러한 베이즈주의의 근간이 되는 베이즈 정리에 대해 정리하고자 한다.
베이즈 정리란?
베이즈 정리는 사전 확률(prior probability)과 사후 확률(posterior probability)의 관계를 나타내는 정리다. 이 베이즈 정리는 조건부 확률을 기반으로 한다. 조건부 확률이란 사건 $A$가 발생했다는 전제하에 사건 $B$가 일어날 확률이다. $P(B|A) = {P(B \cap A) \over P(A)}$로 표현한다. 베이즈 정리는 이 조건부 확률에서 유도된 것으로 다음과 같은 수식으로 나타낸다.
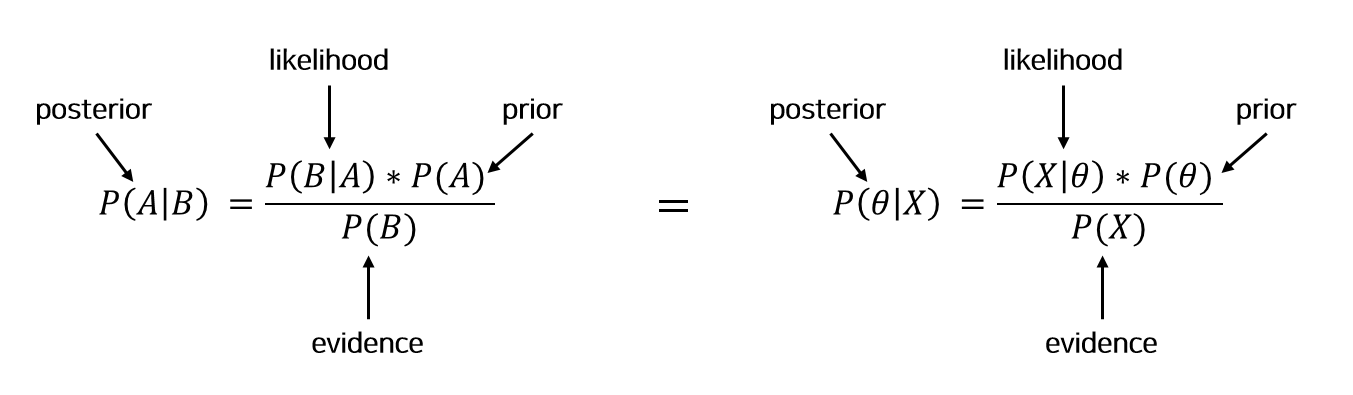
위 두 수식은 동일하게 베이즈 정리를 나타낸 것으로 변수명만 달리했다. 그 이유는 이해를 조금 더 쉽게 돕기 위함으로 왼쪽은 조건부 확률로부터 유도될 때 흔히 사용하고, 오른쪽은 베이즈 정리가 결국 모수($\theta$) 추정을 목적으로 한다는 것을 보이기 위함이다. 수식의 의미를 하나씩 분석해보자면, 먼저 posterior는 새로운 표본 X가 관측됐을 때 어떤 모수값을 갖는지를 의미한다. likelihood는 어떤 표본 X가 관찰되었을 때 어떤 확률분포를 갖는 모집단(모수)에서 추출되었을 확률을 의미한다. prior는 사전확률인 모수값을 의미하며, evidence는 모집단으로부터 표본 X가 관측될 확률이다. 결국 이 베이즈 정리를 요약하면 가능도(likelihood), 사전확률(prior), 관측 데이터(evidence)를 이용해 사후 확률(posterior)를 예측하는 방법이다.
베이즈 정리 유도
베이즈 정리를 유도하는 방법은 간단하다. 베이즈 정리 유도는 아래 식이 성립됨을 증명하는 것이다.
$P(A|B) = {P(A \cap B) \over P(B)} = {P(B|A)P(A) \over P(B)}$
증명을 위해 조건부 확률 두 개를 구해준 다음 분모를 이항하고 양변을 나눠주면 된다. 앞서 조건부 확률은 $P(A|B) = {P(A\cap B) \over P(B)}$라고 했다. 이를 반대로 하면 $P(B|A) = {P(B\cap A) \over P(A)}$이다. 여기서 양변에 분모를 곱해주면 다음과 같은 형태가 된다.
$P(A|B)P(B) = P(A\cap B)$
$P(B|A)P(A) = P(B\cap A)$
이 때, $P(A\cap B) = P(B\cap A)$이므로
$P(A|B)P(B) = P(B|A)P(A)$가 되고 여기서 양변을 $P(B)$로 나눠주면
$P(A|B) = {P(B|A)P(A) \over P(B)}$가 된다.
베이즈 정리 예시: 스팸 메일 확률 예측
스팸 메일 필터는 특정 단어 포함 여부를 기준으로 스팸 여부를 판단한다. 어떤 한 회사에 수신되는 메일 중 30%가 스팸메일이고 70%가 정상메일이다. 또 스팸메일 내용엔 A란 특정 단어가 포함될 확률이 40%고 정상 메일은 10%다. 이 때 A라는 단어가 보일 때 이 메일이 스팸메일일 확률은 얼마인가?
$P(S) = 0.3$ (스팸메일일 확률)
$P(N) = 0.7$ (정상메일일 확률)
$P(A|S) = 0.4$ (스팸메일에 A가 포함될 확률)
$P(A|N) = 0.1$ (정상메일에 A가 포함될 확률)
$P(A) = 0.19$ (A가 정상메일/스팸메일 모두 포함될 확률)
$P(A)$의 경우 스팸메일에 A가 포함될 확률 + 정상메일에 A가 포함될 확률이다. 두 사건은 상호배타적이므로 덧셈법칙을 사용해 계산할 수 있다. 즉 $P(A) = (P(A|S) * P(S)) + (P(A|N) * P(N))$이다. 이를 계산하면 $(0.4 * 0.3) + (0.1 * 0.7) = 0.19$이다. 즉 $P(A) = 0.19$다.
이렇게 사전 정보를 전부 구했으니 A라는 단어가 보일 때 스팸메일일 확률인 $P(A|S)$를 구해보자. $P(A|S) = {P(A\cap S) \over P(S)}$다. 여기서 이항해주면 $P(A|S)P(S) = P(A\cap S)$다. 이를 계산하면 $0.3 \times 0.4 = 0.12$다.
$P(S|A) = {P(S\cap A) \over P(A)} = {0.12 \over 0.19} = 0.6315$
즉 사전 확률인, A라는 단어가 보일 때 해당 메일이 스팸메일일 확률이 0.6315가 된다.
Reference
[1] https://ko.wikipedia.org/wiki/베이즈_추론
[2] https://brunch.co.kr/@aischool/3
'Artificial Intelligence > 확률-통계학' 카테고리의 다른 글
| [확률/통계] 적률추정법 이해하기 (Method of Moments Estimator) (0) | 2022.10.23 |
|---|---|
| [확률/통계] 가설 검정 이해하기 (귀무가설, 대립가설) (0) | 2022.10.21 |
| [확률/통계] 누적분포함수 (CDF, Cumulative Distribution Function) (0) | 2022.10.10 |
| [확률/통계] 확률분포 총 정리 (이산확률분포, 연속확률분포) (0) | 2022.09.29 |
| [확률/통계] 모수 추정과 추정량, 추정치 (1) | 2022.09.28 |