가설 검정이란?
가설 검정이란 어떤 추측이나 가설에 대해 타당성을 조사하는 것이다. 통계학에서 가설 검정은 표본통계량으로 모수를 추정할 때 추정한 모수값 또는 확률 분포 등이 얼마나 타당한지 평가하는 통계적 추론이다. 이 가설 검정에는 크게 귀무가설과 대립가설이 쓰인다. 귀무가설(null hypothesis)은 처음부터 버릴 것으로 예상하는 가설이며, 대립 가설(alternative hypothesis)은 귀무가설과 반대로 실제로 주장하거나 증명하고 싶은 가설이다.
가설 검정 단계는?
귀무가설과 대립가설을 통해 가설 검정을 진행하는 단계는 크게 4단계로 이루어진다.

위 4단계의 과정을 제약회사의 신약 개발 예시를 들어 설명하면 다음과 같다.
1. 귀무가설과 대립가설을 수립한다.
귀무가설($H0$): 신약이 효과가 없을 것이다. 따라서 제약회사에 유의미한 수익 창출이 어려울 것이다.
대립가설($H1$): 신약이 효과가 있을 것이다. 따라서 제약회사에 유의미한 수익 창출이 가능할 것이다.
이 때 귀무 가설은 보통 $H0$로 표현하며 대립 가설은 $H1$로 표현한다. 두 가설들은 아래 단계들을 거쳐 하나가 채택된다.
2. 유의수준(significant level, $\alpha$)을 설정한다.
유의수준은 가설 예측을 100% 옳게 할 수 없으므로 오차를 고려하기 위한 것이다. 유의수준을 통해 귀무가설 채택여부 결정한다. 일반적으로 $\alpha = 0.05$로 설정하지만 검정 실시자의 결정에 따라 달라질 수 있다. 여기서 만약 $\alpha=0.05$로 설정한다면 이 값을 기준으로 귀무가설 또는 대립가설을 채택한다. 만약 이후 단계들로부터 검정 통계량을 기반으로 하는 p-value가 산출되었을 때 0.05보다 낮다면 귀무가설을 기각하고 대립가설을 채택한다.
유의수준을 정할 때 함께 결정해야 하는 것은 양측 검정/단측 검정이다. 양측검정은 두 가설 모두에 관심 있을 때 사용하며 단측검정은 한 가설에만 관심 있을 때 사용한다. 예를 들어 제약회사 예시에서는 신약 효과가 있는지만 증명하면 자연스럽게 효과가 없음도 증명할 수 있으므로 단측 검정을 사용할 수 있다. 하지만 만약 남자와 여자의 스트레스의 차이를 두고 가설이 수립되었다면 양쪽 모두 살펴보아야 하므로 양측 검정을 사용해야 한다.
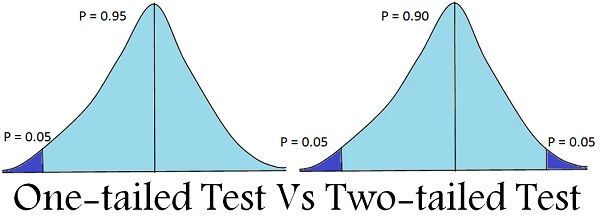
(* 유의수준과 함께 사용되는 기각역이라는 것은 단측 검정과 양측 검정에 위치하는 유의수준 $\alpha$ 크기에 해당하는 영역을 의미한다.)
3. 검정 통계량을 계산후 p-value를 도출한다.
검정 통계량은 모수 추정을 위해 구하는 표본 통계량과 같은 의미를 가지는 것으로 가설 검정시 사용하는 표본 통계량을 뜻한다. 또 검정 통계량은 표본을 통해 가설 검정에 사용하는 확률 변수이다. 확률 변수라는 것은 그래프 상에서 x축을 나타내는 것이므로 확률 변수에 대한 확률 값을 나타내는 y값과는 다르다. 따라서 이 검정 통계량(확률 변수)은 확률분포 상에서 x축을 의미한다. 이 검정 통계량을 구하기 위해 사용하는 방법들은 아래와 같이 Z검정, T검정, 카이제곱 검정, F검정 등이 있다.
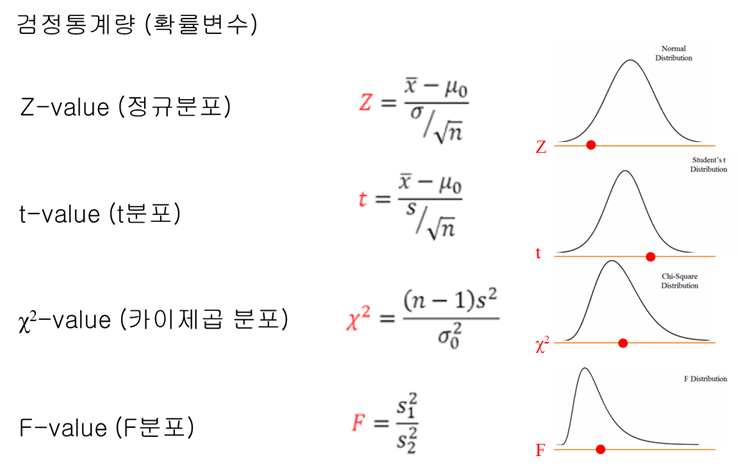
이쯤에서 혼동되는 것은 검정이라 부르는것과 분포라 부르는 것은 어떤 차이를 가질까? 핵심은 내부적으로 사용하는 함수 식이 다르다. 예를 들어 검정에서 사용되는 함수는 검정력 함수라 부르는 것으로 확률분포의 x축 값을 검정력 함수에 넣어 검정 통계량을 구하는데 사용한다. 반면 분포는 x축과 함께 y축은 확률을 구해 확률분포로 나타낼 수 있는 식이다. 위의 그림에선 검정력 함수만 나타내고 있다.
이제 가설 검정의 핵심인 p-value(유의 확률)을 구하기 위해서는 위 검정력 함수를 통해 구한 검정 통계량을 알아야 한다. 예를 들어 아래와 같이 Z분포를 따르는 검정통계량이 있고 Z검정을 통해 어떤 한 표본의 검정통계량 z를 구했을 때 x축 위의 z지점까지의 누적분포함수가 곧 p-value가 된다.
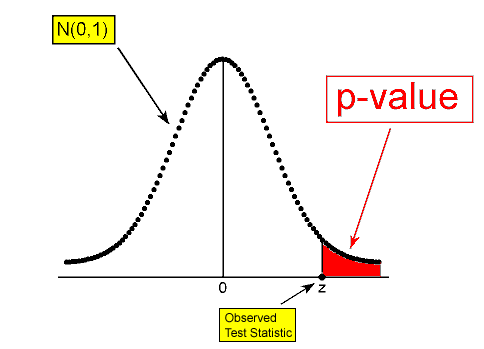
4. p-value를 기준으로 귀무가설 채택 여부를 결정한다.
만약 위 그래프에서 검정 통계량 z가 기각역이라 불리는 유의수준 $\alpha$ 영역 내에 위치하게 된다면 귀무가설을 기각하고 대립가설을 채택하게 된다. 즉 p-value가 유의수준 $\alpha$보다 같거나 작다면 귀무가설을 기각하고, p-value가 유의수준 $\alpha$보다 크다면 귀무가설을 채택한다.
제약회사 예시에서 만약 신약 효과가 없을 확률이 유의수준($\alpha=0.05$)보다 작다면 효과가 없다는 귀무가설을 기각하고 효과가 있다는 대립가설을 채택하는 것이다. 반대로 만약 신약 효과가 없을 확률이 유의수준($\alpha=0.05$)보다 크다면 신약 효과가 없을 확률이 더 높은 것이므로 귀무가설을 채택하고 대립가설을 기각한다.
1종 오류와 2종 오류
1종 오류
쉽게 말해 1종 오류란 귀무가설이 참인데 기각한 경우를 말한다. 예를 들어 신약이 효과가 있어 제약회사에서 많은 수익을 벌었지만 알고보니 신약이 효과가 없었을 때를 의미한다. 즉 귀무가설을 기각하고 대립가설을 채택했지만 이것이 잘못된 검정이었음을 뜻한다. 이에 의거하면 p-value의 의미는 1종 오류를 얼마나 범할 확률을 나타내기도 한다. 즉 p-value가 5%라면 100번 검정하면 5번 정도 1종 오류가 발생하는 것이다. 또 이에 따라 유의 수준 $\alpha$는 1종 오류의 상한선이라고 말할 수 있다. 따라서 검정 결과 p-value가 $\alpha$보다 낮다면 상한선을 벗어나지 않으므로 이를 귀무가설을 기각하고 p-value가 $\alpha$보다 높다면 상한선을 벗어났으므로 귀무가설을 채택한다.
2종 오류
쉽게 말해 2종 오류란 귀무가설이 거짓인데 참으로 판단한 경우를 의미한다. 예를 들어 신약이 효과가 없다는 귀무가설이 사실로 밝혀져서 제약회사에서 생산과 판매를 그만두었지만 알고보니 효과가 있었을 때를 의미한다.
Reference
[1] [개념 통계 21] 가설 검정 방법과 원리 - 필로홍
[4] Difference Between One-tailed and Two-tailed Test
'Artificial Intelligence > 확률-통계학' 카테고리의 다른 글
| [확률/통계] 모수적 방법과 비모수적 방법 (parametric and non parametric) (0) | 2022.10.23 |
|---|---|
| [확률/통계] 적률추정법 이해하기 (Method of Moments Estimator) (0) | 2022.10.23 |
| [확률/통계] 베이즈 정리 이해하기 (Bayesian Theorem) (0) | 2022.10.11 |
| [확률/통계] 누적분포함수 (CDF, Cumulative Distribution Function) (0) | 2022.10.10 |
| [확률/통계] 확률분포 총 정리 (이산확률분포, 연속확률분포) (0) | 2022.09.29 |