누적분포함수란 확률론에서 주어진 확률분포가 특정 값보다 작거나 같은 확률을 나타내는 함수이다. 이 특정 값이라는 것은 어떤 사건을 의미하므로 누적분포함수는 어떤 사건이 얼마나 많이/적게 나타나는지에 관한 함수라고도 할 수 있다. 누적분포함수의 대표적인 특징은 확률변수가 이산형/연속형과 무관하게 모든 실수값을 출력한다는 것이다. 예를 들어 주사위를 던져 특정 값이 나올 확률변수 X의 값이 아래와 같이 1~6로 주어져 있다고 가정하자.
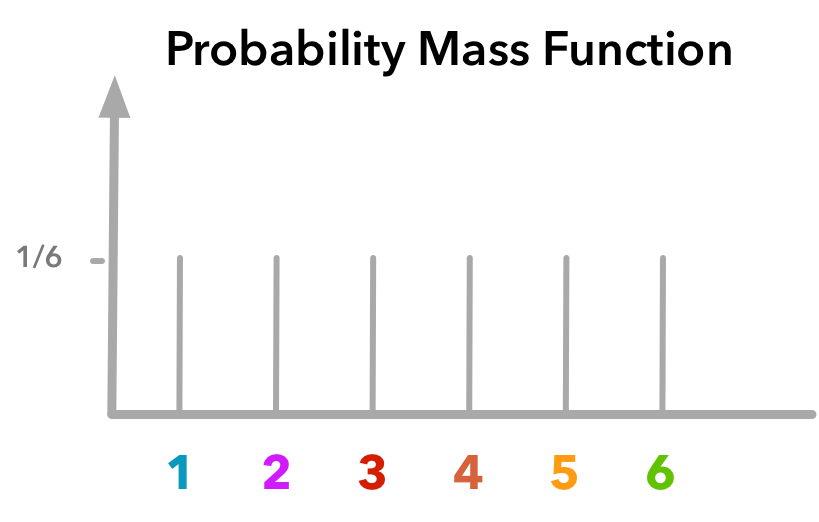
이 때 만약 확률변수 X가 2보다 같거나 낮은 수가 나타날 확률이 얼마일까? 고민할 것 없이 1, 2 두 가지 경우이므로 $2\over 6$이다. 그렇다면 만약 확률변수 X가 2.5보다 작거나 같은 경우와 같이 X가 실수 값을 가지는 경우는 어떻게 해야할까? 이 또한 마찬가지다. 확률변수는 이산 값만 갖고 있으므로 2.5보다 같거나 낮은 경우는 1, 2를 가질 경우이니 $2\over 6$다. 또 만약 확률변수 X가 10보다 작거나 같을 확률을 묻는다면? 1, 2, 3, 4, 5, 6 모든 경우가 해당하므로 ${6\over 6} = 1$이 된다. 이처럼 누적분포함수는 확률변수가 이산확률변수/연속확률변수와 무관하게 실수값을 입력으로 받을 수 있다. 이러한 누적분포함수를 수식으로는 다음과 같이 나타낸다.
$F(a) = P(X \leq a) = \sum_{x \leq a} p(x)$
수식을 세 부분으로 나누어 분석해보자면 왼쪽에 가까울수록 추상성을, 오른쪽으로 갈수록 구체성을 띤다. 가장 맨 왼쪽의 함수 $F$는 누적분포함수를 의미한다. 누적분포함수는 특정확률변수보다 같거나 작을 확률을 표현하는 함수이므로 특정확률변수로 $a$를 입력으로 한다. 가운데 식도 마찬가지다 어떤 사건에서 발생할 수 있는 여러 확률변수 중에서 $a$보다 작은 확률변수들의 확률값을 구하는 것이다. 오른쪽 식도 동일하다. $a$보다 작은 확률변수 x에 대해서 모든 합을 구해주는 것이다. 위 주사위 예를 들어 2.5보다 작을 확률이면 $a=2.5$가 되고 확률변수 x는 1,2를 가질 수 있으므로 위 식의 값은 $2\over 6$이 된다. 이러한 누적분포를 그래프로는 다음과 같이 표현할 수 있다.

위 그림에서 확인할 수 있듯 누적분포함수(CDF)는 확률밀도함수(PDF) 전체에 대한 부분을 표현하는 함수라고도 할 수 있다. PDF가 확률변수가 가질 수 있는 전체 확률 분포를 표현한 것이라면, CDF는 전체 확률 분포에서 확률변수가 $a$ 보다 작을 확률이다. 위 예시에서는 $a=1$보다 작을 확률이 되겠다. 이러한 확률밀도함수와 누적분포함수와의 관계를 다르게 말해서, 확률밀도함수를 적분하면 누적분포함수가 되며 또 반대로 누적분포함수를 미분하면 확률분포함수가 된다고 표현할 수 있다.
Reference
[1] https://www.youtube.com/watch?v=vMBxOtGhFQ0
[2] https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jung1pp&logNo=221597577634
'Artificial Intelligence > 확률-통계학' 카테고리의 다른 글
| [확률/통계] 적률추정법 이해하기 (Method of Moments Estimator) (0) | 2022.10.23 |
|---|---|
| [확률/통계] 가설 검정 이해하기 (귀무가설, 대립가설) (0) | 2022.10.21 |
| [확률/통계] 베이즈 정리 이해하기 (Bayesian Theorem) (0) | 2022.10.11 |
| [확률/통계] 확률분포 총 정리 (이산확률분포, 연속확률분포) (1) | 2022.09.29 |
| [확률/통계] 모수 추정과 추정량, 추정치 (1) | 2022.09.28 |