For a better world

멱급수 (Power Series)

멱급수 이전에, 먼저 급수란 규칙이 있는 수열의 합을 의미한다.

예컨데 등차수열의 합이나 등비수열의 합도 급수이다. 등비수열의 합을 나타내는 식은 아래와 같은데, 

$S_n = a + ar + ar^2 + ar^3 + \dots + ar^{n-1}$

위와 같은 일반적인 급수는 각 항에 단순한 숫자가 들어가는 것이 특징이다. 하지만 멱급수의 경우 같은 형태를 띠지만 숫자가 아닌 $x$와 같은 문자로 표현되는 것이 특징이다. 가령 수식으로 나타내면 아래와 같다.

$f(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + \dots = \sum_{n=0}^\infty a_nx^n$

이러한 멱급수는 언제 사용될까? 멱급수는 물리학이나 수학에서 처음부터 정확한 해를 찾기 어려울 때 근사치를 통해 점점 근사한 값을 찾아갈 때 사용한다. 즉, 찾고자 하는 함수나 해가 어떤 형태나 값인지 잘 모를 경우 멱급수로 가정하고 문제를 풀게 되면 근사 함수나 근사 해를 구할 수 있는 것이 특징이다. 이 때 정확한 함수나 정확한 해를 구할 수 없는 것은 실사용의 편의를 위해 고차원이 되는 항은 제외하고 2차항 또는 3, 4차항만 구한 뒤, 이를 구하고자 했던 함수 또는 해라고 판단한다. 실제로 멱급수는 양자역학에서 원자핵 주위를 도는 전자와 같이 미시세계를 다룰 때 2차항 정도까지만 고려해도 계산값과 측정값이 근사하기 때문에 유용하게 쓰인다고 한다. 

테일러 급수 (Taylor Series)

테일러 급수란 여러 번 미분가능한 함수 $f(x)$에 대해 $x=a$에서 그 $f(x)$에 접하는 멱급수로 표현하는 방법이다. 테일러 급수를 사용하는 방법은 무한개의 항을 가진 멱급수를 통해 어떤 함수를 표현하는 것이다. 하지만 실 사용에서는 편의를 위해 몇 개의 항만 사용해 근사의 형태로 활용한다.

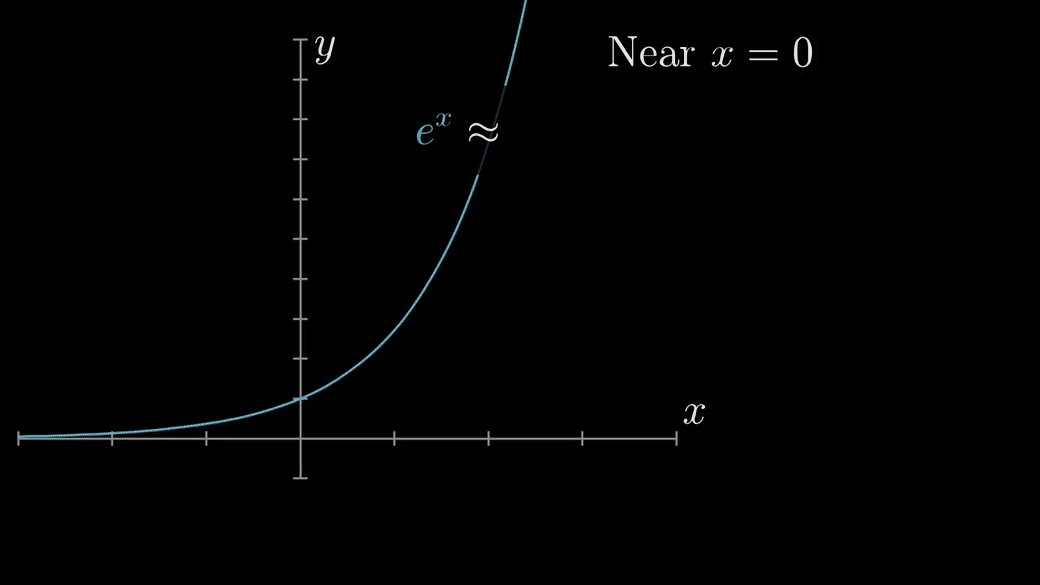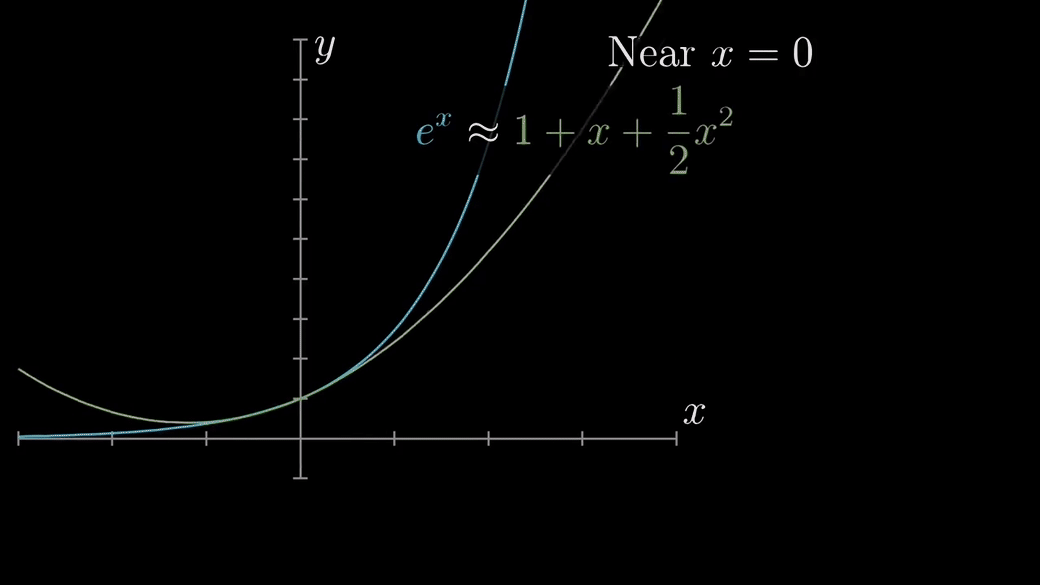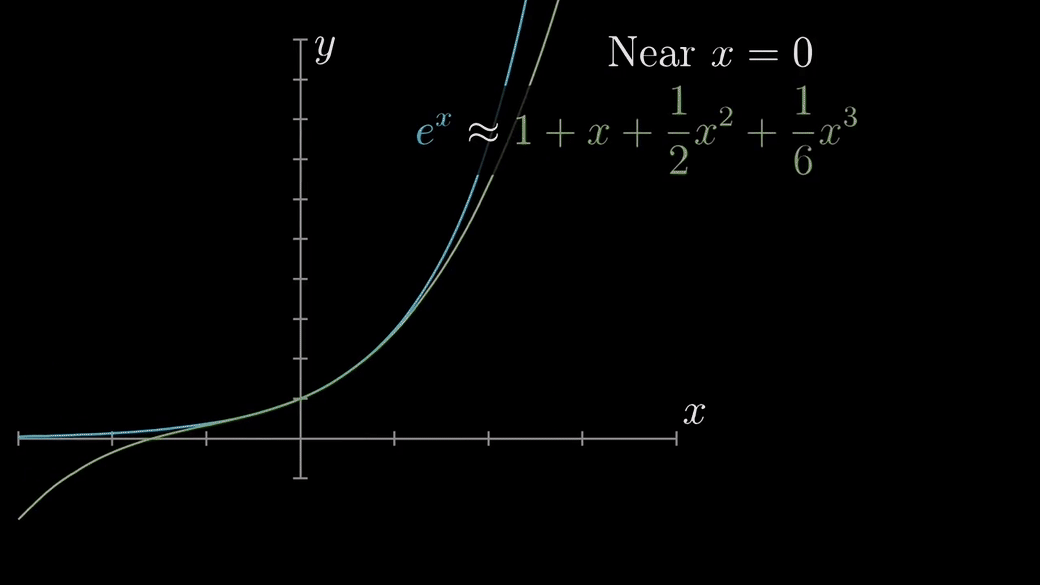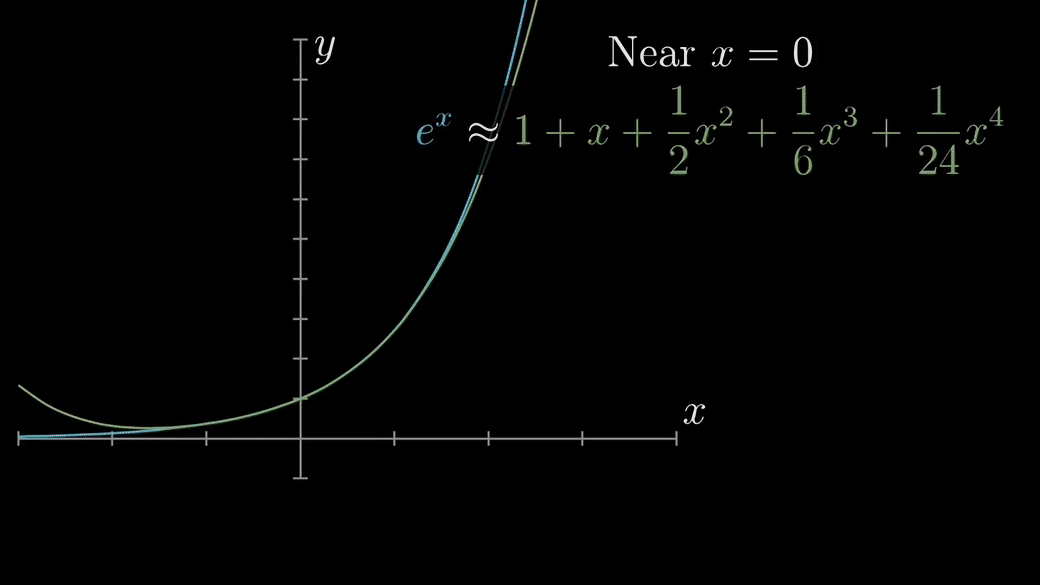
일반화한 수식으로 나타내면 다음과 같다.

$f(x) = \sum_{n=0}^\infty {f^{(n)}(a) \over n!} {(x-a)}^n$

테일러 급수의 특징은 $x$가 $a$ 근처에서만 성립하는 것이다. 만약 $x$가 $a$로부터 멀어지면 멀어질수록 큰 오차를 갖게 된다. 또한 테일러 급수를 활용해서 무한히 미분가능한 f(x)를 우리가 찾고자 하는 함수에 무한히 근사한다고 해도 같아지지 않을 수 있다. 예컨데 아래와 같이 항의 개수(N)가 많아질수록 오히려 근사 함수에 수렴하는 것이 아니라 어느 특정 구간에서 오차가 크게 생기는 것을 확인할 수 있다.

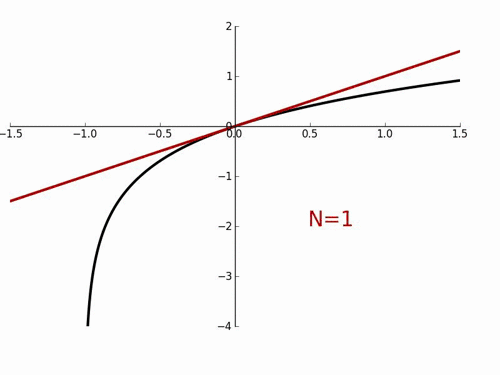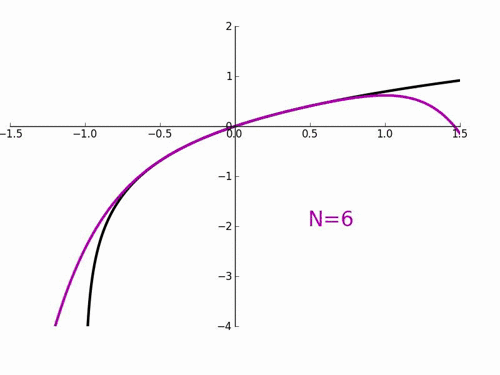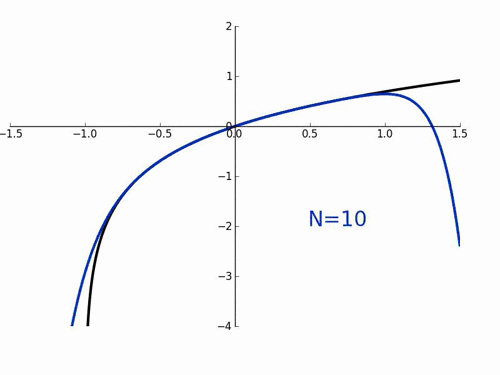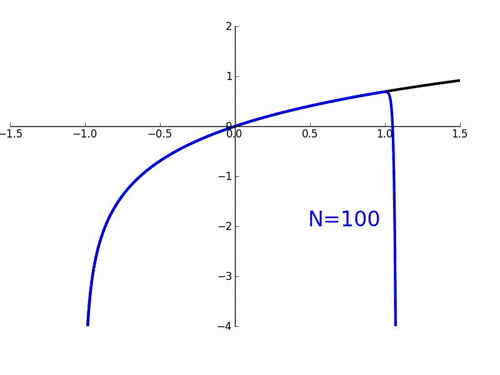
우리는 찾고자 하는 함수에 근사하기 위해서는 테일러 급수 f(x)에서 $x=a$인 $f(a)$가 필요하다. 

(1) $f(x) = a_0 + a_1(x-a) + a_2(x-a)^2 + a_3(x-a)^3 + a_4(x-a)^4 + \dots$

의 수식이 있을 때 (0)과 같이 일반화한 수식으로 나타내기 위해서는 미분한 식에 $x=a$를 대입하면 된다. 과정은 아래와 같다.

(1)의 식을 한 번 미분하게 되면 아래와 같은 함수를 얻을 수 있다. 

$f'(x) = a_1 + 2a_2(x-a) + 3a_3(x-a)^2 + 4a_4(x-a)^3 + \dots$

위의 식에 $x=a$를 대입하게 되면 모두 사라지고 하나의 항만 남아 $f'(a) = a_1$이 된다.

(1)의 식에 두 번 미분하게 되면 아래의 식이 된다

$f''(x) = 2a_2 + 2 * 3a(x-a) + 3*4a_4(x-a)^2+\dots$

위의 식에 $x=a$를 대입하게 되면 모두 사라지고 하나의 항만 남아 $f''(a) = 2a_2$이 된다. 즉, $a_2 = {1\over2} f''(a)$이다

(1)의 식에 세 번 미분하게 되면 아래의 식이 된다.

$f'''(x) = 2 * 3a_3 + 2*3*4a_4(x-a)+\dots$

위의 식에 $x=a$를 대입하게 되면 모두 사라지고 하나의 항만 남아 $f'''(a) = 2*3a_3$이 된다. 즉, $a_3 = {1\over{2*3}} f'''(a)$이다.

위와 같은 절차를 정리해서 테일러 급수를 표현하면 아래와 같다.

$f(x) = f(a) + {1\over 1!}f'_{(a)}(x-a) + {1\over 2!}f''_{(a)}(x-a)^2 + {1\over 3!}f'''_{(a)}(x-a)^3 + \dots + {1\over n!}f^n_{(a)}(x-a)^n$

결론을 정리하면 어떤 함수에 근사하는 함수를 찾기 위해 어떤 함수를 테일러 급수의 형태로 나타낸 다음, 미분을 통해서 찾고자 하는 함수에 점점 근사해 나갈 때 사용된다. 

매클로린 급수 (Maclaurin's Series)

매클로린 급수는 테일러 급수에 포함되는 개념이라 볼 수 있다. 테일러 급수의 특정한 경우에 사용되는 급수이다. 매클로린 급수는 $a=0$일 때를 의미하는 원점 근처에서 함수를 급수 전개 한것을 의미한다. 테일러 급수에서 사용되는 $x-a$를 $x$로만 바꾸면 되기에 더 간단한 형태이다. 

$f(x) = \sum_{n=0}^\infty {f^{(n)} \over n!} {x}^n$

Reference

[1] http://www.aistudy.com/math/optimization.htm

[2] https://nacture.kr/70

[3] https://crush-on-study.tistory.com/93