For a better world

데이터 사이언스 직군으로 면접보며 받았던 질문에 대해 정리 (Last Update: 2022.11.29)

1. Deep Learning

Q1. ReLU의 단점을 설명하라.

ReLU의 경우 Sigmoid의 단점인 gradient vanishing 문제를 극복하기 위해 사용한 활성화 함수입니다.  ReLU의 장점은 입력값을 그대로 출력하기 때문에 구현이 쉽고 빠른 학습이 가능합니다. 반면 단점은 Dead ReLU 현상으로 만약 입력값이 음의 값이 들어온다면 이를 처리하지 못하는 것입니다. 이와 같이 음의 값을 처리하지 못하는 단점을 보완하기 위해 LeakyReLU와 같은 활성화함수를 사용합니다.

Q2. 모델의 일반화 성능을 위해 사용할 수 있는 방법을 설명하라.

모델 일반화 성능 향상을 위해 크게 3가지 관점으로 접근할 수 있습니다. 첫 번째는 데이터 관점, 두 번째는 모델 관점, 세 번째는 하이퍼파라미터 관점입니다. 첫 번째 데이터 관점에서는 학습 데이터셋을 추가하거나 어그멘테이션을 통해 모델 성능을 향상시킬 수 있습니다. 또 학습 데이터셋에 전처리를 통해 더미값과 같은 데이터를 제거해줌으로써 모델 성능을 향상시킬 수 있습니다. 두 번째 모델 관점에서는 트랜스포머 모델을 사용해 RNN 계열 모델의 단점인 long-term dependency와 비병렬성을 극복한 것처럼 더 좋은 모델 아키텍처를 사용하는 방법이 있습니다. 이를 위해 NAS(Neural Architecture Search)와 같은 알고리즘을 사용할 수 있습니다. 또 모델에 오버피팅을 줄이기 위해 BREDLAN이라고하여 Batch Normalization, Regularization, Early Stopping, Dropout, Label Smoothing, Augmentation, Noise Robustness를 적용할 수 있습니다. 마지막 하이퍼파라미터 관점에서는 Random Search나 Grid Search, HyperBand, Keras Tuner등을 통해 손실함수, 학습률, 활성화함수, Optimizer 등의 하이퍼파라미터의 최적값을 찾음으로써 모델의 성능을 향상시키고 일반화할 수 있습니다.

Q3. Word2vec 모델에 대해 설명하라.

word2vec 모델은 2013년에 나온 모델로 기존의 NNLM(Neural Network Language Model)의 단점을 보완하고자 나온 모델이라 할 수 있습니다. 기존 NNLM 모델은 단어를 벡터화시키기 위해 discrete한 방식인 one-hot encoding 방식을 사용했습니다. 하지만 이 방식은 sparse-matrix가 만들어지기 때문에 고차원 상에서 비효율적으로 분산 표상되어 학습이 잘 이루어지지 않습니다. 때문에 이를 continous하게 표상할 수 있도록 만들어진 모델이 word2vec 입니다. word2vec은 내부적으로 학습방식이 CBOW와 Skip-gram으로 나뉩니다. CBOW는 주변단어인 context에 기반해 중심단어를 예측하는 방식이며 Skip-gram은 중심단어에 기반해 주변단어를 예측하는 방식입니다. 두 방식 모두 Input layer, projection layer, output layer 3가지 레이어로 구성되어 동작합니다. 

Q4. CNN의 장점과 단점을 설명하라.

CNN의 장점은 DNN의 단점을 극복한 것입니다. DNN을 통해 3차원인 이미지를 학습한다면 많은 수의 파라미터가 필요하고 오버피팅이 일어나기 쉽습니다. 반면 CNN을 사용하면 DNN에 비해 파라미터 수를 감소시켜 학습이 가능합니다. 또 DNN과 달리 CNN은 이미지의 공간적 형태를 보존합니다. DNN은 이미지의 픽셀간 관계를 고려하지 않고 1차원으로 flatten시키지만 CNN은 픽셀간 관계를 고려할 수 있습니다. CNN의 단점은 풀링 과정에서 정보손실이 발생하는 것입니다. 풀링 과정을 거치면서 정보가 요약됩니다. 이 때 각각의 local feature의 상대적인 위치 정보를 잃을 수 있습니다.

Q4-1 CNN의 동작원리를 설명해라. (예상)

우선 CNN의 구조는 convolution layer와 pooling layer, fully-conncected layer로 구성됩니다. convolution layer를 통해 Input image로부터 feature map을 추출합니다. 추출 과정은 input image에 filter로 슬라이딩 윈도우를 통해 합성곱을 계산하는 방식으로 이루어집니다. 이후 pooling layer를 통해 feature map의 크기를 줄이고 feature를 추출합니다. 최종적으로 flatten 시킨 다음 fully-connected layer에 입력하여 최종 결과를 출력하는 방식으로 동작합니다. 

Q5. RNN의 장점과 단점을 설명하라.

RNN은 시퀀셜 데이터를 처리하기 위해 사용하는 신경망의 한 종류입니다. RNN의 장점은 정의 자체로서 시퀀셜 데이터를 처리할 수 있다는 데 있습니다. 반면 단점은 long-term dependency 문제가 있고 RNN 구조상 병렬처리가 불가능합니다. 이러한 RNN 계열의 단점을 극복하기 위해 Transformer가 고안되었습니다. Transformer는 attention 메커니즘을 사용해 RNN 계열의 단점인 long-term dependency 문제와 비병렬성 문제를 해결했습니다.

Q5-1. RNN의 동작원리를 설명해라. (예상)

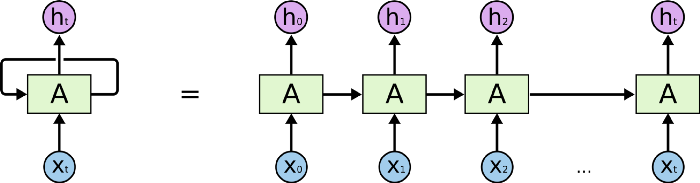
RNN은 크게 Input layer, hidden layer, output layer로 구성되어 있습니다. RNN의 가장 큰 특징은 은닉층이 이전 데이터를 참조하도록 연결되어 있다는 것입니다. 즉 만약 t시점에서 입력 데이터가 들어왔다면 t시점에서 출력하는 것 뿐만 아니라 t+1 시점의 출력에도 영향을 미칩니다. 따라서 시퀀셜한 데이터 처리에 적합하다는 장점이 있습니다. 반면 단점은 long-term dependency 문제가 발생합니다. 가령 오래된 시점에서 입력된 데이터의 영향이 뒤로 갈수록 적어지는 것을 의미합니다. 이러한 문제점을 해결하기 위해서는 LSTM에서 cell state란 개념을 도입해 이를 해결했습니다. 

Q5-2. long-term dependency 문제가 발생하는 이유는 무엇인가요?

핵심은 기울기 폭발과 기울기 소실 문제 때문입니다. RNN은 활성화함수로 tanh를 사용합니다. tanh는 -1과 1사이의 값을 가집니다. 이 때 1보다 작은 값이 반복해서 곱해지기 때문에 feed-forward 관점에선 앞의 정보를 충분한 세기로 전달할 수 없고 back-propagation 관점에서는 tanh 함수의 기울기가 0에 가깝거나 큰 값이 발생할 수 있어 기울기 폭발과 소실 문제가 발생합니다. 참고로 이 때문에 LSTM에서는 기존 RNN 구조에 cell state라는 변수를 추가함으로써 long-term dependency 문제를 해결합니다.

Q5-3. LSTM의 동작원리를 설명해라. (예상)

LSTM은 RNN 계열 모델로 RNN의 단점인 long-term dependency 문제를 해결하기 위해 만들어졌습니다. 이 장기의존성 문제를 해결하기 위핸 핵심 개념은 cell-state입니다. LSTM의 구조는 RNN과 유사하지만 내부적으로 게이트가 3개 있습니다. forget gate, input gate, output gate입니다. forget gate에서는 이전의 hidden state와 현재 시점의 Input을 받아 sigmoid 함수를 거쳐 0과 1사이의 값으로 출력합니다. 1이 출력되면 위 cell state의 값과 점곱을 통해 그대로 보내주고 0이 출력되면 cell state의 값이 0으로 초기화 됩니다. 만약 0~1 사이 값이 나오면 일부 정보는 지워진 채 cell state에 업데이트 됩니다. 이후 두 번째 Input gate에서는 sigmoid 함수와 tanh 함수가 있습니다. sigmoid 함수를 거쳐 나온 값과 tanh를 거쳐 나온 값을 점곱을 통해 cell state에 업데이트 해줍니다. 마지막으로 output gate에서는 hidden state 값과 현재 시점의 input값을 마찬가지로 sigmoid 함수를 거친 뒤 tanh함수와 점곱되어 출력됩니다. 그러면 최종적으로 다음 레이어로 넘어갈 cell state가 완성되는 형태입니다. 이러한 LSTM 구조를 사용할 경우 기존의 RNN에서 발생하는 long-term dependency 문제를 해결할 수 있습니다.

Q6. 트랜스포머 구조에 대해 설명하라.

트랜스포머 구조는 크게 인코더와 디코더로 구성이 되어 있습니다. 소스 시퀀스를 인코더에 넣고 압축한 다음 디코더를 통해 타겟 시퀀스를 생성하는 방식으로 동작합니다. 인코더에는 크게 3가지로 MultiHeadAttention 레이어, Poisitionwise FeedForward 레이어, skip connection이 포함된 Layer Normalization 레이어로 구성되어 있습니다. 반면 디코더도 동일하지만 추가적으로 Masked MultiHeadAttention 레이어가 포함되어 있습니다. 트랜스포머의 핵심은 self-attention 메커니즘을 사용한 Query, Key, Value 행렬의 Interaction이라 할 수 있습니다. $Softmax({QK^T \over \sqrt{d_K}})V$로 표현하며 동작 방식은 Query 행렬과 Key 행렬의 전치행렬을 곱해준 다음 smoothing을 위해 $\sqrt{d_K}$ 차원으로 나눠줍니다. 이후 softmax 함수를 취해준 다음 Value 행렬을 곱해주는 방식입니다.

Q7. Adam Optimizer 동작을 설명하라.

먼저 학습은 모델의 예측값과 정답값 사이의 오차를 최소화하는 방향인 Gradient를 구하고 이 방향에 맞춰 모델 전체 파라미터를 업데이트 하는 과정입니다. 이 오차를 최소화 하는 과정을 최적화라고하며 Optimizer는 이 최적화를 위해 사용합니다. 종류는 Stochastic Gradient Descent부터, Momentum, AdaGrad, RMSProp, AdaDelta, Adam, NAdam, Radam, AdamW, AdamP 등이 있습니다. 여기서 Adam이란 Adaptive Moment Estimation을 의미하는 것으로 수리통계학의 적률(모멘트)이란 개념에 기반합니다. (추가 작성 예정)

Adam은 RMSProp과 Momentum 방식을 합쳐 만든 알고리즘입니다. 기울기값의 지수평균과 기울기 제곱값의 지수평균을 활용해 step size를 조절합니다. Adam은 RMSProp과 Momentum 방식을 합쳐 만든 알고리즘입니다. RMSProp와 마찬가지로 기울기 제곱값의 지수 평균을 저장하고, Momentum과 마찬가지로 기울기를 계산했던 것의 지수 평균을 저장합니다.

Q8. GAN에 대해서 설명하라. 

GAN이란 크게 생성자(Generator)와 판별자(Discriminator)로 구성된 모델로 동시에 두 개의 모델을 훈련합니다. 생성자는 최대한 fake 이미지를 만들고 판별자는 최대한 fake 이미지를 탐지하도록 경쟁하는 구조입니다. GAN의 학습목표는 생성자가 생성한 이미지를 판별자가 맞출 확률이 1/2에 수렴하도록하여 진짜 이미지와 가짜 이미지를 구분할 수 없도록 하는 nash equilibrium을 찾는 것입니다. 

Q9. Auto Encoder에 대해 설명하라.

Auto Encoder는 크게 인코더와 디코더의 구조로 구성되어 있습니다. 인코더와 디코더의 중간에 있는 hidden layer는 Input layer보다 적은 수의 뉴런을 두는 bottleneck을 두어 차원을 줄여 압축하고 다시 디코더를 통해 압축된 데이터를 복원시키는 방식으로 동작합니다. 데이터를 압축하는 과정에서 추출한 의미있는 데이터를 보통 latent vector, z로 표현합니다. 즉 Auto Encoder는 학습을 통해 이 latent vector를 자동으로 추출해주는 모델이라 할 수 있습니다. 

Q11. ViT에 대해 설명하라.

ViT는 이미지를 16x16으로 나눠 트랜스포머에 아키텍처에 입력하는 모델입니다. CNN에서 사용하던 필터를 없애고 어텐션으로 대체했습니다. 이미지를 16x16 패치로 나누어 토큰화하여 트랜스포머 아키텍처에 입력합니다. 하지만 트랜스포머는 자연어처리를 위해 만들어진 아키텍처이기 때문에 CNN에 비해 *inductive bias가 부족했기에 기존 CNN을 사용하는 것보다 성능이 떨어졌습니다. 하지만 JFT-300M 데이터셋을 이용해 3억장의 이미지를 학습한 결과 CNN 보다 더 좋은 성능을 얻을 수 있었습니다. 

*inductive bias: 학습시 만나보지 못한 상황에 대해 정확히 예측하기 위해 사용하는 추가적인 가정. 

• CNN은 지역성(Locality)이란 가정을 활용해 공간적(spatial)인 문제를 해결함
• RNN은 순차성(Sequentiality)이란 가정을 활용해 시계열(time-series)인 문제를 해결함

Q12. Diffusion model에 대해 설명하라.

Diffusion model은 generative model 중 하나입니다. 컴퓨터 비전에서 사용됩니다. 데이터에 노이즈를 조금씩 추가해가면서 데이터를 완전한 노이즈로 만드는 forward process가 있고 이와 반대로 노이즈로부터 조금씩 복원해가면서 데이터를 만들어내는 reverse process가 있습니다. (추가 필요)

Q13. Batch Normalization에 대해 설명하라.

Batch Normalization은 activation function의 출력값을 정규화하는 방식입니다. 정규화를 위해 미니 배치마다 평균과 분산을 구해 표준정규분포를 따르도록 만들어주는 방식으로 동작합니다. 이러한 batch normalization이 필요한 이유는 입력 데이터마다 다양한 분포를 갖기 때문에 학습에 있어 모델의 일반화 성능을 가져오기 못하기 때문입니다. 만약 다양한 분포를 가진채로 학습하게 되면 gradient descent에 따른 업데이트 되는 weight에 영향력이 달라지기 때문입니다. 

2. Machine Learning

Q1. 앙상블 기법 종류와 특징에 대해 설명하라.

앙상블 기법은 크게 3가지로 보팅(Voting), 배깅(Bagging), 부스팅(Boosting)이 있습니다. 보팅은 여러 개의 분류기를 통해 최종 예측 결과를 결정합니다. 크게 하드 보팅과 소프트 보팅이 있습니다. 하드 보팅은 분류기의 예측 결과를 다수결 투표를 진행하는 것을 말하고 소프트 보팅은 분류기의 예측 결과의 확률값의 평균 또는 가중합 하는 것을 말합니다. 배깅도 보팅과 마찬가지로 여러 개의 분류기를 통해 나온 예측 결과값을 다수결 투표를 통해 결정하는 것을 말합니다. 차이점이 있다면 보팅은 서로 다른 분류기를 사용하고 배깅은 서로 같은 분류기를 사용해 다수결 투표를 진행하는 것입니다. 배깅의 대표적인 알고리즘은 랜덤 포레스트가 있습니다. 부스팅은 배깅과 비슷합니다. 다만 차이점이 있다면 배깅은 서로 같은 모델들이 독립적으로 학습하여 최종 예측 결과를 내지만 부스팅은 이전 모델의 결과를 기반으로 순차적으로 학습합니다. 가령 첫 번째 모델이 학습한 결과를 기반으로 두 번째 모델이 학습하고 두 번째 모델 결과를 기반으로 세 번째 모델이 학습하는 방식입니다. 이 때 학습 데이터의 샘플 가중치가 계속해서 조절되는 것이 특징입니다. 이러한 부스팅은 오답에 대해 높은 가중치가 부여될 수 있어 outlier에 취약하단 단점이 있습니다. 이러한 부스팅에는 XGBoost나, AdaBoost, GradientBoost과 같은 종류의 알고리즘이 있습니다.

Q2. 랜덤 포레스트에 대해 설명하라. (예상)

랜덤 포레스트는 앙상블 기법 종류 중 배깅 방식에 속하는 알고리즘입니다. 배깅 방식의 특징은 부트스트래핑을 통해 데이터를 랜덤 샘플링하는 과정이 있습니다. 랜덤 포레스트는 다수의 의사결정트리를 만들고 각각의 트리에서 랜덤 샘플링된 데이터를 학습한 다음 최종 예측 결과를 투표하는 방식으로 동작합니다. 또 랜덤 포레스트는 단일한 의사결정트리를 사용했을 때 오버피팅될 수 있다는 단점을 극복하기 위해 만들어진 것이기에 오버피팅을 감소시켜주고 비교적 일반화된 성능을 낼 수 있다는 장점이 있습니다.

Q3. XGBoost와 LightGBM에 대해 설명하라. (예상)

XGBoost와 LightGBM은 모두 앙상블 기법 종류 중 부스팅 방식에 해당하는 알고리즘입니다. 공통적으로 Gradient Boosting Machine에 기반한 방식입니다. XGBoost는 GBM의 3가지 단점을 개선했습니다. 첫 번째로 GBM은 병렬처리가 되지 않아 속도가 느렸다는 한계가 있었고 이를 해결하여 병렬처리를 통해 수행 속도를 빠르게 했습니다. 두 번째는 GBM에 Regularization 기능이 없어 오버피팅이 발생할 수 있단 한계가 있었지만 XGBoost는 자체적으로 Regularization 기능을 포함하고 있습니다. 세 번째로 Early Stopping 기능이 있다는 장점이 있습니다. Decision Tree 기반 알고리즘 중 성능이 우수하다고 알려져 있어 Kaggle과 같은 곳에서 많이 사용되고 있습니다. LightGBM은 XGBoost가 만들어지고 2년뒤에 만들어진 부스팅 알고리즘입니다. XGBoost가 GBM에 비해 빠르지만 여전히 학습 시간이 오래걸린다는 단점이 있습니다. 때문에 LightGBM은 이러한 XGBoost의 느린 학습 시간이라는 단점을 보완했고 또 메모리 효율성을 가져온 알고리즘입니다.

Q4. Gradient Descent에 대해 설명하라.

Gradient Descent는 cost function의 값이 최소가 되게 하는 가중치를 찾는 알고리즘입니다. 신경망에서 back-propagation을 위해 사용되며 cost function을 미분한 다음 learning rate를 곱해주고 체인룰을 적용해 앞단에 위치한 레이어의 가중치를 업데이트 하는 방식으로 동작합니다. 이 Gradient Descent 방식은 전체 데이터를 사용해 기울기를 계산하기 때문에 학습에 많은 시간이 필요하단 단점이 있습니다. 때문에 이런 단점을 보완하기 위해 미니 배치 사이즈로 나누어 학습을 진행하는 Mini-Batch Stochastic Gradient Descent 방식이 사용되기도 합니다.

Q5. Bias-Variance Trade-off에 대해 설명해주세요. (예상)

Bias는 under-fitting과 관련 있는 것으로 모든 데이터를 고려하지 못해 지속적으로 잘못된 것을 학습하는 경향입니다. 만약 Bias가 높으면 예측과 정답의 차이가 크게 벌어진 상황을 의미하고 Bias가 낮다면 예측과 정답이 차이가 작은 상황을 의미합니다. 반면 Variance는 over-fitting과 관련 있는 것으로 데이터 내에 노이즈까지 잘 잡아내어 실제 정답과 관련 없는 random한 것 까지 학습하는 경향을 의미합니다. variance가 높다는 것은 예측값과 정답값 간의 범위가 멀다는 것을 의미하고 variance가 낮다는 것은 예측값과 정답값 간의 범위가 좁다는 것을 의미합니다.

Q6. Training, Validation, Testing 셋으로 나누는 이유에 대해 설명하라. (예상)

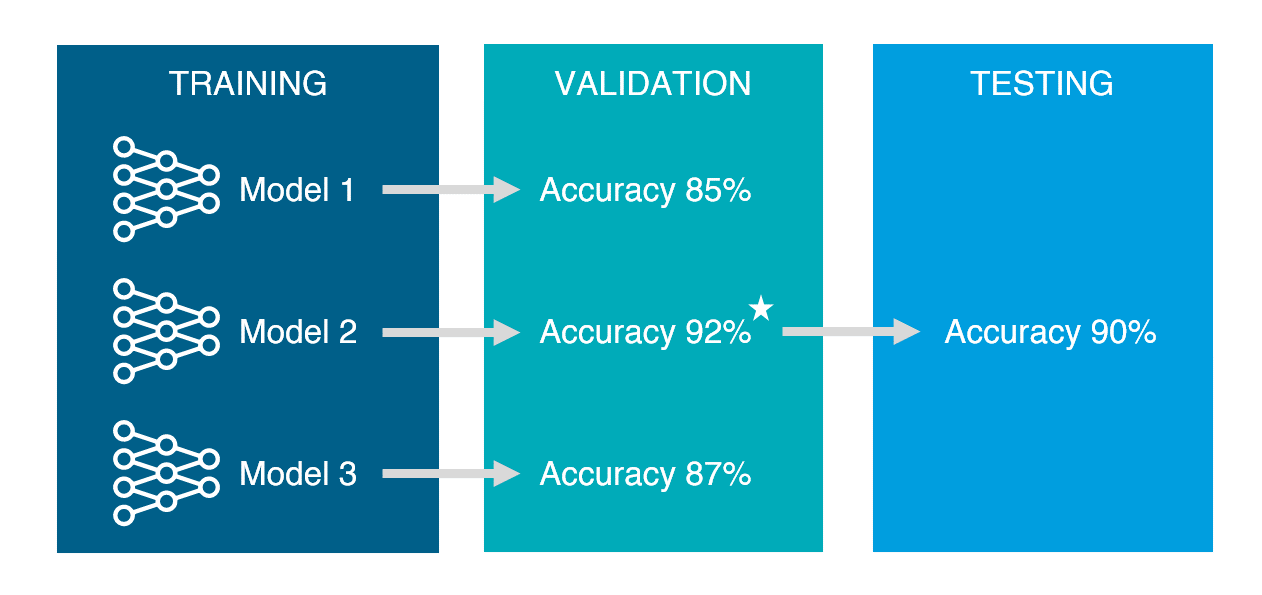
먼저 Training set은 모델 학습을 목적으로 사용합니다. 만약 training set을 평가에 사용한다면 이미 한 번 본 시험으로 재시험을 보는 것과 같기에 별도의 validation set이나 testing set으로 나누어 주어야 합니다. 이후 validation set의 경우 training set으로 만든 모델의 성능을 측정하기 위해 사용합니다. 이를 위해 다양한 모델과 파라미터를 사용해가며 validation set에 적합한 모델을 선택해야 합니다. 이후 마지막으로 testing set을 이용해 단 한번 모델의 성능을 측정하기 위해 사용합니다. 이후 training set, validation set, testing set을 모두 합쳐 다시 모델을 학습하여 최종 모델을 만듭니다. 간단한 비유를 하자면 training set은 월별 모의고사고 validation set은 그 중에서도 9월 모의고사처럼 실제와 비슷할 것이라 판단되는 모의고사이며 마지막 testing set을 통해 수능을 보는 것과 같습니다. 

Q7. K-fold cross validation에 대해 설명하라. (예상)

K-fold cross validation이란 전체 데이터에서 training set과 validation set을 번갈아가며 나누는 방법을 의미합니다. 예를 들어 전체 데이터를 5분할을 한다면 처음엔 가장 첫 번째 분할을 validation set으로 두고 나머지 네 개의 분할을 training set으로 두고 두 번째 학습에는 두 번째 분할을 validation set으로 두고 나머지 분할을 training set으로 두는 것과 같습니다. 이렇 게 하는 이유는 데이터셋의 크기가 작을 경우 validation set에 대한 성능평가 신뢰성이 떨어지기 때문입니다. 즉 특정 validation set에만 적합한 모델을 피하고 전체 데이터셋에 균형 잡힌 학습을 위해 사용합니다.

3. Probability/Statistics

Q1. Posterior, Prior, Likelihood에 대해 설명하라.

이 세 개의 개념은 베이즈 정리에 사용됩니다. 베이즈 정리란 Prior, Likelihood, Evidence를 통해 Posterior를 예측하는 방법입니다. Prior는 사전에 이미 알고 있는 확률을 뜻하고 Posterior는 새로 추정된 확률을 뜻합니다. Likelihood는 Probability와 대조적인 특징이 있습니다. Probability는 확률분포를 이미 알고 있다는 가정하에 확률변수값이 계산됩니다. 반면 Likelihood는 확률과달리 확률분포를 모른다는 가정하에 주어진 관측을 통해 확률분포를 추정해나가는 방식입니다. Probability는 특정 사건 발생확률을 더하면 1이될 수 있지만 Likelihood는 그렇지 않습니다. 즉 요약하면 사전확률과 가능도와 새로 관측된 데이터를 통해 사후확률을 계산하는 것이 베이즈 정리입니다. 이 베이즈 정리는 조건부 확률에 기반하며 손쉽게 유도가능합니다.

Q1-1. 베이즈 정리 예시를 설명해라.

Q2. Hidden Markov Chain에 대해 설명하라.

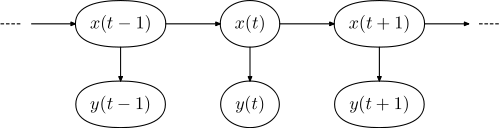
히든 마르코프 체인의 경우 마르코프 체인을 기반으로 합니다. 마르코프 체인이란 마르코프 성질을 가진 이산확률과정입니다. 마르코프 성질이란 미래 상태는 현재 상태에 의해 결정되는 성질입니다. 즉 인과성이 있다는 것입니다. 또 이산확률과정이란 시간의 흐름에 따라 확률적인 변화를 가지는 구조를 의미합니다. 마르코프 성질의 대표적인 예시로는 날씨 예측이 있고 아닌 예시로는 매 번 독립 시행인 동전던지기가 있습니다. 히든 마르코프 체인의 경우 이러한 마르코프 체인에서 확장된 것으로 시스템이 은닉 상태와 관찰 가능한 결과 두 가지의 요소로 이뤄진 모델입니다. 관찰 가능한 결과는 은닉 상태에 의해 결정되지만 은닉 상태는 직접적으로 볼 수 없습니다. 오로지 마르코프 과정을 통해 도출된 결과만 관찰할 수 있습니다. 이런 히든 마르코프 체인은 주로 시퀀셜한 데이터를 다루는데 강점이 있습니다.

Q3. Entropy, Cross entropy, KL-divergence에 대해 설명하라.

entropy는 불확실성을 뜻하는 것으로 확률분포에서 확률변수 X의 기대값을 의미합니다. 수식으로는 $\displaystyle H(x) = -\sum_{i=1}^n p(x_i)\log p(x_i)$로 정의할 수 있습니다. cross entropy 같은 경우엔 entropy가 단일 확률분포에서 어떤 확률변수가 나타날 불확실성이었으면 cross entropy는 두 확률분포 간의 차이를 나타내는 척도라고 할 수 있습니다. 수식으로는 $\displaystyle H_{p, q}(x) = -\sum_{i=1}^n p(x_i)\log q(x_i)$로 나타냅니다. 마지막으로 KL-divergence는 두 확률분포 간의 차이를 나타내는 척도입니다. cross-entropy에서 entropy를 뺀 값이며, 수식으로는 $\displaystyle KL(p||q) = \sum_{i=1}^n p(x) \log {p(x)\over q(x)}$로 나타냅니다. 사실상 cross entropy와 거의 동일해 KL-divergence를 최소화 하는 것은 cross entropy를 최소화 하는 것과 같습니다. 하지만 KL-divergence에 있는 $p(x)\log p(x)$는 모델이 예측하고자 하는 실제 모집단분포이므로 바뀌지 않고 알 수 없는 값입니다. 따라서 cost function으로 사용하려면 상수 취급되어 계산에 포함하지 않아야 합니다. 그러면 남는 것은 $\displaystyle -\sum_{i=1}^n p(x_i) \log q(x_i)$이고 이는 곧 cross entropy를 의미합니다.

Q4. 정규분포에 대해 설명해주세요. (예상)

정규분포는 여러 확률분포함수 중에서 연속확률분포에 속하는 분포입니다. 수식은 $\displaystyle f(x) = {1 \over \sqrt{2\sigma^2}} \exp (- {(x-\mu)^2 \over 2\sigma^2})$로 나타냅니다. 이 정규분포는 평균과 분산 값에 따라 다양한 정규분포를 갖게 됩니다. 그 중 평균이 0, 분산이 1인 정규분포를 표준정규분포라 합니다. 이런 정규분포의 특징은 평균을 기준으로 대칭성을 띤다는 것입니다. 따라서 평균 기준 왼쪽과 오른쪽은 각각 0.5의 확률을 같습니다. 또 정규분포별 평균과 분산이 다르더라도 표준편차 구간 별 확률은 어느 정규분포에서나 같다는 것입니다. 

Q5. 이항분포에 대해 설명해주세요. (예상)

이항분포는 베르누이 시행을 n번 시행한 것 입니다. 어떤 사건 A가 발생할 확률이 p일 때 베르누이 시행을 n번 시행한다면 사건 A가 몇번 발생하는지를 확률변수로 두는 분포입니다. 수식으로는 $\displaystyle {}_n C{}_r p^r (1-p)^{n-r}$로 표현합니다. 평균 $E(x)$는 $np$입니다. 또 분산 $V(x)$는 $np(1-p)$입니다. 가장 흔한 예시로는 주사위를 n번 던졌을 때 특정 숫자가 나올 확률이 어떻게 되는가를 구할 때 사용합니다. 특정 숫자가 나올 확률은 ${1 \over 6}$ 이므로 $\displaystyle {}_n C {}_r {1\over 6}^r {5\over 6}^{n-r}$로 나타낼 수 있습니다. 

Q5. 균등분포의 역함수로 샘플링하는 샘플링 기법은 무엇인가? (Box-Muller Transformation에 대해 설명하라)

Q6. 공분산 행렬과 상관 계수에 대해 설명해주세요.

4. Reinforce Learning

Q1. 벨만 방정식에 대해 설명하라.

벨만 기대 방정식은 강화학습에 사용됩니다. 벨만 기대 방정식은 현재 상태의 가치함수와 다음 상태의 가치함수 사이의 관계를 나타낸 식입니다. 여기서 가치함수란 에이전트가 다음 상태로 갈 경우 앞으로 받을 전체 보상에 대한 기대값입니다. 가치함수는 현재 에이전트의 정책에 의해 영향을 받는데, 이 정책을 반영한 식이 벨만 기대 방정식이라 합니다. 정의상 기대값을 알려면 모든 보상에 대해 고려해야하지만 물리적으로 불가능 하므로 하나의 변수를 두고 그 변수를 계속해서 업데이트하는 과정으로 계산됩니다. (추가 필요)

Q2. DQN에 대해 설명하라. 또 DQN의 수식의 의미를 설명하라.

5. Computer Science

Q0. 프로세스와 쓰레드의 차이는 무엇인가?

Q0. 쓰레드의 특징은 무엇인가?

Q1. 캐시는 왜 사용하는가?

캐시를 사용하는 핵심 이유는 CPU 처리속도와 메모리 처리속도 차이에서 발생하는 병목현상을 해결하기 위해 사용합니다. 주기억장치인 메모리에 있는 데이터에 접근하는 시간을 줄이기 위해 CPU와 메모리 사이에 캐시 메모리를 둡니다. 캐시 메모리에는 주기억장치 내에서 자주 읽고 쓰는 데이터의 일부를 캐시 메모리에 불러와 속도 차이를 줄입니다. 그리고 캐시 메모리에는 적중률이라는 개념이 있습니다. CPU가 메모리에 접근하기 전에 캐시 메모리에 먼저 원하는 데이터가 존재하는지 여부를 확인하는데 이 때 있다면 적중한 것이고 없다면 실패한 것입니다. 캐시 메모리를 효율적으로 활용하기 위해서는 적중률이 높아야하고 이를 위해 지역성이라는 개념을 사용합니다. 크게 시간적 지역성, 공간적 지역성, 순차적 지역성 세 가지가 있습니다. 시간적 지역성은 최근 액세스된 메모리 영역은 근 미래에 다시 액세스할 가능성이 높다는 것을 뜻하고, 공간적 지역성은 CPU가 참조한 데이터와 인접한 영역에 있는 데이터 역시 참조될 가능성이 높음을 의미합니다. 마지막으로 순차적 지역성은 메모리에 데이터가 저장된 순서대로 이용될 가능성이 높다는 것입니다. 

Q2. vCPU란 무엇인가?

클라우드 환경에서 만들어지는 가상화 머신에 할당되는 형태의 CPU를 말합니다. 실제 물리적인 CPU 코어를 논리적으로 분할하여 가상화 머신에 할당하는 형태입니다.

Q3. HDD, SSD, DRAM의 차이는 무엇인가? 

핵심 차이는 속도라고 할 수 있습니다. DRAM이 가장 빠르고 SSD가 그다음 HDD가 마지막입니다. DRAM은 Dynamic Random Access Memory로서 RAM의 한 종류입니다. 이외의 종류는 Static Random Access Memory인 SRAM이 있습니다. SRAM은 속도가 빨라 캐시로 사용되고 DRAM은 속도가 상대적으로 느린 대신 용량이 크다는 특징이 있습니다. SSD Solid State Drive의 약자로 비휘발성 저장장치 입니다. 물리적으로 데이터가 위치하는 원판까지 플래터를 이동시켜야하는 HDD와 달리 전자적으로 정보를 읽고 쓰기 때문에 속도가 빠르다는 장점이 있습니다. 

Q4. 가상 메모리를 왜 사용 하는가?

가상 메모리를 사용하는 핵심 이유는 과거 메모리 용량의 한계가 있던 때, 메모리 크기보다 큰 프로세스를 실행시키기 위한 방법이 필요했습니다. 때문에 이를 해결하고자 디스크에서 프로세스 실행에 필요한 부분만 메모리에 적재하고 실행시킬 수 있도록 한 것입니다. 이 가상 메모리를 구현하기 위해서는 MMU라는 Memory Management Unit이 필요합니다. MMU는 가상 메모리에 사용되는 가상 주소를 실제 물리 주소로 매핑해주는 역할을 합니다. 이 때 모든 가상 주소를 물리 주소로 바꾸려면 많은 부하가 생길 수 있으므로 메모리를 페이지라는 단위로 나누어 효율적으로 처리합니다. 

Q5. 페이지 폴트란 무엇입니까? (예상)

페이지 폴트란 CPU가 프로세스 실행에 필요한 단위인 페이지를 요청 할 때 그 페이지가 실제로 메모리에 적재되어 있지 않을때 발생하는 인터럽트입니다. 만약 페이지 폴트가 발생하면 운영체제는 필요로 하는 페이지를 메모리로 가져와서 실행함으로써 마치 페이지 폴트가 발생하지 않은 것처럼 합니다. 이 때 페이지 폴트가 자주 일어나면 오버헤드로 인해 컴퓨터 성능이 저하될 수 있으므로 페이지 폴트를 최소화하기 위해 여러 페이지 교체 알고리즘을 사용합니다. 

Q6. 스래싱(Trashing)에 대해 설명하라. (예상)

쓰래싱은 어떤 프로세스에 지속적으로 페이지 폴트가 발생하는 현상을 의미합니다. 달리 말해 페이지 폴트율이 높아져 프로세스 처리시간보다 페이지 교체시간이 더 많이 발생하는 현상입니다. 이러한 스래싱 현상을 해결하기 위해 크게 두 가지로 Page-Fault Frequency(PFF)와 워킹셋(Working Set)을 사용합니다. 먼저 페이지 폴트율을 주기적으로 계산해서 각 프로세스에 할당할 메모리 양을 동적으로 조절합니다. 만약 어떤 threshold를 넘으면 프로세스에 할당된 프레임이 부족하다 판단하고 프로세스에게 프레임을 추가로 할당합니다. 만약 할당할 빈 프레임이 없을 경우 일부 프로세스를 스왑아웃 시켜 할당합니다. 반면 어떤 threshold이하일 경우 프로세스에게 많은 프레임이 할당된 것으로 판단해 할당된 프레임의 수를 줄입니다. 만약 모든 프로세스에 필요한 프레임을 다 할당한 뒤에도 여유 공간이 있다면 스왑 아웃되어 있던 프로세스를 스왑 인하여 다중프로그래밍정도인 MPD를 높입니다. 

워킹셋은 프로세스가 실행되기 위해 한 번에 메모리에 올라와있어야 할 페이지의 집합을 의미합니다. 워킹셋 알고리즘을 통해 이러한 페이지 집합을 결정할 수 있습니다. 또 프로세스의 워킹셋이 한 번에 메모리에 올라갈 수 있는 경우에만 프로세스에게 메모리를 할당합니다. 그렇지 않은 경우 프로세스에게 할당된 페이지 프레임을 모두 반납하구 프로세스 주소 공간 전체를 디스크로 스왑 아웃시킵니다.

Q7. 페이지 스와핑에 대해 설명해주세요. (예상)

페이지 스와핑은 중기 스케쥴러에 의해 처리됩니다. 페이지 스와핑은 크게 페이지 스왑 인과 페이지 스왑 아웃으로 나뉩니다. 페이지 스왑 인의 경우 프로세스가 실행될 때 페이지 폴트가 발생할 경우 페이지를 메모리에 추가 적재하기 위해 사용합니다. 반면 페이지 스왑 아웃의 경우 워킹셋 알고리즘이 동작할 때 처럼 특정 페이지셋이 한 번에 메모리에 적재되기에 공간이 충분하지 않을 때 디스크 영역으로 옮기는 것을 말합니다.

Q8. 페이지 교체 알고리즘에 대해 설명하라.

페이지 교체는 메모리에 적재할 공간이 부족할 때 메모리에 적재된 프로세스를 디스크로 스왑 아웃하고 프로세스 실행에 필요로 하는 페이지를 메모리에 적재하는 것입니다. 이러한 페이지 교체 알고리즘의 목표는 Page-Fault Frequency를 최소화하는 것입니다. 이런 알고리즘의 종류는 FIFO, LRU, LFU, 빌레디, 클럭등이 있습니다. (추가 설명 필요)

Q9. 페이징의 장단점은 무엇인가?

페이징은 외부 단편화 문제를 해결하기 위해 사용하는 메모리 관리 기법입니다. 외부 단편화는 여분의 메모리 공간이 요청한 메모리 공간보다 커서 여유가 있지만 여유 공간이 연속적이지 않아 발생하는 현상입니다. 페이징은 페이지라는 단위로 메모리 공간에 불연속적으로도 적재할 수 있도록 합니다. 이처럼 페이징을 이용하면 외부 단편화 문제를 해결하는 장점이 있지만 반면 내부 단편화 문제가 발생하는 단점이 있습니다. 내부 단편화란 한 마디로 공간 낭비라 설명할 수 있습니다. 외부 단편화와 달리 메모리 공간에 프로세스 실행에 필요한 데이터가 적재될 공간이 충분히 있고 적재될 수 있지만 적재되고 나서 빈 영역이 발생하는 것입니다.

Q10. 세그멘테이션의 장단점은 무엇인가?

페이징 기법이 가지는 내부 단편화 문제를 극복하기 위해 세그멘테이션 기법이 사용됩니다. 페이지는 기본적으로 4KB 단위로 만들어집니다. 때문에 만약 9KB짜리 프로세스를 실행해야 한다면 메모리 공간에 12KB가 할당되고 3KB의 사용되지 못하고 낭비되는 영역이 만들어집니다. 세그멘테이션은 페이징과 똑같이 메모리 관리 기법이지만 차이점은 분할 방식입니다. 페이징은 한 단위를 기준으로 정적으로 분할하지만 세그멘테이션은 동적으로 분할하여 내부 단편화가 발생하지 않도록 합니다. 하지만 이런 세그멘테이션은 내부 단편화를 해결한다는 장점이 있지만 페이징에 비해 상대적으로 복잡한 메모리 관리로 오버헤드가 발생할 수 있다는 단점이 있습니다.

Q11. 임계 영역에 대해 설명하라.

임계 영역은 둘 이상의 쓰레드가 공유자원에 접근하는 데 있어 한 번에 한 쓰레드만 접근할 수 있도록 보장하는 영역을 말합니다. 임계 영역을 둠으로써 쓰레드는 공유자원에 대한 배타적인 사용권을 보장받을 수 있습니다. 이러한 임계 영역을 두기 위해 사용하는 방법으로 크게 뮤텍스와 세마포어가 있습니다.

Q12. 뮤텍스(Mutal Exclusion, Mutex)와 세마포어(Semaphore)의 차이를 설명하라.

뮤텍스 즉 상호배제란 임계 영역에 접근하는 쓰레드 간의 충돌을 막기 위해 사용하는 기법입니다. 이를 위해 Lock을 사용해서 임계영역에 들어가는 쓰레드가 Lock을 걸어 다른 쓰레드가 임계 영역으로 들어오지 못하도록 하고 이후 나갈 때 Lock을 해제하는 방식으로 다른 쓰레드가 임계 영역으로 들어올 수 있도록 하는 방법입니다. 세마포어 또한 임계 영역에 접근하는 쓰레드 간의 충돌을 막기 위해 사용하는 기법입니다. 기본적으로 뮤텍스와 동일하지만 차이점이 있다면 뮤텍스는 임계 영역에 들어간 쓰레드가 Lock을 걸고 해제할 수 있는 Locking 메커니즘을 사용하는 반면 세마포어는 Lock을 걸지 않은 쓰레드도 Lock을 해제할 수 있는 Signaling 메커니즘을 사용합니다.

Q13. 스케쥴링에 대해 설명하시오.

스케쥴링은 프로세스를 실행시키기 위해 CPU의 자원을 할당하는 정책을 계획하는 것입니다. 이 CPU 스케쥴링이 필요한 이유는 CPU 자원을 프로세스에게 효율적으로 할당하여 더 많은 작업을 처리할 수 있는 처리 속도를 높이기 위함입니다. 스케쥴링 방식에는 크게 선점형 스케쥴링과, 비선점형 스케쥴링이 있습니다. 선점형 스케쥴링은 한 프로세스가 CPU를 할당받아 실행되고 있을 때 우선순위가 다른 프로세스가 CPU를 강제로 점유할 수 있도록하는 기법입니다. 종류로는 라운드로빈, SRT ,다단계 큐, 다단계 피드백 큐 등의 알고리즘이 있습니다. 반면 비선점형 스케쥴링은 한 프로세스가 CPU를 항당받아 실행되고 있을 때 다른 우선 순위높은 프로세스가 CPU를 강제로 빼앗아 점유할 수 없는 기법입니다. 종류로는 FCFS, SJF, HRN 등의 알고리즘이 있습니다.

Q13-1. 스케쥴링 알고리즘에 대해 설명해주세요. (예상)

FCFS(First-Come First-Served)는 큐에 먼저 도착한 프로세스 순서대로 스케쥴링 하는 방식입니다. 비선점 스케쥴링에 방식에 해당합니다. 이런 FCFS의 단점은 CPU를 장기간 독점하는 프로세스가 있다면 다른 프로세스가 실행되지 못하고 오래 기다려야 한다는 단점이 있습니다. 이러한 단점을 보완하기 위해 SJF(Shortest-Job-First) 기법이 사용됩니다. CPU 작업시간이 짧은 프로세스 순서대로 스케쥴링하는 방식입니다. 비선점 스케쥴링 방식에 해당합니다. 특징은 만약 CPU 작업시간이 동일할 경우 FCFS 정책을 따릅니다. 이 SJF의 장점은 프로세스의 평균 대기 시간이 최소화된다는 것이며 단점은 CPU 작업시간에 대한 정확한 계산이 가능하지 않고, CPU 작업 시간이 긴 프로세스는 오랜시간 CPU를 할당받지 못할 수 있습니다. FCFS와 동일하게 이런 점유 불평등 현상이 있는 SFJ 알고리즘을 보완하기 위해 우선순위를 기반으로하는 HRN(Highest Response-ratio Next) 방식이 사용됩니다. 우선 순위는 $(대기시간 + 실행시간) \over (실행 시간)$로 계산 됩니다. 이외에도 여러 스케쥴링 알고리즘이 있지만 가장 일반적으로 사용하는 것은 Round Robin입니다. RR은 FCFS와 마찬가지로 순차적으로 스케쥴링을 진행하지만 특징은 동일한 시간의 Time Quantum만큼 CPU를 할당해 프로세스를 실행하는 방식입니다. RR 방식은 공정하다는 장점이 있지만 반면 Time Quantum이 커지면 FCFS와 같아진다는 단점이 있고, 작다면 Context Switcing이 많아져 오버헤드가 증가하는 단점이 있습니다.

Q14. Context Swiching에 대해 설명하라. (예상)

CPU가 어떤 프로세스를 실행 중일 때 인터럽트에 의해 다른 프로세스를 실행시켜야 하는 경우 기존 실행되던 프로세스 상태를 PCB에 저장하고 새로운 프로세스를 메모리에 적재하는 방법입니다. Context Swiching이 되면 실행될 프로세스의 PCB에 있는 정보와 레지스터 값을 읽어온 다음 이어서 작업을 수행합니다. 이 Context Swiching이 많이 일어나면 오버헤드가 발생하므로 Context Switching을 일으키는 스케쥴러가 최소한으로 Context Swiching이 일어나도록하는 스케쥴러 알고리즘을 사용해야 합니다.

Q15. Call By Value와 Call By Reference의 차이에 대해 설명하시오.

Call By Value란 Call By Reference는 함수에 인자를 전달하는 두 방식입니다. Call By Value는 전달받은 인자를 함수 내에서 복사해서 사용하는 것을 의미합니다. 복사해서 사용하기 때문에 원래 값에 영향을 미치지 않습니다. 반면 Call By Reference는 메모리 주소값에 있는 값을 직접 참조하는 방식입니다. 따라서 원래 값에 영향을 미치는 방식입니다. 

Q16. PNG와 JPG의 차이를 설명하라.

Q17. 다이나믹 프로그래밍이란 무엇인가? 또 신경망의 관점에서는 어떻게 활용되는가?

DP는 큰 문제를 작은 문제로 나누어 푸는 방법입니다. 분할정복 알고리즘과 같이 큰 문제를 작은 문제로 나누어 푼다는 점에서 공통점을 가집니다. 하지만 차이점은 작은 문제 계산에 있어 반복이 일어나지 않는다는 것입니다. 일반적으로 DP는 점화식을 세워 문제를 해결합니다. 또 memoization을 이용해 한 번 계산해둔 값을 다시 활용한다는 특징이 있습니다. 가장 쉬운 예시로는 피보나치 수열이 있습니다. 즉 다음 수열의 값은 현재 수열 값과 이전 수열 값의 합입니다. 1, 1, 2, 3, 5, 8로 증가하는 형태를 가지며 다음 수열을 구할 때 이미 구해두었던 수열의 값을 활용합니다.

신경망의 관점에서 역전파를 진행할 때 다이나믹 프로그래밍을 사용합니다. back-propagation하면서 gradient를 전부 계산하는 것이 아니라 마지막 출력노드에서 한 번 미분값을 계산한 뒤 backward 방향의 노드로 전달하면서 재사용합니다.

Q18. 백트래킹 알고리즘에 대해 설명하라.

백트래킹 알고리즘이란 해를 찾는 도중 해가 아니라고 판단될 경우 되돌아가서 다시 해를 찾는 방법입니다. 백트래킹 알고리즘은 일반적으로 DFS와 함께 사용됩니다. DFS는 알고리즘은 가능한 모든 경로를 탐색하기 때문에 계산 비용이 많이 발생합니다. 이를 해결하기 위해 가지치기가 필요한데 이 때 사용하는 것이 백트래킹 알고리즘입니다. 대표적인 예제로 N-Queen 문제가 있습니다. 

Q19. 거의 정렬이 이뤄졌을 때 사용하면 좋은 정렬 알고리즘은 어떤 것인가?

삽입 정렬을 사용하면 좋습니다. 삽입 정렬은 정렬할 원소보다 index가 낮은 곳에 있는 원소들을 탐색해 정렬하는 알고리즘 입니다. 동작은 두 번째 index에 있는 원소부터 시작합니다. 삽입 정렬의 특징은 알고리즘이 동작하는 동안 반드시 맨 왼쪽 index까지 탐색하지 않아도 됩니다. 앞 부분은 이미 정렬 되어 있기 때문에 정렬 하고자 하는 원소보다 작아지는 경우 다음에만 삽입하면 됩니다. 거의 정렬이 모두 이뤄져있다면 모든 원소가 한 번씩만 비교하므로 $O(n)$의 복잡도를 가집니다.

Q20. 대칭키 암호화와 비대칭키 암호화는 무엇인가?

대칭키 암호화는 암복호화에 사용하는 키가 동일한 방식의 암호화입니다. 종류로는DES, 3DES, AES, SEED, ARIA 등이 있습니다. 장점으로는 비대칭키 암/복호화에 비해 수행 시간이 짧습니다. 반면 키교환문제가 발생한다는 단점이 있습니다. 비대칭키 암호화는 암복호화에 사용하는 키를 서로 달리하는 방식의 암호화입니다. 종류로는 RSA, ElGamal, ECC 등이 있습니다. 장점은 공개키가 있고 개인키가 있기 있기 때문에 키 교환 문제가 발생하지 않습니다. 단점은 대칭키에 비해 암복호화 수행시간이 느리다는 것이 있습니다.

Q20-1. 비대칭키는 왜 공개키와 비밀키로 나뉘는가?

키교환 문제를 해결하기 위해 사용합니다. 대칭키는 암호화와 복호화에 사용하는 키가 같기 때문에 이 키를 전달하는 과정에서 탈취될 가능성이 존재합니다. 반면 비대칭키는 공개키가 공개되어 있기 때문에 키교환 문제가 발생하지 않습니다. 동작방식은 가령 A와 B가 있을 때 B가 공개키/개인키 쌍을 생성합니다. A는 전달하고자 하는 정보를 B의 공개키로 암호화해서 B에게 주면 B는 자신의 개인키를 이용해 복호화를 수행하는 방식으로 이루어집니다.

Q21. TCP/UDP 차이를 설명하라.

TCP는 연결지향형 프로토콜이고 UDP는 비연결지향형 프로토콜입니다. 연결지향형이랑 클라이언트와 서버가 연결된 상태에서 데이터를 주고 받습니다. 반면 비연결지향형은 클라이언트와 서버가 연결되지 않은채로 데이터를 일방적으로 전송합니다. TCP를 사용하기 위해서는 3-way handshaking 과정을 거쳐야 합니다. 클라이언트는 SYN 플래그를 보내면 서버는 SYN + ACK를 보내고 다시 클라이언트는 ACK를 보냄으로써 상호 연결됩니다. 이러한 TCP의 특징은 데이터의 전송순서를 보장하고 수신여부를 확인합니다. 때문에 신뢰성이 높다는 장점이 있습니다. 반면 UDP보다 데이터 전송속도가 느리다는 단점이 있습니다. UDP는 3-way handshaking 과정 없이 데이터를 일방적으로 전송합니다. UDP의 특징은 데이터의 전송 순서가 보장되지 않으며 수신 여부를 확인하지 않습니다. 따라서 신뢰성이 낮다는 단점이 있습니다. 반면 TCP에 비해 속도가 빠르다는 장점이 있습니다.

Q22. 공유기 동작은 어떻게 이루어지는가?

공유기에 LAN 선을 연결하게 되면 공인 IP가 부여됩니다. 이 공유기에 장치를 연결하면 NAT에 의해 공인 IP가 사설 IP로 변경되어 할당됩니다. 공인 IP는 외부 인터넷과 연결을 위해 사용하고 사설 IP는 내부 인터넷 사용을 위해 사용합니다. 내부 인터넷에서 외부 인터넷으로 연결하기 위해서는 NAT를 통해 다시 공인 IP로 변경됩니다. 이 때 연결 요청이나 자원 요청에 대한 응답을 받기 위해서는 PAT를 통해 사설 IP에 할당된 포트정보까지 매핑시킴으로써 특정 디바이스를 식별할 수 있습니다. 만약 내부의 요청 없이 곧 바로 외부에서 내부로 접근하기 위해서는 포트포워딩을 통해 접속할 수 있습니다. 

Q23. RESTful에 대해 설명하라. 또 단점은 무엇인가? 

REST는 HTTP 프로토콜을 통해 DB에 Create, Read, Update, Delete 연산을 수행하는 것을 의미합니다. client-server 구조를 갖는게 REST의 특징 중 하나입니다. 하지만 클라이언트가 직접 DB에 접근하는 것을 위험하므로 REST API를 두어 서버가 데이터베이스에 클라이언트의 요청을 수행하고 결과를 반환합니다. 이러한 요청을 위해 HTTP METHOD를 사용하며 종류로는 GET, POST, PUT, DELETE 등이 있습니다. RESTful은 이러한 REST 아키텍처의 특징을 잘 지켜 설계한 것을 의미합니다. "REST API를 제공하는 웹 서비스는 RESTful하다"와 같이 표현할 때 사용됩니다. 이러한 REST 또는 RESTful의 장점은 쉽게 사용할 수 있다는 것입니다. REST API 메시지를 읽는 것만으로 의도하는 바를 명확히 파악할 수 있습니다. 반면 표준이 존재하지 않는다는 단점이 있습니다.

Q24. NoSQL의 장단점을 이야기하라.

NoSQL은 일반적으로 RDBMS와 함께 언급됩니다. 먼저 NoSQL의 장점은 정해진 스키마가 없기 때문에 데이터 구조가 유연하고 자유롭게 컬럼을 추가할 수 있습니다. 또 대용량 처리에 적합합니다. 반면 단점으로는 정해진 스키마가 없기 때문에 데이터의 일관성이 없습니다. 또 중복이 발생할 수 있고 발생할 경우 계속해서 모든 컬렉션에서 업데이트해야하는 번거로움이 있습니다. RDMBS의 장점은 정해진 스키마가 있기 때문에 데이터 구조의 일관성이 보장됩니다. 또 데이터의 중복이 발생하지 않습니다. 반면 단점으로는 정해진 스키마가 있기에 유연성이 떨어집니다. 또 규모가 커질수록 테이블 간 JOIN이 복잡해지고 쿼리 프로세싱도 복잡해져 성능이 저하됩니다. 

Reference

[1] [운영체제] 페이징과 세그멘테이션 (제이온)

[2] [OS] 세마포어(Semaphore) vs 뮤텍스(Mutex) 차이 (망나니개발자, MangKyu)

[3] [운영체제] CPU 스케줄링이란? (그적)

[4] [운영체제] CPU 스케줄링 (제이온)

[5] [운영체제OS]8. 가상메모리(페이징, 페이지 교체, 스레싱)

[6] 알고리즘 - Dynamic Programming(동적프로그래밍)이란? (전준엽)

[7] [암호학] 대칭키 vs 공개키(비대칭키) 암호화 차이 (leeforest)

[8] [Network] TCP / UDP의 개념과 특징, 차이점 (코딩팩토리)

[9] 랜덤 포레스트(Random Forest) 쉽게 이해하기 (아무튼 워라밸)

[10] [ML] XGBoost 개념 이해 (최우노)

[11] 벨만 방정식 (subsay)

[12] Training, Validation and Test sets 차이 및 정확한 용도 (훈련, 검정, 테스트 데이터 차이) (네이쳐k)

[13] 딥러닝 모델의 K-겹 교차검증 (K-fold Cross Validation) (DEEPPLAY)

[14] Hidden Markov Model (은닉 마르코프 모델) (Bioinformatics And Me)

[15] 인공지능의 이해 (5/6): 순환 신경망 (RNN) (라인하트)

[16] [딥러닝][NLP] LSTM(Long Short Term Memory Networks) (Hyen4110)

[17] Long Short-Term Memory (LSTM) 이해하기 (개발새발로그)

[18] CNN (Convolutional Neural Network) 개념 (강성욱)

[19] 배치 정규화(Batch Normalization)

문제 정의

문제의 핵심은 홀수인 자연수 N이 주어지면, 1부터 $N^2$까지의 자연수를 아래와 같이 달팽이 모양으로 $N * N$의 표에 채우라는 것이다.

입력

첫째 줄에 홀수인 자연수 N(3 ≤ N ≤ 999)이 주어진다. 둘째 줄에는 위치를 찾고자 하는 N2 이하의 자연수가 하나 주어진다.

출력

N개의 줄에 걸쳐 표를 출력한다. 각 줄에 N개의 자연수를 한 칸씩 띄어서 출력하면 되며, 자릿수를 맞출 필요가 없다. N+1번째 줄에는 입력받은 자연수의 좌표를 나타내는 두 정수를 한 칸 띄어서 출력한다.

접근 방법

알고리즘을 처음 접하는 입장으로써 주위 개발자에게 조언을 구했다. 처음엔 코드를 작성하면서 변수를 생각했다. 하지만 이것은 비효율적인 방법이라고 한다. 머리로 사용할 변수들을 최대한 미리 생각하고 이후에 필요에 따라 추가/제거 하는 것이 중요하다. 

1. 먼저 문제에서 바로 확인할 수 있는 변수 두 개인 홀수 자연수를 N으로 두고, 찾아야 할 값을 want로 선언하였다.

2. 찾아야 할 값 want의 2차원 좌표를 나타낼 변수를 x, y로 선언하였다.

3. 2차원 배열을 다루기 위해 사용되는 행렬을 row, col로 선언하였다.

4. 그리고 핵심이 되는 것은 dir(direction)이라는 방향을 나타내는 변수이다.

dir은 위와 같은 흐름으로 2차원 배열 변수에 값을 담기 위한 변수이다. dir을 1 또는 -1로 설정하여 row와 col에 더해줄 것이다. dir을 1로 설정하여 row에 더해줄 경우 자연스럽게 row가 증가하고, col에 더해줄 경우 col이 증가한다. 이후 dir을 -1로 설정하면 row가 감소하고, col이 감소한다. 이후 다시 dir을 1로 설정하면 row가 증가하여 최종적으로 1에 도달하는 식이다. (위 그림에 맞대어 row와 col에 dir을 더해주는 것을 시뮬레이션 해볼 것을 권한다. 이것이 문제 풀이의 핵심이다)

작성 코드

#include <iostream>
#include <cstring>

using namespace std;

int main(void)
{
	// 1. 변수 선언부
	int N = 0; // 입력 받을 홀수 자연수
	int want = 0; // N^2 이하의 찾고자 하는 자연수
	int x = 0, y = 0 ; // Want의 좌표를 나타낼 x, y 값
	int row = -1, col = 0;; // 달팽이를 나타낼 행, 열
	int dir = 1; // 방향을 나타낼 변수
	cin >> N;
	int copy = N;
	cin >> want;
	int squared = N * N; // N^2을 표현할 변수

	int** arr;
	arr = new int* [N]; // 2차원 배열의에서 사용할 배열의 길이(row)

	for (int i = 0; i < N; i++)
	{
		arr[i] = new int[N]; // N = 2차원 배열에서 사용할 배열의 길이(column)
		memset(arr[i], 0, sizeof(int)*N); // 0으로 배열 초기화 for security.
	}


	// 2. 핵심 알고리즘 동작부
	while (squared > 0)
	{
		for (int i = 0; i < copy; i++)
		{
			row = row + dir;
			arr[row][col] = squared;
			if (squared == want)
			{
				x = row + 1;
				y = col + 1;
			}
			squared = squared - 1;
		}

		copy = copy - 1;
		for (int i = 0; i < copy; i++)
		{
			col = col + dir;
			arr[row][col] = squared;
			if (squared == want)
			{
				x = row + 1;
				y = col + 1;
			}
			squared = squared - 1;
		}
		dir = dir * (-1);
	}

	// 3. 결과 출력부
	for (int i = 0; i < N * N; i++)
	{
		int r = i / N;
		int c = i % N;
		cout << arr[r][c] << " ";
		if ((i % N) == N - 1) cout << endl;
	}

	cout << x << " " << y << endl;


	// 4. 2차원 배열 할당 해제부
	for (int i = 0; i < N; i++)
		delete[] arr[i];
	delete[] arr;

	return 0;
}

코드는 크게 4개의 부로 구성된다.

1. 변수 선언부

알고리즘 작성 이전에 필요로 하는 변수를 선언한 부분이다.

2. 핵심 알고리즘 동작부

배열에 값을 넣기 위한 핵심적인 알고리즘이 동작하는 부분이다.

3. 결과 출력부

$N^2$부터 1까지 달팽이 모양으로 출력하는 부분이다.

4. 2차원 배열 할당 해제부

달팽이 모양으로 값을 담기 위해 생성했던 2차원 동적 배열을 할당 해제하는 부분이다.

참고로 memset 함수는 0, -1로만 초기화 가능하다. 그 이유는 바이트 단위로 초기화가 이루어지기 때문이다.

정답 비율 & 제출 결과

초반에 알고리즘 풀지 못했을 때 정답 비율이 50%나 된다는 것에 가벼운 충격을 받았다. 최소한 둘에 하나는 풀 수 있다는 생각에 말이다. 아무튼 동시에 초심자로서 알고리즘적 사고를 잘 하는 사람들이 많다는 것에 내게 자극을 심어준 문제였다.

Reference

[1] https://walewalu.tistory.com/4

1. 문제 정의

100개의 계단이 있으며 나는 한 번에 10개의 계단을 오를 수 있는 능력을 가지고 있다.

이 때, 100개의 계단을 올라갈 수 있는 경우의 수는 몇 개인가?

2. 해결 코드

문제를 보고 생각할 수 있는 가장 초기의 코드를 작성한 것이다.

stairs = 100
skill = 10
table = [0 for i in range(stairs+1)]
table[0] = 1

for i in range(1, stairs+1):
    s=0
    for j in range(1,skill+1):
        if i-j<0:
            t=0
        else:
            t= table[i-j]
        s = s+t
    table[i] = s
print (table[stairs])

2. 초기 코드를 확인 후 줄일 수 있는 부분을 확인 후, 파이썬의 강점을 살려 개선 코드를 작성한 것이다

stairs = 100
skill = 10
table = [0 for i in range(stairs+1)]
table[0] = 1

for i in range(1, stairs+1):
    s=0
    for j in range(1,skill+1):
        t=(table[i-j],0)[i-j<0]
        s = s+t
    table[i] = s
print (table[stairs])

3. 개선 코드를 작성 후 하나의 함수로 만듦으로써 n 계단 오르기를 구현한 것이다.

def climbing(staris, skill):
    table = [0 for i in range(stairs + 1)]
    table[0] = 1
    for i in range(1, stairs+1):
        s=0
        for j in range(1,skill+1):
            t=(table[i-j],0)[i-j<0]
            s = s+t
        table[i] = s
    return table[stairs]
r =  (climbing(100,10))
print (r)

4. 함수의 최적화와 코드의 최적화를 구현한 것이며 아래의 코드는 계단 오르기 문제에 있어 가장 최적화 된 코드이다.

def climbing(n,m):
    table=[0 for i in range(n+1)]
    table[0]=1
    for i in range(1,n+1):
        s=(i-m,0)[(i-m)<0]
        table[i]=sum(table[s:i])
    return table[n]
a=climbing(100,10)
print (a)

정의

유클리드 호제법이란 두 정수 사이에 최대공약수(GCD)를 보다 효과적으로 구하는 것으로, 인류 최초의 알고리즘이라 한다. 

두 개 자연수 $A, B$가 있고 $A\ \%\ B = r$이면 다음과 같다. (단, $A > B$)

$GCD(A,B) = GCD(B,r)$

이 때, $A\ \%\ B = r$에 의해 다음과 같은 식이 기본적으로 유도된다.

$A = Bq + r$

증명

두 자연수 $A,B (A > B)$의 최대공약수를 $G$라 하자. $G$는 공약수이므로 두 서로소 $a, b$에 대해 다음 식이 성립한다.

$A = aG, B = bG$

위의 식을 사용하여 $A = Bq + r$에 대입하면 다음과 같다.

$aG = bGq + r$

$r = aG - bGq$

$ r = (a - bq)G$

$A = aG, B = bG$에서 $a, b$가 서로소라면 $G$가 최대공약수이기 때문에 $b, a - bq$가 서로소임을 증명하면 된다.

이를 증명하기 위해서는 가정에 모순을 확인하는 귀류법을 사용하여 해결할 수 있다.

$b$와 $a - bq$가 서로소가 아니라면 두 수는 공약수 $k$를 가지기 때문에 다음과 같이 나타낼 수 있다.

$a - bq = mk$

$b = nk$

위 식의 항을 옮기고 대입하여 정리하는 과정은 다음과 같다.

$a = mk + bq$

$a = mk + nkq$

$a = (m+nq)k$

따라서 다음과 같은 식을 확인할 수 있다.

$a = (m+nq)k$

$b = nk$

하지만 $a$와 $b$는 서로소이나 공약수 $k$를 가지므로 거짓 명제이다.

따라서 $a-bq$와 $b$는 서로소이다.

Reference

[1] https://baeharam.github.io/posts/algorithm/extended-euclidean/

1. 시간 복잡도

1.1 분석 종류

• $T(n)$: Every-case analysis
  • 입력크기(input size)에만 종속
  • 입력값과는 무관하게 결과값은 항상 일정

• $W(n)$: Worst-case analysis
  • 입력크기와 입력값 모두에 종속
  • 단위연산이 수행되는 횟수가 최대인 경우 선택

• $A(n)$: Average-case analysis
  
  • 입력크기와 입력값 모두에 종속
  • 모든 입력에 대해 단위연산이 수행되는 기대치(평균)
  • 각 입력에 대해서 확률 할당 가능

• $B(n)$: Best-case analysis
  
  • 입력크기와 입력값 모두에 종속
  • 단위연산이 수행되는 횟수가 최소인 경우 선택

1.2 시간 복잡도 정의

• Big-O

모든 $n$, $n \geq n_0$에 대해 $f(n) \le c\times g(n)$인 조건을 만족시키는 두 양의 상수 $c$와 $n_0$가 존재하기만 하면 $f(n)=O(g(n))$이다.

예를 들면 $O(n)$: 최악의 경우 $n$번까지 수행되면 프로그램을 끝낼 수 있다.

• Big-Omega

모든 $n$, $n \geq n_0$에 대해 $f(n) \geq c\times g(n)$인 조건을 만족시키는 두 양의 상수 $c$와 $n_0$가 존재하기만 하면 $f(n)=\Omega(g(n))$이다.

예를 들면 $O(n)$: 최소 $n$번은 수행되어야 프로그램을 끝낼 수 있다.

• Theta

모든 $n$, $n \geq n_0$에 대해 $c_1\times g(n) \le f(n) \le c_2\times g(n)$인 조건을 만족시키는 세 양의 상수 $c_1, c_2, n_0$가 존재하기만 하면 $f(n)=\theta(g(n))$이다.

Theta의 경우 $O와\ \Omega$의 교집합이다. 즉, 차수가 같은 문제이다.

• Small-O

모든 $n$, $n \geq n_0$에 대해 $0 \leq f(n) \lt c \times g(n)$인 조건을 만족시키는 두 양의 상수 $c, n_0$가 존재하기만 하면 $f(n)=O(g(n))$이다.

예를 들면 $O(n)$: 최악의 경우에도 n번 미만으로 수행되면 프로그램은 끝낼 수 있다.

$\lim_{x \to \infty}$ $f(x)\over g(x)$ $=0$로 나타낼 수 있다.

Small-O와 Big-O의 차이점은 다음과 같다.

- Big-O는 실수 $c>0$ 중에서 하나만 성립해도 된다.

- Small-O는 모든 실수 $c>0$에 대해서 성립해야 한다.

- Small-O는 Big-O에서 등호를 뺀다.

추가적으로 Small-omega($\omega$)도 존재한다.

1.3 시간복잡도 정의를 이용하여 다음 4개의 문제에 대하 statement의 참, 거짓을 판별하시오 (시간복잡도 계산 문제)

1.4 $8n^2 + \sqrt2 = O(n^2)$임을 보여라.

모든 $n, n \geq n_0$에 대하여 $f(n) \leq c \times g(n)$인 조건을 만족시키는 두 양의 상수 $c$와 $n_0$가 존재하기만하면 $f(n) = O(g(n))$이다.

1. $f(n) = 8n^2 + \sqrt2$

2. $g(n) = n^2$

3. 대입 => $8n^2 + \sqrt2 \leq c \times n^2$

4. $\sqrt2$는 약 1.414

5. $8n^2 + 1.414 \leq c \times n^2$

6. n = 2라 가정하면

7. $32 + 1.414 \leq c \times 4$

8. $33.414 \leq c \times 4$

9. $c \geq 9$

1.5 Big-O, Omega, Theta, small-o의 정의를 이용하여 $5x^3 + 4x^2 + 6x \in \Theta(n^3)$ 임을 보이시오.

1. $g(x) = x^3$

2. $g_2(x) = 6x^3$

3. $x^3 \leq 5x^3+4x^2+6x \leq 6x^3$

2. 프림, 크루스칼, 다익스트라

2.1 비방향 그래프를 보고 크루스칼 알고리즘을 이용하여 최소 비용 신장 트리를 구하는 과정을 단계별로 보이시오

• 크루스칼 알고리즘의 핵심
  • 오름차순
    1. 가중치를 기준으로 간선을 오름차순 정렬
    2. 낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가
    3. 사이클을 형성하는 간선을 추가하지 않음
    4. 간선의 수가 정점의 수보다 하나 적을 때 MST가 완성
  • 내림차순
    1. 가중치를 기준으로 간선을 내림차순으로 정렬
    2. 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거
    3. 두 정점을 연결하는 다른 경로가 없을 경우 해당 간선은 제거하지 않음
    4. 간선의 수가 정점의 수보다 하나 적을 때 MST가 완성

2.2 그래프를 보고 다익스트라 알고리즘을 이용하여 v6를 출발점으로하는 최단 거리를 구하는 과정을 단계별로 보이시오

• 간선의 가중치를 오름차순으로 정렬한다.
• 가중치가 낮은 순서대로 간선을 하나씩 그래프에 추가한다.
• 그래프 내에서 사이클을 형성하는 간선은 추가하지 않는다.
• 간선의 개수가 정점의 개수보다 '1' 작으면 끝낸다.

3. NP, NP-complete

3.1 NP, NP-hard, NP-complete의 정의

• $P$ : 어떤 문제가 주어졌을 때 다항식으로 표현되어 polynomical time 즉, 다항 시간내에 해결 가능한 알고리즘을 의미하며 알고리즘의 복잡도가 $O(n^k)$로 표현되는 문제를 '$P$'라 한다. (복잡도 $O(n^k)$ 이하를 가지는 경우 같은 복잡도 내에 모든 해를 구한다.)

• $NP$ : 어떤 문제가 주어졌을 때 다항식으로 표현될 수 있는지의 여부가 결정되지 않은 문제들을 'NP(Non-deterministic polynomial)'라 한다.

• $NP-Complete$ : NP이면서 동시에 NP-Hard 에 속한다면 그 문제는 'NP-Complete'라 한다. (전수조사가 답)

• $NP-Hard$ : 적어도 모든 NP 문제만큼은 어려운 문제들의 집합이며, 만약 P-NP 문제가 P=NP로 풀린다면 P=NP=NP-Complete이므로 P와 NP는 NP-Hard의 부분집합이 되고, P≠NP인 경우는 P와 NP-Hard는 서로소가 된다. *다항시간 : $T(n) = O(n^k), k$ 는 상수  => $k$가 상수로 고정이 된다면 그 문제는 해결하기 쉬운 문제. 다항시간안에 풀 수 있는 문제이므로.

3.2 해밀턴회로 거리 구하기(그래프가 주어질 때 그래프의 모든 점을 정확하게 한번씩만 지나는 경로가 존재하는가?) (NP-hard)

4. 배열 제시 후 소팅 알고리즘을 사용하여 정렬 과정을 보여라

4.1 Merge sort 알고리즘을 사용하여 8개의 숫자를 정렬하는 과정을 보여라

4.2 각종 정렬 기법들의 장단점과 시간복잡도

5. Divide and Conquer 알고리즘과 Dynamic Programming 알고리즘 차이

5.1 분할 정복법이 비효율적인 경우를 설명하라

5.2 분할 정복법과 동적프로그래밍을 이용하여 이항계수를 구하는 알고리즘 작성 후 두방식의 차이점에 대해 적으시오

• 분할 정복법(Divide and Conquer)
  • 어떠한 큰 문제를 해결하기 위해 큰 문제를 작은 단위의 문제로 나누어 해결하는 방법 (Top-down)
  • 문제의 크기가 충분히 작아질때까지 반복적으로 분할
  • 해결한 작은 문제를 가지고 바로 윗 단계의 문제를 해결해 나가는 방식
  • 대표적인 예로는 Binary Search와 Merge Sort, Quick Sort 등이 있다.

• 동적 프로그래밍(Dynamic Programming)
  • 문제를 작은 인스턴스들로 나누고 Bottom-up 순서로 풀어나가면서 문제의 값을 정해놓고 필요할 때 가져와  문제를 해결하는 방식이다. "기억하며 풀기"라 생각하면 된다.
  • 대표적인 예로는 TSP 문제, 피보나치 수열, 파스칼의 트리 작성 등이 있다.

분할정복법과 동적 프로그래밍의 공통점과 차이점

• 공통점 : 문제를 작은 단위로 나누어 해결
• 차이점 : 분할정복법은 Top-down 방식이며, 동적 프로그래밍은 Bottom-up 방식이다.

5.3 Binomial coefficient를 계산하려할 때 다음을 구해라

• Divide-and-Conquer 방법을 사용하는 pseudo code 작성
• Dynamic Programming 방법을 사용하는 pseudo code 작성
• 위 두 접근 방법의 차이점을 서술

5.4 이항계수 수학적 귀납법으로 증명하고, 동적 프로그래밍으로 알고리즘을 구현하라.

bottom-up 방식

int binomial(int n, int k) 
{
 for (int i=0; i<=n; i++) 
 {
     for (int j=0; j<=k && j<=i; j++) 
     {
         if (k==0 || n==k)
             arr[i][j] = 1;
         else
             arr[i][j] = arr[i-1][j-1] + arr[i-1][j];
     }
 }
 return arr[n][k];
}

6. DFS(Depth First Search)와  BFS(Breadth First Search)의 차이

• DFS, BFS의 의사코드를 작성하고 이들의 차이를 제시한 다음, 간단한 트리를 작성하여 순회하는 것을 보이시오.

8. 행렬을 주고 TSP에 관한 문제

9. Strassen 행렬 알고리즘을 사용하여 2*2 행렬 A,B의 곱 C를 구하라(m1,m2,...,m7)을 사용해야함

9.1 Strassen's Matrix Multiplication 알고리즘에 대해 설명하라

9.2 행렬 곱셉 알고리즘 + 쉬트라센 + 복잡도

아래와 같이 행렬 A,B가 있고 두 행렬의 곱이 행렬 C로 표현한다 가정한다.

$A = \left[ \begin{array}{cc|c} a_{11} & a_{12} \\\\ a_{21} & a_{22} \end{array} \right],\ $ $B= \left[ \begin{array}{cc|c} b_{11} & b_{12} \\\\ b_{21} & b_{22} \end{array} \right],\ $ $C=\left[ \begin{array}{cc|c} c_{11} & c_{12} \\\\ c_{21} & c_{22} \end{array} \right]$

이 때, $A_{ij},B_{ij},C_{ij} \in F^{2^n-1 \times 2^n-1}$ 이다.

따라서 일반적인 행렬의 곱은 다음과 같이 표현할 수 있으며, 총 8번의 곱셈과 4번의 덧셈으로 연산된다.

$C_{11} = A_{11}B_{11} + A_{12}B_{21}$ 
$C_{12} = A_{11}B_{12} + A_{12}B_{22}$ 
$C_{21} = A_{21}B_{11} + A_{22}B_{21}$ 
$C_{22} = A_{21}B_{12} + A_{22}B_{22}$

슈트라센 알고리즘은 행렬의 곱셉을 더하기 연산으로 풀어 각 원소를 구할 수 있는 $M$이라는 연산 행렬로 표현한다. 행렬 $M$은 7번의 곱셈과 10번의 덧셈으로 연산으로 나타낼 수 있으며 아래와 같이 표현한다.

$M_1 = (A_{11} + A_{22})(B_{11}+B_{22})$ 
$M_2 = (A_{21} + A_{22})B_{11}$ 
$M_3 = A_{11} (B_{12}-B_{22})$ 
$M_4 = A_{22}(B_{21}-B_{11})$ 
$M_5 = (A_{11} + A_{12})B_{22}$ 
$M_6 = (A_{21} - A_{11})(B_{11}+B_{12})$ 
$M_7 = (A_{12} - A_{22})(B_{21}+B_{22})$

최종적으로 행렬 C는 행렬 M의 더하기 연산으로 이루어져 있으며 각 원소에 해당하는 방법은 다음과 같다.

$C_{11} = M_1 + M_4 - M_5 + M_7$ 
$C_{12} = M_3 + M_5$ 
$C_{21} = M_2 + M_4$ 
$C_{22} = M_1 - M_2 + M_3 + M_6$

10. 5-Queen 문제를 백트래킹과 상태 설명 트리를 사용하여 해결하라

11. Floyd 알고리즘을 사용하여 W(=D0) 행렬과  D(=D) 행렬을 구하라. W, D를 구하는 과정을 서술하라

11.1 방향 그래프를 보고 플로이드 알고리즘을 이용하여 D와  P를 단계별로 적으시오.

12. 하노이의 탑 알고리즘을 써라

#include <stdio.h>

void HanoiTowerMove(int num, char from, char by, char to)
{
	if (num == 1)
		printf("원반 1을 %c에서 %c로 이동 \n", from, to);
	
	else
	{
		HanoiTowerMove(num - 1, from, to, by);
		printf("원반 %d를 %c에서 %c로 이동 \n", num, from, to);
		HanoiTowerMove(num - 1, by, from, to);
	}
}

int main(void)
{
	// 막대 A의 원반 5개를 막대 B를 경유하여 막대 C로 옮기기
	HanoiTowerMove(5, 'A', 'B', 'C');
	return 0;
}

13. 탐욕적 방법 Greedy Algorithm이 항상 최적의 해를 내지 못하는 경우의 예를 들라

Greedy Algorithm이 사용되는 대표적인 예제로는 "최소 수의 동전으로 거스름돈 거슬러주기" 문제가 있다. 

만약 우리가 마트의 캐셔로 일을 하고 있고, 850원을 거슬러 주어야 할 때 500원 동전 1개와 100원 동전 3개와 50원 동전 1개 총 4개의 동전을 건넴으로써 최소한의 동전을 거슬러 줄 수 있다. 하지만 이렇게 하지 않고 10원짜리 동전 85개를 건네주거나 50원짜리 17개를 건네주는 방법과 같이 다양한 경우의 수가 존재하며 이와 같을 경우 반드시 최적의 해를 내는 것은 아니다.

또한 우리나라의 경우 총 4개의 동전 500원, 100원, 50원, 10원이 있다. 하지만 만약 400원 동전이 발행된다면 400원 동전 2개, 50원 동전 1개를 통해 총 3개의 동전을 거슬러 줄 수 있을 것이다. 가장 최적의 방법이지만, 기존 알고리즘에 따르면 500원 1개, 100원 3개, 50원 1개로 거슬러주게 될 것이다. 이와 같이 탐욕 알고리즘은 항상 최적의 결과를 보장하지 못한다. 

Reference

[1] https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

[2] https://janghw.tistory.com/entry/알고리즘-Greedy-Algorithm-탐욕-알고리즘