For a better world

About SSH

AWS나 GCP와 같은 클라우드 플랫폼을 사용하다보면 주로 SSH를 통해 접속하고 작업을 진행하게 된다. SSH 사용에 대한 이해는 암호학에서 나오는 공개키와 비밀키의 관계를 이해하는 것이 핵심이다. 본 포스팅에서는 Windows 10과 Windows Server 2016간의 예시를 통해 이러한 SSH의 공개키와 비밀키가 어떻게 사용되는지를 설명하고자한다.

SSH 설치

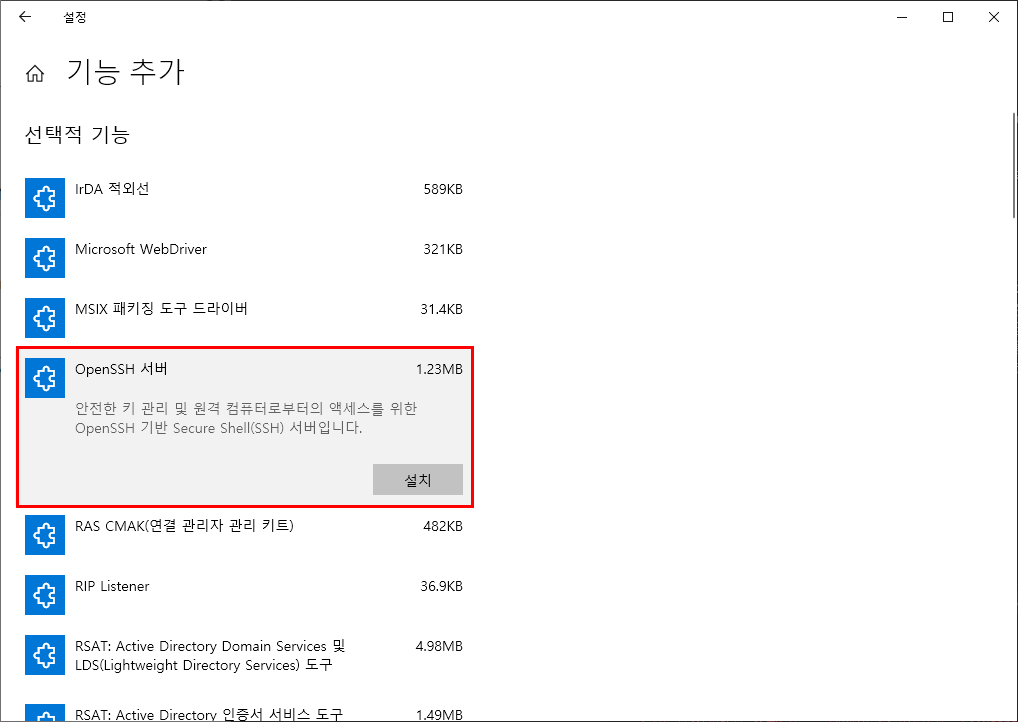
Windows Server 2016의 경우 Windows 10과 달리 기본적으로 내장되어 있는 ssh가 없어서 별도의 OpenSSH와 같은 어플리케이션을 설치해주어야 한다. Winodws 10의 경우에도 빌드 버전에 따라 내장된 ssh가 없을 수 있으나 만약 없을 경우 설정 > 앱 > 선택적 기능 > 기능 추가 > OpenSSH 서버를 선택하여 설치하면 된다. OpenSSH에 대한 설치 과정과 환경 설정은 본 포스팅에서는 언급하지 않는다.

키 생성

Windows 10 : Client
Windows Server 2016 : Server

만약 Local인 Windows 10에서 Remote인 Windows Server 2016에 SSH를 접속하고 싶을 경우 접속을 위해 키 페어를 생성해야한다.

키 페어를 생성하여 SSH 통신을 하기 위해서는 실제로 작업을 진행하는 Local에서 공개키/비밀키 쌍을 생성하여 공개키를 Remote에 두어야 한다.

키 페어를 생성하기 위해 아래와 같이 ssh-keygen -t rsa 명령을 사용하면 어떠한 이름의 키 페어를 생성할 것인지를 확인하며 입력 없이 Enter를 누르게되면 default 이름인 id_rsa로 설정된다. (-t 옵션은 type을 의미하고 추가적으로 -C 옵션은 comment, -b 옵션은 bit 수를 지정이 가능. default bit수는 2048임)

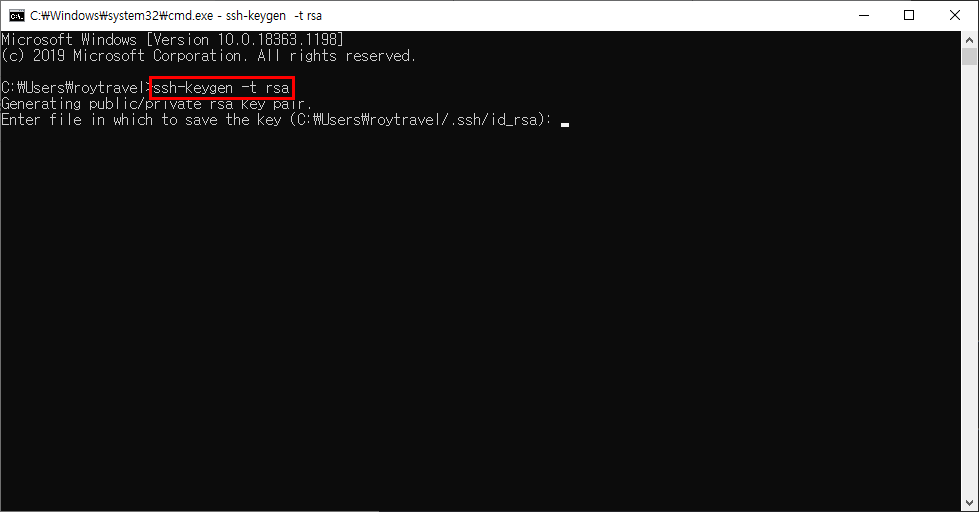
이후 비밀키를 특정 passphrase로 암호화 할 것인지에 대해 확인하며 입력 없이 Enter를 누르게 되면 키 페어가 생성된다.

생성된 키 페어는 사용자 폴더 하위의 .ssh 폴더에 생성되며 아래와 같이 비밀키인 id_rsa와 공개키인 id_rsa.pub이 생성된다.

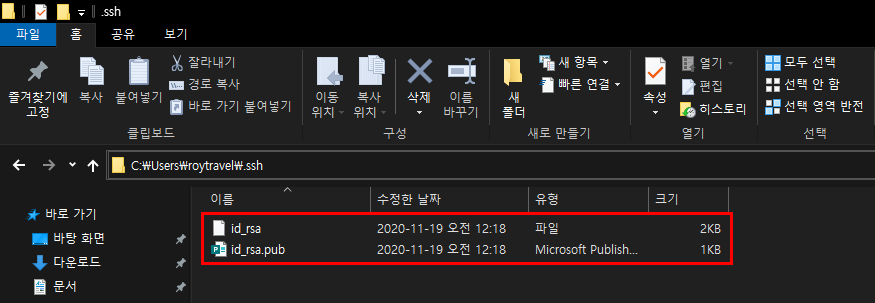
생성된 키 페어 중 공개키인 id_rsa.pub을 remote로 작업할 Windows Server 2016의 .ssh 폴더 하위에 아래와 같이 authorized_keys에 추가해주어야 한다.

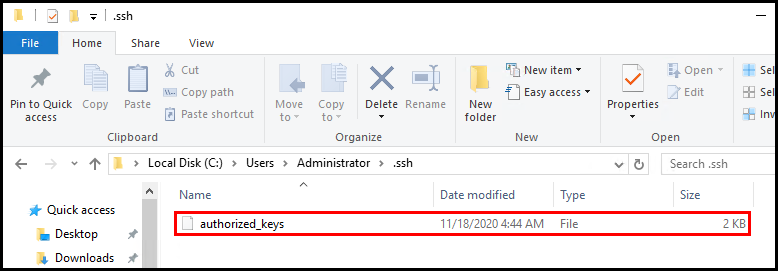
authorized_keys가 없을 경우 파일을 생성하고 id_rsa.pub의 데이터를 동일하게 복붙해주면 된다.

SSH 사용

SSH를 사용하기 위해서는 3가지 파일이 필요하다.
Local : id_rsa, config
Remote : authorized_keys

이 중 id_rsa와 authorized_keys의 경우 키 페어 생성을 통해 얻을 수 있는 파일이며, 마지막으로 config 파일이 필요한데 별도로 존재하지 않을 경우 아래와 같이 작성해주어야 한다.

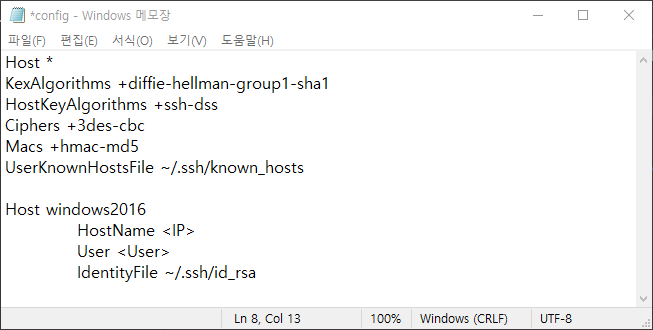
Host 명의 경우 추후 ssh 명령을 사용할 때 축약하여 사용할 수 있는 것으로 임의 설정이 가능하다. HostName의 경우 접속하고자 하는 remote의 IP이며, User의 경우 remote 환경의 사용자 계정 이름을 의미한다. 여기서는 Windows Server 2016의 사용자 계정인 Administrator라 볼 수 있다.

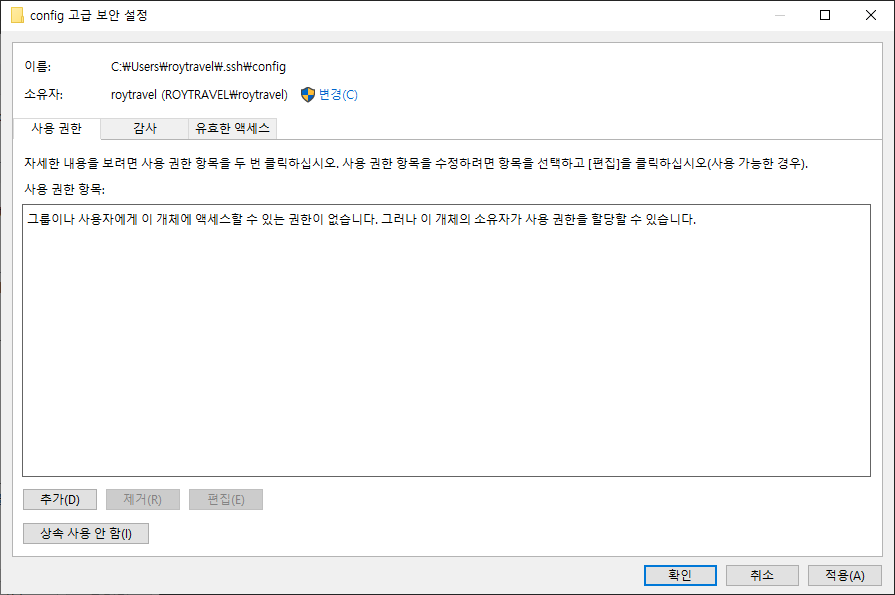
이후 중요한 것은 config 파일의 사용 권한 설정이다. 일반적으로는 아래와 같이 3개의 보안 주체가 있는 것을 확인할 수 있을 것이다.

여기에서 모든 보안 주체에 대해 상속을 사용하지 않음을 설정해주고 아래와 같이 모두 제거를 진행하여야 한다.

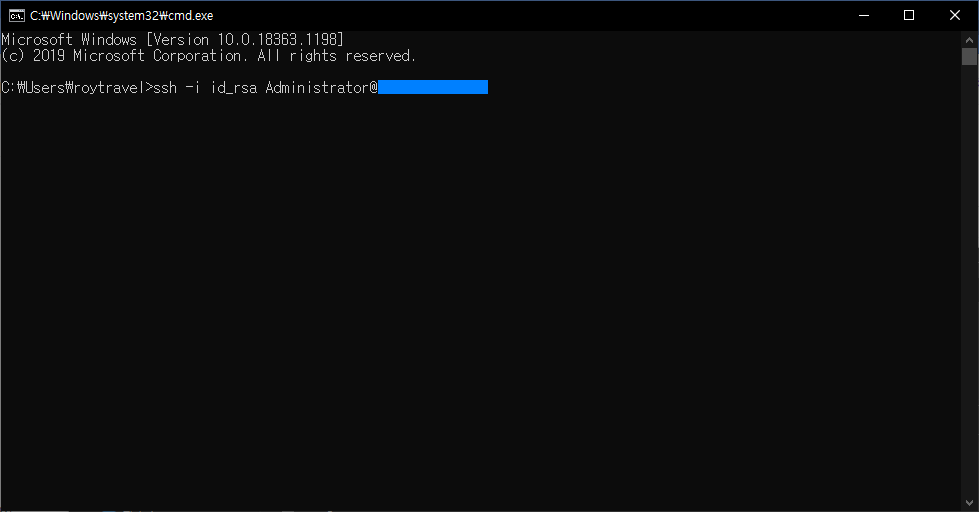
이후 아래와 같이 ssh [User]@[IP]와 같은 명령어를 작성할 경우 비밀번호 입력창이 뜨는 것을 확인할 수 있다.

이후 remote로 접속하는 비밀번호를 입력해주면 아래와 같이 접속이 완료된 것을 확인할 수 있다.

만약 비밀번호 없이 바로 접속하고 싶다면 아래와 같이 -i 옵션을 통해 비밀키인 id_rsa를 입력해주면 비밀번호 없이 remote로 접속이 가능하다.

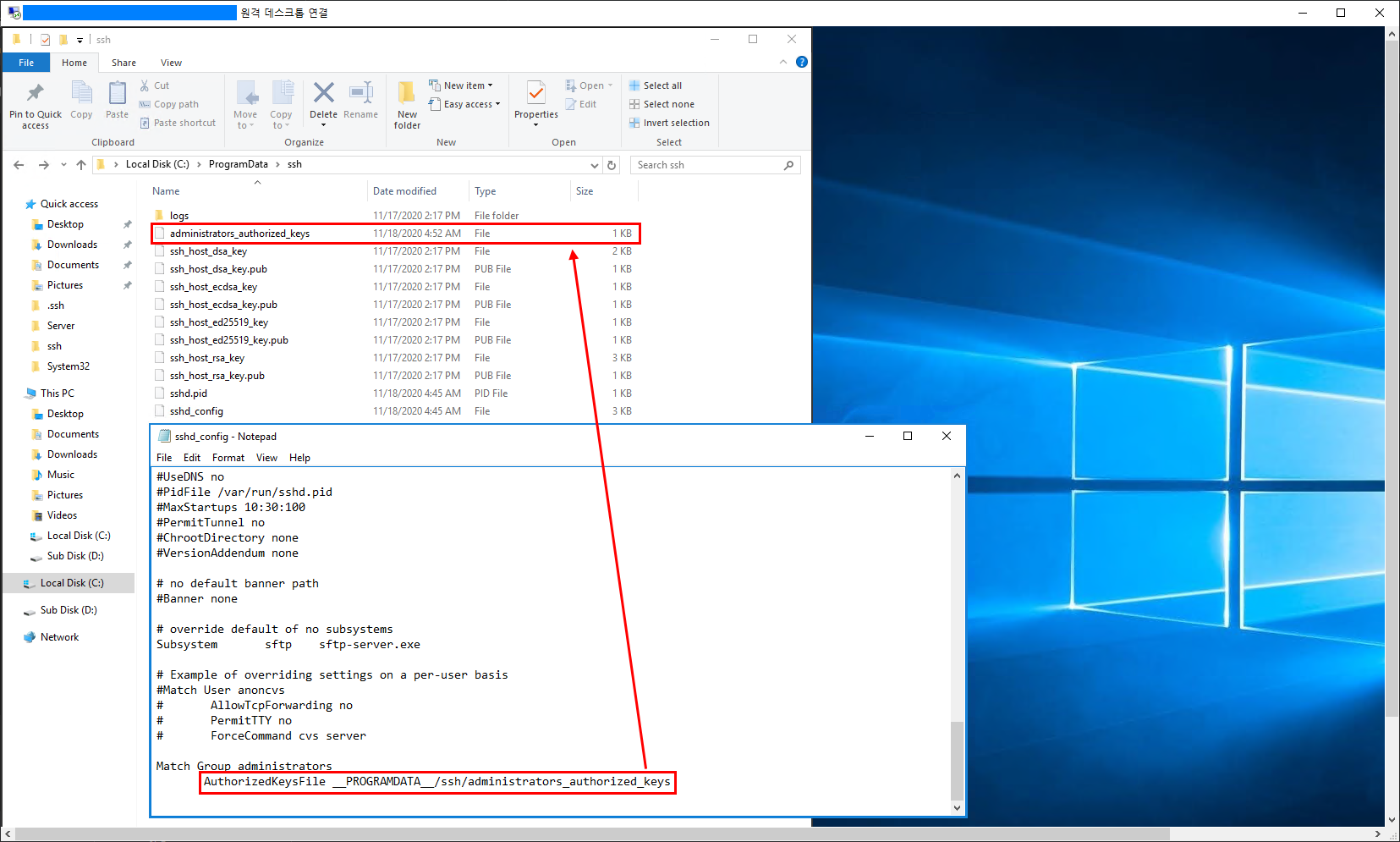
다만 비밀번호 없이 바로 접속하기 위해서는 remote 측에서도 아래와 같이 OpenSSH가 설치된 C:\ProgramData\SSH의 폴더에서 authorized_keys 파일을 추가해주어야 비밀번호 없이 client에서 -i 옵션을 사용하여 접속이 가능하며, authorized_keys 파일은 sshd_config 파일의 맨 아래에서 경로를 설정해줄 수 있다.

만약 remote에 있는 파일을 실행하고 싶을 경우 아래와 같은 명령을 통해 파이썬 파일을 실행할 수 있다.

또한 scp 명령을 통해 remote와 local간의 데이터를 주고 받을 수 있는데 remote로부터 local로 데이터를 가져오는 명령은 다음과 같다.

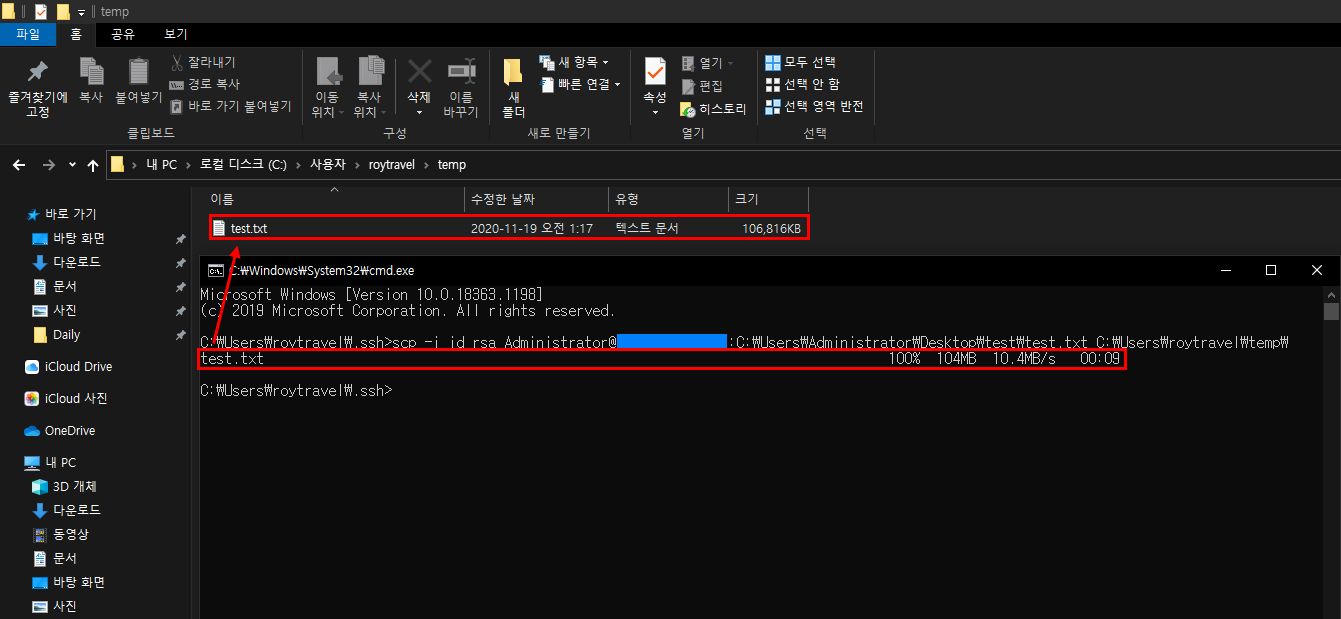
아래와 같이 파이썬 스크립트를 통해서도 SSH 통신으로 명령을 내리고 결과를 받아오는 것이 가능하다.

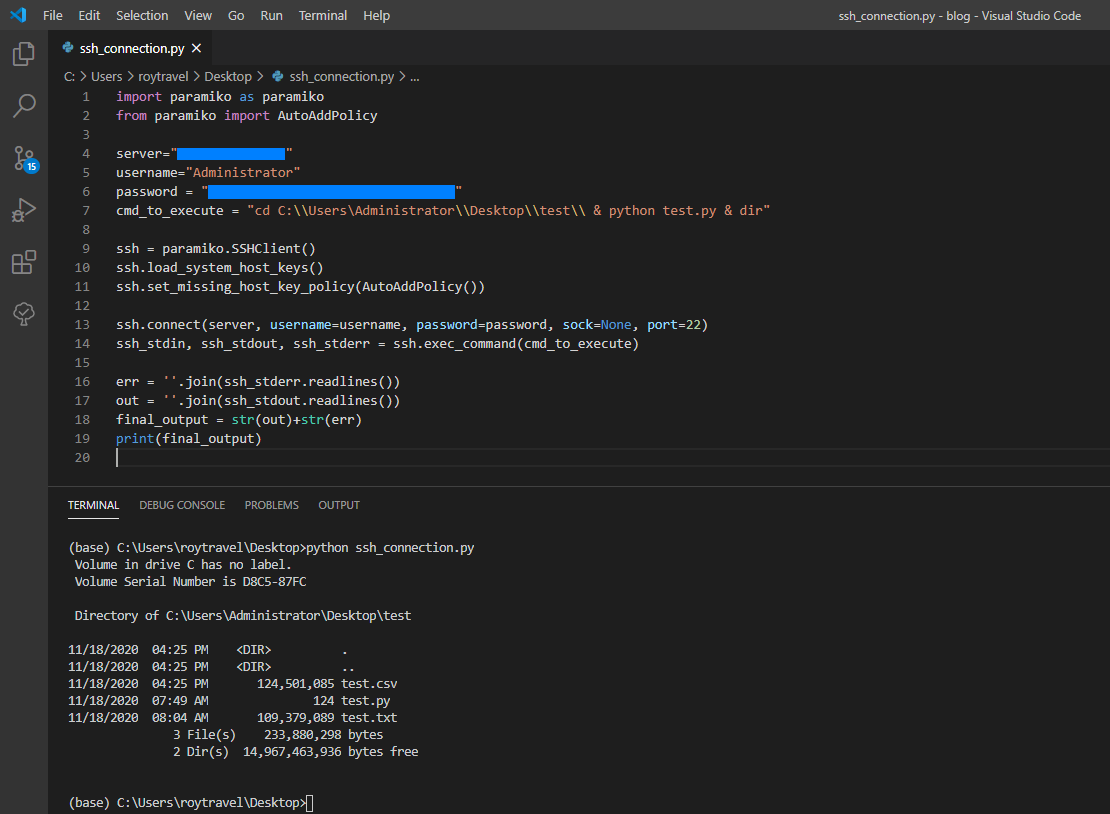
사용한 파이썬 코드는 다음과 같다.

# -*- coding:utf-8 -*-
import paramiko as paramiko
from paramiko import AutoAddPolicy

server=""
username="Administrator"
password = ""
cmd_to_execute = "cd C:\\Users\Administrator\\Desktop\\test\\ & python test.py & dir"

ssh = paramiko.SSHClient()
ssh.load_system_host_keys()
ssh.set_missing_host_key_policy(AutoAddPolicy())

ssh.connect(server, username=username, password=password, sock=None, port=22)
ssh_stdin, ssh_stdout, ssh_stderr = ssh.exec_command(cmd_to_execute)

err = ''.join(ssh_stderr.readlines())
out = ''.join(ssh_stdout.readlines())
final_output = str(out)+str(err)
print(final_output)

Reference

[1] How to Use SSH in Windows: 5 Easy Ways

소프트웨어 개발 주기는 요구사항 분석, 설계, 구현, 배포, 유지보수 등과 같은 일련의 과정이 존재한다. 이러한 소프트웨어 개발에 있어 사용하는 방법은 크게 두 가지를 사용한다.

1. 폭포수 모델

(개념) 요구사항을 완벽하게 취합하여 계획을 잘 세우고 그 계획대로 진행하는 방법론

(배경) 1970년대 창안된 첫 번째 소프트웨어 개발 방법론

(아키텍처) 요구사항 → 분석 → 디자인 → 코딩 → 테스트 → 릴리즈 단계를 지님

(특징) 미리 모든 요구사항을 수집하고 전체적으로 분석과 디자인을 한 뒤 한번에 완성

(단점-1) 느린 단계별 접근법으로, 중복 프로세스가 발생하고 릴리즈 간 긴 시간차가 발생

(단점-2) 과도한 문서 업무가 존재함

(보완 방안) 애자일 방법론을 고안

1. 애자일 방법론

(개념) 요구사항을 초기에 완벽하게 도출하는 것이 불가능하기에 개발 주기를 반복하고 고객과 소통하면서 소프트웨어의 품질을 발전시키는 방법론

(전제) 모든 요구사항을 결코 알 수 없다.

(배경) 폭포수 모델의 과도한 문서업무로 인해 비효율을 줄이고자 1990년대 고안된 방법론

(특징) 빠르고 모듈식의 주기적인 방식을 통해 개발 전 단계에 걸쳐 요구사항을 지속적으로 분석하고 반영하여 릴리즈 간 시간차를 최소화함

3. 폭포수와 애자일 방법론의 10가지 주요 차이점

• 요구사항 : 폭포수 = 미리 도출 / 애자일 = 지속적으로 도출
• 릴리즈 : 폭포수 = 자주하지 않음 / 애자일 = 고객 니즈 충족을 목표로 지속적으로 릴리즈
• 지향 : 폭포수 = 계획 중심 / 애자일 = 학습 중심
• 의사소통 : 폭포수 = 고객과의 드문 의사소통 / 애자일 = 고객과의 지속적인 의사소통
• 현황 공유 : 폭포수 = 계획중심이라, 단계별 진척 사항을 프로젝트 단계별 점검 / 애자일 = 특정 기능이 완성되지 않은 소프트웨어더라도 프로젝트 초기부터 전체적으로 통합되기까지 지속적으로 진행사항 공유
• 수직/수평 : 폭포수 = 수평적 단계별 개발 / 애자일 = 기능별 수직 개발
• 관점 : 폭포수 = 프로그래밍은 단순 공사 / 애자일 = 프로그래밍은 디자인의 확장(분리불가)
• 통합 : 폭포수 = 마지막에 통합 / 애자일 = 초기와 이후 지속적인 통합
• 테스트 : 폭포수 = 마지막 단계에 테스트 / 애자일 = 초기와 이후 지속적인 테스트
• 진단방법 : 폭포수 = 계획에 따른 진척사항 진단 / 애자일 = 소프트웨어를 만들지 소프트웨어 만드는 방법을 문서화하는 것이 아니기에 소프트웨어가 얼마나 회사 비즈니스에 부합하나로 진단

4. Reference

• https://blog.naver.com/PostView.nhn?blogId=selrim11&logNo=50173044263 (폭포수, 애자일)

디피헬만 키 교환 프로토콜의 경우 간단한 형태이다. 예시를 들자면 A, B가 있을 때 A는 B에게 3을 보내고 B는 6에게 보냈다고 할 경우 서로 3과 6을 곱한 값인 18을 세션키로 사용하는 것과 같다.

세션키를 만들기 위해 각자의 개인키를 g의 승수로 취해 모듈러 연산을 한 다음 보낸다. Bob는 세션키를 생성하기 위해 Alice로부터 받은 $R_1$에 자신의 개인키인 $y$를 곱해주고,  Alice는 세션키를 생성하기 위해 해 Bob으로부터 받은 $R_2$에 자신의 개인키인 $x$를 곱하여 같은 세션키를 사용한다.

블록체인에서도 주로 언급되는 영지식 증명의 경우 아래 3가지 조건을 충족시켜야 한다.

Completeness(완전성): 어떤 문장이 참이면 정직한 증명자는 정직한 검증자에게 이 사실을 납득시킬 수 있어야 한다.

Soundness(건전성): 어떤 문장이 거짓이면 부정직한 증명자는 정직한 검증자에게 이 문장이 사실이라고 납득시킬 수 없어야 한다.

zero-knowledgeness(영지식성): 어떤 문장이 참이면, 검증자는 문장의 참거짓 이외에는 아무것도 알 수 없어야 한다.

암호학적으로 해시를 안전하게 설계하기 위해서는 크게 3가지 조건이 필요하다.

이를 해시의 3가지 성질이라 한다.

제 1역상 저항성(pre-image resistance)

• 주어진 output 값으로 원래의 input을 알아내기 어려워야 한다.
• 주어진 해시값 y로부터 $h(x)=y$를 만족하는 x를 찾는 것이 어려워야 함을 의미한다.

제 2역상 저항성(second pre-image resistance)

• 동일한 output을 가지는 input이외의 input'을 찾기 어려워야 한다.
• 해시함수 h와 x값이 주어졌을 때 동일한 y값을 내는 x`을 찾기 어려워야 한다.

충돌 저항성(collision resistance)

• 서로 다른 입력 값을 해시했을 때 같은 output이 나오기 어려워야 한다.
• 해시함수 h가 주어졌을 때 동일한 y값을 내는 $(x, x')$ 쌍을 찾기 어려워야 한다.

한마디로 말해 차례대로 $x, x', (x,x')$을 찾기 어려워야 한다.

1. Elgamal 암호 알고리즘 개요

Elgamal 암호는 공개키암호시스템으로서 디피헬만의 키교환과 같은 원리를 사용하는 것이 특징이다. Elgamal 암호는 이산대수 문제의 어려움에 기반하고 있다. 예를 들어 (x,g,p)가 주어졌을 때 y=g^x mod p는 계산하기 쉽지만, (y,g,p)가 주어졌을 때 x를 찾기 쉽지 않다는 것이다. Elgamal 암호는 Textbook-RSA보다 암호문의 길이가 2배나 길다. 하지만 동일한 평문에 대해 동일 암호문을 출력하는 Textbook-RSA와 달리 동일 평문에 대해 매번 다른 암호문을 출력하는 probabilistic한 성질을 가진다.

키생성

1. 큰 소수 $p$를 선택한다.

2. $1\leq d\leq p-2$의 범위에서 임의의 d를 선택한다.

3. $Z_p^*$에서 임의의 원시근 $e_1$을 선택한다.

4. $e_2=e_1^d\ mod\ p$를 계산한다.

암호화

1. 메시지 $m$과 랜덤 $r$을 선택

2. $c_1=e_1^r\ mod\ p$를 계산

3. $c_2=e_2^rm\ mod\ p$를 계산

4. $(c1, c2)$를 수신자에게 전송

복호화

개인키 d를 이용해 $c_2(c_1^d)^{-1}\ mod\ p$를 계산 → M 도출 가능

$c_2(c_1^d)^{-1}\ mod\ p$

= $c_2e_1^{-rd}\ mod\ p$

= $e_2^rm*e_1^{-rd}\ mod\ p$

= $e_1^{rd}me_1^{-rd}\ mod\ p$

= $m\ mod\ p$

2. Elgamal 암호 알고리즘과 KPA 공격

random number를 사용하지 않으면 Elgamal 암호는 KPA 공격에 취약하다. KPA 공격은 알려진평문공격으로 공격자가 평문에 대응하는 암호문 쌍 일부를 알고 있을 때다. 공격자는 이를 통해 새로운 평문에 대해 평문과 키를 알아내는 것을 목표로 한다.

방법 1

공격자는 자신이 알고 있는 평문 m과 $(c_1,c_2)$를 이용해 아래와 같이 계산가능하다.

$c_2=e_2^rm\ mod\ p$

$e_2^r=c_2m^{-1}\ mod\ p$

이때 공격자는 자신이 원하는 $m^*$에 대해 아래와 같은 과정을 통해 알 수 있다.

$c_1^*= e_1^r\ mod\ p$

$c_2^*=e_2^rm^*\ mod\ p$

일 때 이미 계산해둔 정보를 통해 아래와 같이 계산하여 $m^*$를 얻을 수 있다.

$(e_2^r)^{-1}c_2^ = m^*\ mod\ p$

방법 2

$[m]$
1) $C_1=e_1^r\ mod\ p$

2) $C_2 = e_2^r*m\ mod\ p$

$[m']$
1) $C_1'=e_1^r\ mod\ p$

2) $C_2'=e_2^r*m'\ mod\ p$

$\therefore {C_2\over C_2`}={{e_2^rm\ mod\ p}\over {e_2^rm'\ mod\ p}}$

attacker가 m를 알고 동일한 r값이 쓰였다면 m'을 알게 되는 것과 같아지기 때문에 Elgamal은 KPA 공격에 안전하지 않다.

1. RSA 알고리즘 개요

공개키 암호에는 대표적으로 RSA 암호가 일반적으로 사용된다. 하지만 RSA 알고리즘의 경우 수학적으로 안정성이 검증되지 않았고, 취약점이 나올 경우 거기에 맞춰 알고리즘을 수정하는 방식을 사용한다고 한다. 기본적으로 RSA 알고리즘은 같은 메시지에 대해서 같은 암호문을 생성하는 결정적인 특징을 가진다. 이를 방지하고자 확률적인 특징을 가지도록 하기 위해 고정패딩과 랜덤패딩을 붙이는 RSA-OAEP 방식을 사용한다. RSA-OAEP는 RSA 알고리즘의 취약점 중 하나인 CCA(선택암호문공격)에 안전하다는 것이 특징이다. RSA 암호이외에도 레빈 암호 시스템이 있다. 이는 수학적으로 안정성이 검증되었고 RSA보다 뛰어난 것으로 판단되었지만 RSA 암호보다 유명세를 타지 못해 별로 사용되지 않는 것이라 한다.

2. RSA 알고리즘

절차

(1) 서로 다른 두 소수 $p, q$를 선택
(2) $p$와 $q$를 곱하여 $n=p*q$를 계산
(3) $\phi(n) = (p-1)(q-1)$을 계산
(4) $1<e<\phi(n)-1$의 범위에서 공개키 $e$를 선택
(5) $d=e^{-1}\ mod\ \phi(n)$을 통해 비밀키 $d$를 계산
——————————
public key = $(n, e)$
private key = $(d)$
검증키 = $(n,e)$
서명키 = $(d)$

암호화 (Encryption)

$C \equiv m^e\ mod\ n$

복호화 (Decryption)

$m \equiv C^d\ mod\ n$

서명 (Signing)

$S \equiv H(m)^d\ mod\ n$ // $H()$ is hash function

검증 (Verification)

check if $S^e \equiv H(m)\ mod\ n$

$S^e \equiv (H(m)^d)^e\equiv H(m)$

= $m$과 $s$가, 검증키 $(e,n)$을 이용하여 $s^e\ mod\ n = m$이 되는지 확인.

3. RSA 알고리즘에 대한 선택암호문공격

1. $c = m^e\ mod\ n$이 주어짐.

2. 공격자는 $gcd(r,n)=1$이면서 $r\in(0,n-1)$을 선택

3. 공격자는 공개키 r을 이용하여 암호화하여 $c^*\equiv\ r^ec\ mod\ n$을 생성

4. 복호화 오라클로 전송하여 $c^{*d}\equiv\ ({r^ec})^d\ mod\ n$을 받음

5. $c^{*d}\equiv\ rc^d\ mod\ n$

6. $c^{*d}\equiv r(m^c)^d\ mod\ n$

7. $c^{*d} \equiv\ rm\ mod\ n$

8. $c^{*d}r^{-1} \equiv m\ mod\ n$을 통해 m을 구할 수 있음. 공격자는 자신이 선택한 r에 대응하는 역원
을 곱하면 됨.

현대암호학에서 사용되는 블록 암호 운용 방식은 크게 5가지가 존재한다.

5가지를 확인하기 이전 핵심에 대한 이해를 위한 키워드는 다음과 같다.

Keyword: 개념, 암호화, 복호화, 장단점, 블록재사용, 병렬처리, 에러전파

1. ECB(Electronic Code Book)

ECB는 운용모드중 가장 간단한 형태로 암호화와 복호화가 독립적으로 이루어진다. 때문에 병렬처리가 가능하다는 장점이 있다. 반면 블록의 암호화와 복호화에 사용하는 키가 같기 때문에 같은 평문에 대해 같은 암호문이 나온다는 단점이 있다. 때문에 블록재사용과 같은 취약점이 발생할 수 있다. 암호문 생성 또는 전송 중에 에러가 발생할 수 있다. 이러한 에러에 있어서 ECB는 독립적으로 암복호화되기 때문에 다른 블록으로 에러가 전파되지 않고 에러가 발생한 블록만 영향을 받는다.

2. CBC (Cipher Block Chaining)

CBC 운용모드는 ECB 운용모드의 취약점을 극복하기 위해 나온 것이다. 한 블록의 평문을 암호화하기 이전에, 이전의 평문이 암호화된 암호문과 XOR 연산을 하는 것이 특징이다. 맨 앞의 블록의 경우 이전의 암호문이 없기 때문에 IV (Initial Vector)를 사용하여 랜덤 초기화를 하는 것이 특징이다. CBC의 경우 암호화때는 병렬처리가 불가능하지만 복호화시에는 병렬처리가 가능하다. 에러전파의 경우 복호화시 암호문 $C_1$에 에러가 발생하면 $P_1$, $P_{i+1}$블록에 영향을 미치고 $P_{i+2}$블록 부터는 자기 복구(self recovering)을 통해 올바르게 동작한다.

3. CFB (Cipher FeedBack)

CFB 운용모드는 블록암호를 스트림암호로 변환한다. 평문과 이전 암호문이 암호화된 값과 XOR 연산을 통해 암호문이 생성된다. 초기에는 IV 값을 암호화하고 평문과 xor하여 암호문을 생성하는 것이 특징이다. CFB 운용모드는 평문과 암호문의 길이가 같아 별도의 정수배를 맞추는 패딩이 필요하지 않다. 복호화시에는 암호문을 알고있다는 가정하에 병렬처리가 가능하다. 에러전파는 CBC와 마찬가지로 암호문에 에러가 발생하면 해당 암호문에 해당하는 평문과 다음 평문에 영향을 미치게 되는 것이 특징이다.

4. OFB (Output FeedBack)

OFB 운용모드는 블록암호를 스트림암호로 변환한다. 평문과 암호문의 길이가 같아 패딩이 필요하지 않다. 동작 방식은 이전의 암호화된 값이 다시 암호화되어 평문과 XOR하여 암호문을 만들어낸다. 초기에는 IV 값을 암호화하여 평문과 다시 XOR한 뒤 암호문을 생성한다. 암호화와 복호화 과정이 동일하다는 특징을 가진다. OFB 모드에서는 평문과 관계없이 암호 알고리즘을 미리 돌려 XOR하기 위한 키스트림을 준비할 수 있는 것이 특징이다. 암호문에 1비트의 문제가 발생하면 대응되는 평문에 1비트의 에러가 발생한다.

5. CTR (CounTeR)

CTR 운용모드는 평문과 암호문의 길이가 같아 패딩이 필요하지 않다. 암호화와 복호화과정이 동일하다. 임의로 순서로 암호화와 복호화가 가능하다. Nonce와 Counter를 암호화하고 평문과 XOR하여 암호문을 만드는 것이 특징이다. 동일한 비밀키와 IV를 반복하여 사용할 경우 안전성에 문제가 생길 수 있다. 이러한 과정은 독립적으로 진행되어 병렬처리가 가능하다는 것이 특징이다. 암호문에 1비트의 문제가 발생하면 대응되는 평문에 1비트의 에러가 발생한다. EBC 모드 처럼 한 블록에서 생긴 에러가 다음 블록으로 전파 되지 않는다.

1. 양자 컴퓨팅

1.1 중첩과 얽힘

큐비트의 동작을 위해 중첩(superposition)과 얽힘(entanglement)이 필요하다.

먼저 중첩(superposition)이란 0과 1의 상태를 동시에 가지는 것을 의미한다. 지금의 컴퓨터는 0 또는 1로 표현되지만 중첩을 통해 0과 1의 상태를 동시에 가지고 있을 수 있다. 이러한 중첩과 관련해서 슈뢰딩거의 고양이라는 사고 실험이 있다. 처음 슈뢰딩거가 막스보른의 주장을 논파하기 위해 고안한 사고실험이었으나 오히려 역설적으로 양자역학을 가장 잘 설명한다.

얽힘(entanglement)은 단어 그대로 양자가 서로 얽혀있다는 것이다. 이 때 특징은 그 양자가 우주의 양 끝에 있어 멀리 떨어져 있더라도 연결이 되어 있고, 하나의 양자를 관측하는 순간 시공간의 제약을 넘어 빛의 속도 보다 빠르게 상태 정보가 반대쪽 양자에게 전달된다는 특징이 있다. 이를 양자의 비국소성이라고 한다.

2. 큐비트 설계

큐비트를 설계하기 위한 여러 방식이 있다. 크게 5가지 방식으로 나뉘며 종류는 초전도 루프를 이용한 큐비트 설계 방식, 이온 덫을 이용한 방식, 실리콘 양자점을 이용한 방식, 위상학 큐빗을 이용한 방식, 다이아몬드 점결합을 이용한 방식이 있다.

2.1 초전도 루프

초전도 루프 방식은 온도가 낮을수록 저항이 낮아진다는 방식을 이용하는 것이다. 금이나 구리는 아무리 차가워지더라도 항상 일정 수준의 저항을 보인다. 하지만 수은의 경우 다른 양상을 띠는데 수은을 4.2K까지 냉각시키면 저항이 0이 된다. 즉 수은은 전기저항이 0인 물질인 초전도체 물질이라 할 수 있다. 이외에도 임계 온도에서 저항이 0이되는 알루미늄, 갈륨, 니오븀 등이 있고 이러한 초전도체성을 띠는 물질을 이용하는 방식이 초전도 루프 방식이다.

초전도체의 가장 좋은 장점은 전기 손실이 없기 때문에 폐쇄 루프 내의 전류가 이론적으로 영원히 흐를 수 있다는 것이다. 실제로 초전도 링 위에서 전기를 수 년동안 흐르게 함으로써 실험적으로 입증된 바도 있다. 이러한 초전도 루프 방식의 또다른 장점은 오류 발생이 적다는 것이다. 약 99.4%의 논리 성공률을 보인다. 그리고 속도가 빠르고 기존의 재료 위에 구축이 가능하고, 2큐비트 연산을 수행할 수 있는 얽힘 큐빗의 개수가 9개로 적절하다고 한다. 하지만 단점으로는 크게 2가지인데 첫 번째로는 수명이 0.000005초에 불과하다는 것이다. 여기서 수명이란 상태 중첩이 유지될 수 있는 최소한의 시간을 의미한다. 두 번째로는 -271'C에서 보관해야 한다는 점이다.

이러한 초전도 루프 방식의 활용은 IBM 클라우드 플랫폼인 Q Experience에서 사용된다. 또한 구글 및 초전도체를 기반으로 실용 양자 컴퓨터의 제작을 목표로하는 벤처기업인 QCI도 이 방식을 채택한다.

2.2 이온 덫

이온 덫(ion trap)은 큐비트 내의 양자 상태를 제어하기 위한 기법이다. 이 방식은 초전도 루프 방식에 비해 얽힘을 저장하는 수명이 길다는 장점이 있다. 최대 1,000초까지 얽힘을 저장할 수 있다고 한다. 또한 성공률이 99.9%를 띠며, 2큐비트 연산을 수행할 수 있는 얽힌 큐비트의 개수가 14개로 가장 많다. 하지만 단점으로는 속도가 느리고, 많은 레이저가 필요하다. 이 기술을 활용하여 양자 컴퓨터를 만드려고 하는 선두주자는 미국 메릴랜드의 아이온큐(IonQ)이다.

2.3 실리콘 양자점

실리콘 양자점을 이용한 방식은 인텔(Intel)이 주도하고 있다. 실리콘 양자점을 이용하면 기존 반도체 재료 위에 구축되기 때문에 안정적이라는 장점이 있고 수명이 0.03초로서 초전도 루프방식에 비해 상대적으로 길다. 하지만 단점으로는 2큐비트 연산을 수행할 수 있는 얽힘 큐비트의 수가 2개로 적다는 것이다. 초전도 루프나 이온 덫에 비해 성공률이 낮지만 그럼에도 99%로 높은 편이다.

2.4 위상학 큐빗

위상학 큐빗을 이용한 방식은 양자 컴퓨터의 특징인 높은 오류 발생률을 낮추는데 중점을 둔 방식이다. 오류는 양자역학이 본질적으로 확률적이기 때문에 큐비트 얽힘의 지속시간으로 나타낼 수 있다. 위상한 큐빗은 아니온(anyon)이라는 2차원 준입자를 사용한다. 이 입자들은 서로 지나가면서 3차원 시공간에 끈(braid)을 형성하며, 그리고 이 끈들이 컴퓨터를 구성하는 논리 게이트를 형성한다.

이 방식의 장점은 안정적이고 오류가 없다. (수명이 적용되지 않음) 하지만 단점으로는 현 시점에서 순수하게 이론적 논의에 불과하다는 것이다. 다만 최근 실험으로는 현실에서도 절대 0도 근처의 낮은 온도와 강한 자기장에서 갈륨 비소로 만들어진 반도체를 사용하면 생성 가능할 것으로 확인되었다. 마이크로소프트와 벨 연구소가 이 설계 방식을 사용한다.

2.5 다이아몬드 점결합

다이아몬드 점결합의 경우 다이아몬드 표면에 있는 점결합을 이용하는 방식이다. 이 다이아몬드 점결합 방식의 가장 큰 장점은 -272도까지 온도를 낮출 필요 없이 실온에서 동작한다는 것이다. 또한 10초간의 긴 수명을 갖고 있고, 99.2%의 높은 성공률을 띤다. 2큐비트 연산을 수행할 수 있는 얽힘 큐비트의 수가 6개로 적당한 특징도 있다. 단점으로는 다이아몬드 표면의 약 2%에만 다이아몬드 점결합이 있다는 것이며, 얽힘을 만들기 어렵다는 점도 있다. 때문에 이러한 단점을 보완하기 위해 전자빔을 다이아몬드에 발사해 더 많은 결함을 생성시키는 연구가 이루어지고 있는 것이 특징이다.


결론적으로 이렇게 5가지 큐비트 설계 방식이 존재하며 현재까지는 초전도 루프 방식이 가장 앞서고 있다.

3. 트랜지스터와 양자 스케일

트랜지스터는 전자를 통과 혹은 차단하는 아주 작은 온오프 스위치다. 최근 트랜지스터는 크기가 14 나노미터로 분자크기와 비슷한 수준이다. 인류는 이러한 트랜지스터를 이용해서 컴퓨터나 의료장비나 항공우주 H/W 등에 사용했고 인류사회에 많은 기술적 진보를 가져왔다. 하지만 이 트랜지스터의 한계는 물리 법칙의 한계와 맞닿아 있다. 특히 양자역학이라는 건너기 힘든 벽에 직면하고 있다. 단위 면적당 트랜지스터를 몇 개나 집적할 수 있느냐에 따라 집적도가 결정된다. 따라서 트랜지스터의 크기를 가능한 작게 만드는 것이 중요하다. 트랜지스터의 크기는 1970년대 10마이크로미터, 1980년 후반에 1마이크로미터, 1990년대 나노미터에 이르렀다. 2020년의 트랜지스터의 크기는 약 5나노미터이다. (물 분자 크기 = 약 0.275 나노미터) 하지만 이렇게 점점 작게 만들수록 양자스케일이 문제가 된다.

양자스케일이란 일종의 treshold(역치)로, 거시적으로 영향을 미치는 고전역학의 효과와 미시적으로 영향을 미치는 양자역학의 효과를 가르는 거리를 의미한다. 이 경계는 100nm 이하의 범위 또는 초저온에서 발생하는데 현재 이 트랜지스터를 작게 만들수록 이러한 양자스케일 문제 해결이 어렵다는 것이다. 이러한 양자스케일에서 일어나는 현상인 양자 터널링 현상이 있다.

3.1 전자 터널링/양자 터널링

양자 터널링이란 고전적 스케일에서 넘어갈 수 없는 장벽을 양자 스케일에서 입자가 통과하는 현상이다. 양자 터널링은 전자 터널링은 같은 의미이며, 이는 트랜지스터에 큰 문제를 야기한다.

만약 위치 에너지가 V인 장벽을 에너지가 E인 입자가 넘어가려 한다면 고전적인 에너지 보존 법칙에 의해서 E>V가 되어야 장벽을 통과할 수 있으나 양자역학에 따르면 E<V라도 장벽을 통과할 수 있다는 것이다. 즉, 트랜지스터를 아무리 나노단위로 줄인다 하더라도 이러한 양자 터널링 현상 때문에 문제가 야기 된다.

4. 양자 컴퓨팅의 활용

양자 컴퓨터를 사용하면 여러 방면에 활용할 수 있다.

4.1 복잡한 시뮬레이션

지금의 고전 컴퓨터에서 무한히도 오래 걸릴 양자역학적 계를 양자 컴퓨터에서는 비교되지 않을 수준으로 시뮬레이션할 수 있다. 이런 시뮬레이션을 통해 가능할 것으로 보이는 것은 카오스적 현상의 설명이다. 예를 들어 지금의 기상청은 날씨를 정확하게 예측할 수 없다. 소수점이 조금만 달라지더라도 예측값이 완전히 달라지기 때문이다. 기상청은 여러 시뮬레이션을 통해 앙상블한 값을 기상 예보로 내고 있다. 만약 양자 컴퓨터를 사용하여 시뮬레이션 한다면 카오스에 숨겨진 역학을 통해 훨씬 더 높은 예측을 할 수 있을 것으로 판단된다.

4.2 분자 모델링과 신소재

양자 컴퓨터를 활용한다면 신약 개발에도 활용할 수 있다. 실제로 수소 원자 2개와 베릴륨 원자 1개로 구성되는 베릴륨 수소와 물 분자를 모델링한 바가 있다. 분자 모델링은 양자 컴퓨터의 새로운 응용 분야이다. 분자 모델링은 초창기에 지나지 않지만 화학 및 제약 회사에게는 미래가 유망한 분야다. 분자 시뮬레이션은 양자 컴퓨팅의 킬러 앱이 될 가능성이 높다.

4.3 정교한 딥러닝

딥러닝에서 사용하는 일부 최적화 문제는 문제 해결에 요구되는 상호작용 변수들의 수가 너무 많아 기존 하드웨어로는 접근하기 힘들다는 단점이 있다. 예시로 단백질 폴딩이나 우주선 비행 시뮬레이션 등이 있다. 양자 컴퓨터는 확률적 경사 하강법(stochastic gradient descent)을 사용해 최적화에 효율적으로 대처할 수 있다고 한다. D-wave라는 캐나다 기업은 Stochastic gradient descent을 사용해 최적화 문제를 해결하도록 특별히 설계된 양자 컴퓨터를 판매중에 있으며, 방산 업체인 록히트 마틴과 구글을 고객으로 하고 있다.

5. 양자 어닐링

먼저 어닐링이란 열처리 방법을 의미한다. 기존의 어닐링 방법은 열 에너지가 위치에너지를 뛰어넘어야 하지만 양자 어닐링은 뛰어넘지 않는 것을 의미한다. 양자 어닐링은 양자 컴퓨팅에 속하는 개념으로 제한적 양자 컴퓨팅이라 불리기도 한다. 양자 어닐링에서 사용되는 주요 개념 중 하나는 해밀토니안으로, 이는 모든 입자의 운동 에너지 및 양자역학계와 관련된 입자들의 위치 에너지 합계를 의미한다.

IBM Q와 같은 플랫폼은 큐빗 제어를 위해 논리게이트를 사용한다. 양자 어닐링 컴퓨터는 논리 게이트인 양자 게이트가 없기에 큐빗의 상태를 완전히 제어할 수 없다는 특징을 갖는다. 다만 단열 정리에 의해 큐빗의 동작을 예측할 수 있는데 이를 통해 에너지 최소화 문제를 해결할 때 유용하다는 특징이 있다. 다르게 말하면 양자 어닐링을 통해, 탐색 공간이 국소적 최소값에 이산적인 조합 최적화 문제에 주로 사용된다. 이러한 특징을 이용하는 회사가 디웨이브이다. 디웨이브의 시스템들은 큐빗이 에너지 상태를 최소화하는 경향이 있다는 것을 이용한다.

참고로 양자 어닐링을 통한 컴퓨팅에서의 단점은 쇼어알고리즘을 실행시킬 수 없으며 이는 큰 파장을 불러 일으킨 적 있다.

1. 기약 잉여계, 완전 잉여계, 오일러 함수 정의

기약 잉여계

• $\{a_1, a_2, \dots , a_m \}$가 법 $m$에 대한 완전 잉여계일 때, 여기서 $m$과 서로소인 원소만 모은 집합을 법 $m$에 대한 기약잉여계라 한다.

완전 잉여계

• $\{a_1, a_2, \dots , a_m \}$에서 $a \equiv a_i \pmod{m}$인 $a_i$가 유일하게 있을 때, $\{a_1, a_2, \dots , a_m \}$ 를 완전잉여계라고 한다.

오일러 정의

기약 잉여계 개념은 정수론에서 오일러의 정의를 증명하는 데 사용된다. 정수론에서 유용하게 쓰이는 정리로, 합동식과 관련이 있다. 페르마의 소정리를 일반화한 것이다.

• $a$와 $n$이 서로소인 양의 정수일 때, $a^{\varphi(n)} \equiv 1(mod\ n)$이다.
  • 여기서 $\varphi(n)$은 $1$부터 $n$까지의 정수 중 $n$과 서로소인 정수의 개수이다. 오일러 피 함수라고도 불린다.

• 양의 정수 $m$에 대하여, $m$ 이하의 자연수 중에서 $m$과 서로소인 정수의 개수를 $\varphi (m)$으로 나타내고 함수 $\varphi : Z→N$ 를 오일러의 $\varphi$ 함수라고 한다.
  
  • $\varphi$ = varphi

2. 확장 유클리드 알고리즘으로 곱셈의 역원 구하기

정의

유클리드 호제법이란 두 정수 사이에 최대공약수(GCD)를 보다 효과적으로 구하는 것으로, 인류 최초의 알고리즘이라 한다. 

두 개 자연수 $A, B$가 있고 $A\ \%\ B = r$이면 다음과 같다. (단, $A > B$)

$GCD(A,B) = GCD(B,r)$

이 때, $A\ \%\ B = r$에 의해 다음과 같은 식이 기본적으로 유도된다.

$A = Bq + r$

증명

두 자연수 $A,B (A > B)$의 최대공약수를 $G$라 하자. $G$는 공약수이므로 두 서로소 $a, b$에 대해 다음 식이 성립한다.

$A = aG, B = bG$

위의 식을 사용하여 $A = Bq + r$에 대입하면 다음과 같다.

$aG = bGq + r$

$r = aG - bGq$

$ r = (a - bq)G$

$A = aG, B = bG$에서 $a, b$가 서로소라면 $G$가 최대공약수이기 때문에 $b, a - bq$가 서로소임을 증명하면 된다.

이를 증명하기 위해서는 가정에 모순을 확인하는 귀류법을 사용하여 해결할 수 있다.

$b$와 $a - bq$가 서로소가 아니라면 두 수는 공약수 $k$를 가지기 때문에 다음과 같이 나타낼 수 있다.

$a - bq = mk$

$b = nk$

위 식의 항을 옮기고 대입하여 정리하는 과정은 다음과 같다.

$a = mk + bq$

$a = mk + nkq$

$a = (m+nq)k$

따라서 다음과 같은 식을 확인할 수 있다.

$a = (m+nq)k$

$b = nk$

하지만 $a$와 $b$는 서로소이나 공약수 $k$를 가지므로 거짓 명제이다.

따라서 $a-bq$와 $b$는 서로소이다.

3. 군환체 조건 정의 및 다항식체 모듈러 계산

군, 환, 체의 경우 대수학에서 사용되는 개념으로 기본적이면서 가장 중요한 개념으로 여겨진다.

군 환 체 정의

군

공집합이 아닌 집합 G 위에 다음 세 조건을 만족하는 이상연산 $\circ$가 정의될 때 $<G, \circ>$를 군이라 한다.

군의 공리

• 결합법칙 : $G$의 임의의 원소 $a, b, c$에 대해 다음이 성립한다.
  • $(a \circ b)\ \circ \ c\ =\ a\ \circ \ (b \circ c)$

• 항등원 : $G$의 모든 원소 $a$에 대해 다음이 성립하는 $e \in G$가 존재해야하며, 이 때 $e$를 $G$의 단위원 또는 항등원이라한다.
  • $a \circ e\ =\ e\circ a = a$

• 역원 : $G$의 각 원소 $a$에 대해 다음이 성립하는 $a^{-1}$이 $G$에 존재해야 하며, 이 때 $a^{-1}$를 $a$의 역원이라한다.
  
  • $a \circ a^{-1} = a^{-1} \circ a = e$

• 닫힘 : 어떤 집합의 임의의 두 원소(순서쌍)간에 연산이 행해질 때, 그 결과 역시 그 집합의 원소가 되는 것을 의미한다.
  • $a \circ b$ 연산의 결과도 집합 $G$에 속하며 순서쌍 $(a,b)$들의 곱(카테시안 곱) 연산에 대해 닫혀있음

군은 결합법칙, 항등원, 역원, 닫힘의 네 가지 특성을 가지고 있어야 한다.

군의 종류

• 가환군 or 아벨군
  • 군의 네 가지 특성에 추가적으로 교환법칙까지 성립할 경우 이를 아벨군(abelian group) 또는 가환군(commutative group)이라 한다.

• 순환군(Cyclic Group)
  
  • 한 원소로 군의 모든 원소를 표시할 수 있는 군을 의미하며, 이 때 해당 원소를 생성원(generator)라 한다.

• 덧셈군(Additive Group)
  
  • 군의 이항 연산이 덧셈 연산인 군

• 곱셉군(Muliplicative Group)
  
  • 군의 이항 연산이 곱셈 연산인 군

• 부분군(Subgroup)
  • 군 $G$의 부분집합으로 군 $G$와 같은 연산 구조를 가지는 군

군의 표기

• $(G, \circ)$ 또는 $<G, \circ>$ 또는 ${G, \circ}$
  • $G$: 군의 원소 집합
  • $\circ$ : 군의 연산
• 군의 차수/위수(order): $|G|$ 또는 $O(g)$ 또는 $G_n$ 또는 $ord(G)$로 나타낼 수 있다.

환

어떤집합 R 및 그 집합 위에 2개의 이항연산$(+, \circ)$이 정의되는 대수 구조를 의미하며 다음과 같이 표기한다.

• $(R, +, \circ)$ 또는 $< R, +, \circ>$ 또는 $환 R$

환의 공리

• 덧셈 연산에 대해 : $(R, +)$는 가환군
  • 닫혀 있음
  • 항등원(`0`)이 존재 $\rightarrow a + 0 = 0 + a = a$
• 각 성분에 대해 역원이 존재함$\rightarrow a + (-a) = (-a) + a = 0$

• 모든 성분에 대해 교환법칙이 성립 $\rightarrow a + b = b + a$

• 모든 성분에 대해 결합법칙이 성립 $\rightarrow (a + b) + c = a + (b + c)$

• 곱셈(\circ) 연산에 대해 : $(R, \circ)$
  • 닫혀 있음
  • 모든 성분에 대해 결합법칙이 성립 $\rightarrow (a\circ b)\circ c = a\circ (b\circ c)$
• 덧셈 및 곱셉 연산에 대해 : $(R, +, \circ)$
  • 모든 성분에 대해 분배법칙이 성립 $\rightarrow a\circ (b + c) = a\circ b + a\circ c, (a + b)\circ c = a\circ c + b\circ c$

추가적인 조건에 따른 환의 종류

• 가환환
  • 추가적으로 곱셈(\circ)에 대해서 가환이 되는 환 : $a \circ b = b \circ a)$

• 단위원을 갖는 환(Ring with Unity)
  • 추가적으로 곱셈 항등원 즉, 단위원을 갖는 환 : $1 \circ a = a \circ 1 = a$

• 나눗셈환
  • 단위원 1을 갖는 환으로써, 곱셈 역원이 존재하는 환 : 각 원소 $a \in R, a \neq 0$에 대해, $a \circ a^{-1} = a^{-1}\circ a = 1$

• 정역(Integraldomain)
  • 단위원 1을 갖는 가환환으로써, 추가적으로 다음 조건을 만족
    • $a \neq 0, b \neq 0$이면 $a \circ b \neq 0$을 만족함 또는
    • $a \circ b = 0$이면, $a = 0$ 또는 $b = 0$ $(a,b \in R)$

체

• 코드(부호) 등을 기술하는데 사용될 수 있는 수학적 대수 구조
  • 예) 실수 $R$, 유리수 $Q$, 복소수 $C$와 같은 수 체계에 대한 추상화
• 특정한 성질을 만족하는 2개의 연산이 정의되는 가환환
  • 그 요소들이 집합을 이루면서, 덧셈과 곱셈 연산 두 쌍을 사용할 수 있는 구조(2개 산술연산자)

체의 공리

• 덧셈 연산에 대해 : $<F, +>$
  • 집합 내 원소의 연산 결과가 다시 그집합 내에 있게된다. $\rightarrow$ 닫혀있음
  • 항등원 (`0`)이 존재 : $a + 0 = a = 0 + a$
  • 모든 성분에 대해 덧셈 역원이 존재 : $a + (-a) = 0 = (-a) + a$
  • 모든 성분에 대해 결합법칙이 성립 : $(a + b) + c = a + (b + c)$
  • 모든 성분에 대해 교환법칙이 성립 : $a + b = b +a$
• 곱셈 연산에 대해 : $<F, \circ>$
  • 모든 성분에 대해 분배법칙이 성립 : $a (b +c) = a b + a c$

위 체의 공리에서 덧셈 공리들 만을 만족할 경우는 아벨군 또는 가환군이며, 곱셈의 역원 존재 만을 제외한 나머지 공리들을 만족하는 경우는 환이다.

체의 공리가 성립하는 예제

• 실수체 : 실수 전체의 집합
• 복소수체 : 복소수 전체의 집합
• 유리수체 : 유리수 전체의 집합

유한개의 원소를 갖는 체 $\rightarrow$ 유한체(갈로이스체)

4. 중국인 나머지 정리

개요

중국인의 나머지 정리의 경우 연립 합동식의 해의 존재성과 유일성을 증명하는 정리이며 그 기원은 다음과 같다.

중국의 5세기 문헌인 『손자산경(孫子算經)』에는 다음과 같은 문제가 있다고 한다.

3으로 나누었을 때 2가 남고, 5로 나누었을 때 3이 남고, 7로 나누었을 때 2가 남는 수는 무엇인가?

정의

$gcd(n,m) = 1$면 $\begin {cases} x \equiv b\ (mod\ n) \\ x \equiv c\ (mod\ m) \end {cases}$는 $1 \leq x \leq nm$에서 단 하나의 해를 갖는다.

증명

$x \equiv b\ (mod\ n)$    (1)

$x \equiv c\ (mod\ m)$    (2)

$x \equiv b\ (mod\ n)$이므로 $x = ny + b$를 만족하는 $y \in Z$가 존재할 것이고, 이를 (2)에 대입하면 다음과 같다.

$ny \equiv c -b\ (mod\ m)$

위 정의에 의해 위 합동식은 $1 \leq y \leq m$에서 유일한 해 $y_0$를 갖고, 따라서 $x = ny_0 + b$는 $1 \leq x \leq nm$에서 유일한 해 $x_0$를 가진다. 따라서 다음과 같다.

$x_0 = ny_0 + b$

여기서 $x_0$는 (1)의 해다. 이제 $ny_0 \equiv c -b\ (mod\ m)$에 $ny_0 = x_0 - b$를 대입하면 다음과 같다.

$x_0 \equiv c\ (mod\ m)$

$x_0$은 (2)의 해가 된다. 증명 끝.

5. 가우스 소거법 / 가우스 조단 소거법

가우스 소거법을 이용하여 연립 방정식의 해를 구하는 과정이며, 아래에서 $R_2$는 2열을 의미한다.