For a better world

주성분 분석이란 무엇일까?

주성분 분석은 차원 축소에 사용되는 대표적인 알고리즘이다. 차원 축소는 고차원 공간 데이터를 저차원 공간으로 옮기는 것을 말한다. 그렇다면 이 차원축소가 왜 필요할까? 고차원으로 표현된 데이터는 계산 비용 많고 분석에 필요한 시각화가 어렵기 때문이다. 또 고차원을 이루는 피처 중 상대적으로 중요도가 떨어지는 피처가 존재할 수 있기 때문이다. 따라서 중요도가 낮은 피처를 제외하는 대신 계산 비용이나 비교적 준수한 성능을 얻는다. 주성분 분석을 진행하면 차원 축소로 인해 표현력이 일부 손실된다. 만약 4차원에서 2차원으로 축소를 통해 첫 번째 주성분과 두 번째 주성분을 얻고, 이 두 개가 원래 피처 표현력의 90%를 띤다면 나머지 10%의 손실을 감수하더라도 계산 효율을 얻게 된다. 

주성분 분석을 통해 저차원 공간으로 변환할 때 피처 추출(feature extraction)을 진행한다. 이는 기존 피처를 조합해 새로운 피처로 만드는 것을 의미한다. 이 때 새로운 피처와 기존 피처 간 연관성이 없어야 한다. 연관성이 없도록 하기 위해 직교 변환을 수행한다. 직교 변환을 수행하면 새로운 피처 공간과 기존 피처 공간이 90도를 이루게 된다. 즉 내적하면 0이 되는 것이다. 이러한 직교 변환을 수행할 때 기존 피처와 관련 없으면서 원 데이터의 표현력을 '잘' 보존해야 한다. 잘 보존하는 것은 주성분 분석의 핵심인 분산(Variance)을 최대로 하는 주축을 찾는 것이다.

여기서 분산이란? 데이터가 퍼진 정도를 의미한다. 예를 들어 만약 4차원 공간이 있고 3차원 공간으로 차원 축소를 한다면 3차원 공간상에서 데이터 분포가 넓게 퍼지는, 즉 분산을 가장 크게 만드는 벡터를 찾아야 한다. 만약 3차원 공간이 있고 2차원 공간으로 차원 축소한다면, 2차원 공간상에서 데이터 분포가 가장 넓게 퍼지도록 하는 벡터를 찾아야 한다. 만약 2차원 공간이 있고 1차원 공간으로 차원 축소 한다면 1차원 공간상에서 데이터 분포가 가장 넓게 퍼지게 만드는 벡터를 찾아야 한다.

애니메이션으로 이해하자면 다음과 같다. 

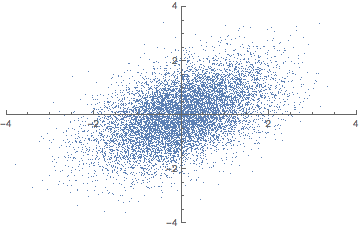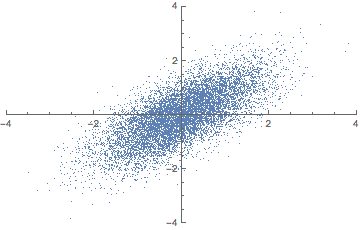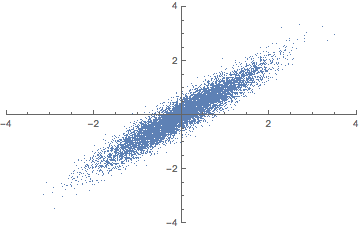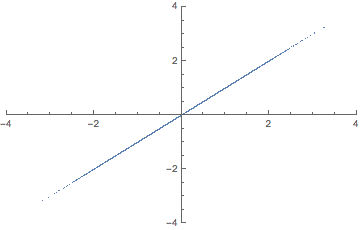
2차원 공간을 1차원으로 줄일 때 2차원에 넓게 퍼진 데이터 분포를 1차원 상에서도 똑같이 넓게 퍼질 수 있도록 하는 "벡터"를 찾아야 한다. 여기서 "벡터"는 곧 주축을 의미한다. 이 때 주축과의 동의어를 Eigen vector라고 한다. 주축을 찾고 주축에 피처들을 사상시키게 되면 주성분이 된다. 다르게 말해 피처들을 주축에 사상시킬 때 분산이 최대가 되는 주성분이 만들어진다. 이렇게 분산이 가장 큰 주성분을 첫 번째 주성분, 두 번째로 큰 축을 두 번째 주성분이라 한다. 

그렇다면 이 주축인 Eigen vector는 어떻게 구하고, Eigen vector에 피처를 어떻게 사상시킬수 있는 것일까? Eigen vector를 구하기 위해서는 특이값 분해 (SVD, Singular Value Decomposition)가 수행된다. 또 사상을 위해서 공분산 행렬이 필요하다. 따라서 사실상 PCA를 한마디로 말하면 데이터들의 공분산 행렬에 대한 특이값 분해(SVD)로 볼 수 있다. 먼저 공분산 행렬에 대해 알아보자.

공분산 행렬이란 무엇일까?

공분산은 한 마디로 두 피처가 함께 변하는 정도, 즉 공변하는 정도를 나타낸다. 수식으로 표현하면 다음과 같다.

$\sum = Cov(X) = {X^TX\over n}$

여기서 n은 행렬 X에 있는 데이터 샘플 개수를 나타내며 $X$란 전체 피처와 데이터 값을 나타낸다. X의 열축은 피처가 되고 X의 행축은 데이터 개수가 된다. 예를 들어 $x_1, x_2, x_3 $ 피처 3개가 있다고 가정하면 $X^T \times T$는 아래와 같이 표현할 수 있다. 

$X^T \times X = $ $\begin{vmatrix} 0.1 & 0.4 & 0.7 \\ 0.2 & 0.5 & 0.8 \\ 0.3 & 0.6 & 0.9 \end{vmatrix}$ $\times$ $\begin{vmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9 \end{vmatrix}$

전치 행렬과 행렬을 내적하게 되면  아래와 같은 대칭 행렬이 만들어진다.

$\begin{vmatrix} dot(x_1,x_1) & dot(x_1,x_2) & dot(x_1,x_3) \\ dot(x_2,x_1) & dot(x_2,x_2) & dot(x_2,x_3) \\ dot(x_3,x_1) & dot(x_3,x_2) & dot(x_3,x_3) \end{vmatrix}$

이 행렬에서 모든 대각 성분은 같은 피처 간 내적이므로 분산에 해당한다. 대각 성분 이외에는 모두 다른 피처 간 내적이므로 공분산에 해당한다. 즉 이러한 피처 간 내적을 통해 수치적으로 i번 피처와 j번 피처가 공변하는 정도를 알 수 있게 된다. 이것이 수식이 나타내는 의미이다. 수식에서 n으로 나눈 것은 공분산이 커질 수 있으므로 데이터 개수로 나누어 평균을 구한 것이다. 이렇게 만들어진 행렬을 공분산 행렬이라 한다. 

공분산 행렬이 가지는 의미는 무엇이고 어떻게 활용할까?

공분산 행렬은 피처 간에 서로 함께 변하는 정도를 의미한다고 했다. 공분산 행렬은 이러한 공변의 의미와 더불어 한 가지 의미가 더 있다. 그 의미는 바로 벡터에 선형 변환(사상)을 가능하게 하는 것이다. 즉, 공간상에 한 벡터가 있을 때 공분산 행렬을 곱해주게 되면 그 벡터의 선형 변환이 이루어진다. 이는 선형대수학에서 행렬이 벡터를 선형 변환시키는 역할을 하기 때문이다. 즉 공분산 행렬엔 피처간 공변 정보가 담겨 있으므로 이를 주축인 Eigen vector에 사상시키면 주성분을 구할 수 있다. 다음으로 주축을 구하기 위한 특이값 분해(SVD)를 살펴보자.

특이값 분해란 무엇이며 이를 통해 어떻게 Eigen vector를 구할 수 있을까?

먼저 특이값 분해란 일종의 행렬에서 이뤄지는 인수 분해다. 정확히는 행렬을 대각화하는 방법 중 하나이다. 대각화하는 이유는 대각화된 행렬의 대각선에 있는 값이 특이값(Singular Value)에 해당하기 때문이다. PCA에서 특이값 분해 대상은 위에서 본 공분산 행렬이다. 공분산 행렬을 특이값 분해 함으로써 PCA에 필요한 주축인 Eigen vector와, Eigen vector 스케일링에 필요한 Eigen value를 얻을 수 있다. Eigen value를 얻은 뒤 내림차순으로 정렬했을 때 가장 첫 번째 값이 분산을 최대로 하는 값이다.

일반적으로 특이값 분해는 고유값 분해(EVD)와 함께 설명된다. 고유값 분해의 경우 m x m의 정방 행렬에서만 사용할 수 있지만, 특이값 분해의 경우 m x n 인 직사각 행렬에도 적용가능하다. 따라서 일반화가 가능하단 장점이 있다. 또 특이값이란 고유값에 루트를 씌운 값이다. 그렇다면 특이값 분해는 어떻게 진행될까? 먼저 실수 공간에서 임의의 m x n 행렬에 대한 특이값 분해는 다음과 같이 정의된다.

$ A = U\sum V^T$

수식 성분이 나타내는 바는 다음과 같다. 참고로 여기서 $\sum$이란 합을 의미하는 기호가 아니라 행렬을 의미한다. 

$A = m \times n $ 직사각 행렬 (diagonal matrix)

$U = m \times m $ 직교 행렬 (orthogonal matrix)

$\sum = m \times n$ 직사각 대각행렬 (diagonal matrix)

$V = n \times x $ 직교 행렬 (orthogonal matrix)

특이값 분해를 이해하기 앞서 두 가지 선형대수적 특성을 알아야 한다. 첫 번째는 $U$, $V$가 직교 행렬이라면 선형대수적 특성에 의해 $UU^T = VV^T = E$, $U^{-1} = U^T, V^{-1} = V^T$가 만족한다는 것이다. 여기서 $E$는 항등행렬이다. 여기서 항등행렬이란 가령 $U$에 역행렬인 $U^{-1}$를 곱했을 때 나오는 행렬을 의미한다. 두 번째론 대칭 행렬은 고유값 분해가 가능하며 또 직교행렬로 분해할 수 있다는 것이다. 앞에 보았던 공분산인 행렬 $A$는 대각선으로 기준으로 값들이 대칭을 띠는 대칭 행렬이었다. 그러므로 고유값 분해 또는 직교행렬로 분해할 수 있다. 또 행렬 $A$가 대칭행렬이므로 $A^T$도 대칭 행렬이다.

결과적으로 PCA는 특이값 분해를 통해 $\sum$를 구하고자 한다. 이 $\sum$는 $AA^T, A^TA$를 고유값 분해해서 나오는 고유값들에 루트를 씌운 값들이 대각선에 위치하는 행렬이다. 그리고 $AA^T$와 $A^TA$의 고유값이 같다. 이를 증명하는 하는 과정은 다음과 같다.

앞서 특이값 분해의 정의는 $A = U\sum V^T$라고 했다. 이때 $A$는 대각행렬이므로 고유값 분해가 가능하다. 

$AA^T = (U\sum V^T)(U\sum V^T)^T$

            $= U\sum V^T V\sum^T U^T$ (이 때 $V^TV$ = $V^{-1}V$ 즉 직교행렬이므로 항등 행렬이 되어 사라짐)

            $= U(\sum \sum^T)U^T$

즉 $AA^T$를 고유값 분해하면 = $U(\sum \sum^T)U^T$가 된다. 또,

$A^TA = (U\sum V^T)^T(U\sum V^T)$

            $= V\sum^T U^TU\sum V^T$ (이 때 $U^TU$ = $U^{-1}U$ 즉 직교행렬이므로 항등 행렬이 되어 사라짐)

            $= V(\sum ^T\sum)V^T$

즉 $A^TA$를 고유값 분해하면 = $ V(\sum ^T\sum)V^T$가 된다.

그리고 이를 정리하고 덧붙이면,

$U$는 $AA^T$를 고유값 분해 해서 얻은 직교행렬이다. 그리고 U의 열벡터를 A의 left singular vector라 부른다.

$V$는 $A^TA$를 고유값 분해 해서 얻은 직교행렬이다. 그리고 V의 열벡터를 A의 right singular vector라 부른다.

$\sum$은 $AA^T, A^TA$를 고유값 분해해서 나온 고유값($\lambda$, eigen value)들의 제곱근을 대각원소로 하는 직사각 대각행렬이다. 

이 $\sum$의 대각원소들을 행렬 A의 특이값(singular value)라 부른다. 아래 수식과 같다. 

$\begin{vmatrix} \sqrt\lambda_1 & 0 & 0 & \dots \\ 0 & \sqrt\lambda_2 & 0 & \dots \\ 0 & 0 & \sqrt\lambda_3 & \dots \\ 0 & 0 & 0 & \dots \end{vmatrix}$

* 참고로 $\sum$의 경우 직사각 대각행렬이므로 m > n이거나 m < n인 경우로 나뉜다. 이 두 경우 모두 항상 대각선에만 특이값이 있어야 한다는 점만 상기하면 혼동되지 않는다. 

특이값들($\sum\sum^T or \sum^T\sum)$을 제곱하게 되면 $AA^T, A^TA$의 고유값과 같다.

결국 특이값 분해를 수행하게되면 $AA^T$와 $A^TA$의 고유벡터와, 고유값이 도출된다.

이후 고유벡터의 방향으로 피처들을 사상시키고, 고유값의 크기만큼 스케일링 해줌으로써 PCA 과정이 마무리 된다.

Reference

[1] Eigen Vector, Eigen Value: https://m.blog.naver.com/galaxyenergy/222123501087

[2] Covariance, SVD: https://www.youtube.com/watch?v=jNwf-JUGWgg 

[3] SVD: https://blog.naver.com/galaxyenergy/222865992256

[4] SVD: https://rfriend.tistory.com/185

[5] SVD: https://darkpgmr.tistory.com/106

[6] Image: https://medium.com/vlgiitr/principal-components-analysis-82a7682323e6

차원 축소란?

차원축소는 매우 많은 피처로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성하는 것이다. 일반적으로 차원이 증가할수록 데이터 포인트 간의 거리가 기하급수적으로 멀어지게 되고, 희소(sparse)한 구조를 가지게 된다. 수백 개 이상의 피처로 구성된 데이터 세트의 경우 상대적으로 적은 차원에서 학습된 모델보다 예측 신뢰도가 떨어진다. 또한 피처가 많을 경우 개별 피처간에 상관관계가 높을 가능성이 크다. 선형 회귀와 같은 선형모델에서는 입력 변수 간의 상관관계가 높을 경우 이로 인한 다중 공선성 문제로 모델의 예측 성능이 저하된다.

다차원의 피처를 차원 축소해 피처 수를 줄이면 더 직관적으로 데이터를 해석할 수 있다. 가령 수십 개 이상의 피처가 있는 데이터의 경우 이를 시각적으로 표현해 데이터의 특성을 파악하기는 불가능하다. 이 경우 3차원 이하의 차원 축소를 통해서 시각적으로 데이터를 압축해서 표현할 수 있다. 또한 차원 축소를 할 경우 학습 데이터의 크기가 줄어들어서 학습에 필요한 처리 능력도 줄일 수 있다.

일반적으로 차원 축소는 피처 선택(feature selection)과 피처 추출(feature extraction)로 나눌 수 있다. 피처 선택, 즉 특성 선택은 말 그대로 특정 피처에 종속성이 강한 불필요한 피처는 아예 제거하고, 데이터의 특징을 잘 나타내는 주요 피처만 선택하는 것이다. 피처 추출은 기존 피처를 저차원의 중요 피처로 압축해서 추출하는 것이다. 이렇게 새롭게 추출된 중요 특성은 기존의 피처가 압축된 것이므로 기존의 피처와는 완전히 다른 값이 된다.

피처 추출은 기존 피처를 단순 압축이 아닌, 피처를 함축적으로 더 잘 설명할 수 있는 또 다른 공간으로 매핑해 추출하는 것이다. 가령 학생을 평가하는 다양한 요소로서 모의고사 성적, 종합 내신성적, 수능성적, 봉사활동, 대외활동, 학교 내외 수상경력 등과 관련된 여러 가지 피처로 돼 있는 데이터 세트라면 이를 학업 성취도, 커뮤니케이션 능력, 문제 해결력과 같은 더 함축적인 요약 특성으로 추출할 수 있다. 이러한 함축적인 특성 추출은 기존 피처가 전혀 인지하기 어려웠던 잠재적인 요소(Learning Factor)를 추출하는 것을 의미한다. (위의 학생 평가 요소는 함축적 의미를 인지하기 어려운 것은 아니나, 함축성의 예시를 든 것이다)

차원 축소는 단순히 데이터의 압축을 의미하는 것이 아니다. 더 중요한 의미는 차원 축소를 통해 좀 더 데이터를 잘 설명할 수 있는 잠재적인 요소를 추출하는 데에 있다. PCA, SVD, NMF는 이처럼 잠재적인 요소를 찾는 대표적인 차원 축소 알고리즘이다. 매우 많은 차원을 가지고 있는 이미지나 텍스트에서 차원 축소를 통해 잠재적인 의미를 찾아 주는 데 이 알고리즘이 잘 활용된다.

차원 축소 알고리즘은 매우 많은 픽셀로 이뤄진 이미지 데이터에서 잠재된 특성을 피처로 도출해 함축적 형태의 이미지 변환과 압축을 수행할 수 있다. 이렇게 변환된 이미지는 원본 이미지보다 훨씬 적은 차원이기 때문에 이미지 분류 등의 분류 수행 시에 과적합 영향력이 작아져서 오히려 원본 데이터로 예측하는 것보다 예측 성능을 더 끌어 올릴 수 있다. 이미지 자체가 가지고 있는 차원의 수가 너무 크기 때문에 비슷한 이미지라도 적은 픽셀의 차이가 잘못된 예측으로 이어질 수 있기 때문이다. 이 경우 함축적으로 차원을 축소하는 것이 예측 성능이 훨씬 도움이 된다.

차원 축소 알고리즘이 자주 사용되는 또 다른 영역은 텍스트 문서의 숨겨진 의미를 추출하는 것이다. 문서는 많은 단어로 구성돼 있다. 일반적으로 사람의 경우 문서를 읽으면서 이 문서가 어떤 의미나 의도를 가지고 작성됐는지 쉽게 인지할 수 있다. 차원 축소 알고리즘은 문서 내 단어들의 구성에서 숨겨져 있는 시맨틱(Semantic) 의미는 토픽(Topic)을 잠재 요소로 간주하고 이를 찾아낼 수 있다. SVD와 NMF는 이러한 시맨틱 토픽(Semantic Topic) 모델링을 위한 기반 알고리즘으로 사용된다.

PCA

PCA (Principal Component Analysis)는 가장 대표적인 차원 축소 기법이다. PCA는 여러 변수 간에 존재하는 상관관계를 이용해 이를 대표하는 주성분(Principal Component)을 추출해 차원을 축소하는 기법이다. PCA로 차원을 축소할 때는 기존 데이터의 정보 유실이 최소화되는 것이 당연하다. 이를 위해 PCA는 가장 높은 분산을 가지는 데이터의 축을 찾아 이 축으로 차원을 축소하는데, 이것이 PCA의 주성분이 된다(즉, 분산이 데이터의 특성을 가장 잘 나타내는 것으로 간주한다) 키와 몸무게 2개의 피처를 가지고 있는 데이터가 세트가 있다고 가정하면 아래와 같은 방식으로 축소를 진행한다.

위와 같이 키와 몸무게라는 피처가 2개 있을 때 1개의 주성분을 가진 데이터 세트로 차원 축소를 한다. 데이터 변동성이 가장 큰 방향으로 축을 생성하고, 새롭게 생성된 축으로 데이터를 투영하는 방식이다. PCA는 제일 먼저 가장 큰 변동성(Variacne)을 기반으로 첫 번째 벡터 축을 생성하고, 두 번째 축은 이 벡터 축에 직각이 되는 벡터(직교 벡터)를 축으로 한다. 세 번째 축은 다시 두 번째 축과 직각이 되는 벡터를 설정하는 방식으로 축을 생성한다. 이렇게 생성된 벡터 축에 원본 데이터를 투영하면 벡터 축의 개수만큼의 차원으로 원본 데이터가 차원 축소된다. (긴 벡터가 첫 번째  PCA 축, 짧은 벡터가 두번째 PCA 축)

PCA, 즉 주성분 분석은 이처럼 원본 데이터에 피처 개수에 비해 매우 작은 주성분으로 원본 데이터의 총 변동성을 대부분 설명할 수 있는 분석법이다.

PCA를 선형대수 관점에서 해석해 보면, 입력 데이터의 공분산 행렬(Covariance Matrix)을 고유값 분해하고, 이렇게 구한 고유벡터에 입력 데이터를 선형 변환하는 것이다. 이 고유벡터가 PCA의 주성분 벡터로서 입력 데이터의 분산이 큰 방향을 나타낸다. 고유값(eigenvalue)은 바로 이 고유벡터의 크기를 나타내며, 동시에 입력 데이터의 분산을 나타낸다. 

일반적으로 선형 변환은 특정 벡터에 행렬 A를 곱해 새로운 벡터로 변환하는 것을 의미한다. 이를 특정 벡터를 하나의 공간에서 다른 공간으로 투영하는 개념으로도 볼 수 있고, 이 경우 이 행렬을 바로 공간으로 가정하는 것이다.

보통 분산은 한 개의 특정한 변수의 데이터 변동을 의미하나, 공분산은 두 변수 간의 변동을 의미한다. 즉, 사람 키 변수를 X, 몸무게 변수를 Y라고 하면 공분산 Cov(X, Y) > 0은 X(키)가 증가할 때 Y(몸무게)도 증가한다는 의미다. 공분산 행렬은 여러 변수와 관련된 공분산을 포함하는 정방형 행렬이다.

위 표에서 보면 공분산 행렬에서 대각선 원소는 각 변수(X, Y, Z)의 분산을 의미하며, 대각선 이외의 원소는 가능한 모든 변수 쌍 간의 공분산을 의미한다. X, Y, Z의 분산은 각각 3.0, 4.5, 0.91이다. X와 Y의 공분산은 -0.71, X와 Z의 공분산은 -0.24, Y와 Z의 공분산은 0.28이다. (덧붙여 공분산이 0이라면 두 변수 간에는 아무런 선형 관계가 없으며 두 변수는 서로 독립적인 관계에 있다. 그러나 두 변수가 독립적이라면 공분산은 0이 되지만, 공분산이 0이라고 해서 항상 독립적이라할 수 없다.)

고유벡터는 행렬 A를 곱하더라도 방향이 변하지 않고 그 크기만 변하는 벡터를 지칭한다. 즉, Ax = ax(A는 행렬, x는 고유벡터, a는 스칼라값)이다. 이 고유벡터는 여러 개가 존재하며, 정방 행렬은 최대 그 차원 수만큼의 고유벡터를 가질 수 있다. 예를 들어 2x2 행렬은 두 개의 고유벡터를, 3x3 행렬은 3개의 고유벡터를 가질 수 있다. 이렇게 고유벡터는 행렬이 작용하는 힘의 방향과 관계가 있어서 행렬을 분해하는 데 사용된다.

공분산 행렬은 정방행렬(Diagonal Matrix)이며 대칭행렬(Symmetric Matrix)이다. 정방행렬은 열과 행이 같은 행렬을 지칭하는데, 정방행렬 중에서 대각 원소를 중심으로 원소 값이 대칭되는 행렬, 즉 $A^T = A$인 행렬을 대칭행렬이라 부른다. 공분산 행렬은 개별 분산값을 대각 원소로 하는 대칭행렬이다. 이 대칭행렬은 고유값 분해와 관련해 매우 좋은 특성이 있다. 대칭행렬은 항상 고유벡터를 직교행렬(orthogonal matrix)로, 고유값을 정방 행렬로 대각화할 수 있다는 것이다.

입력 데이터의 공분산 행렬 C라고 하면 공분산 행렬의 특성으로 인해 다음과 같이 분해할 수 있다.

$C = P \sum P^T$

이때 $P$는 n x n의 직교행렬이며, $\sum$은 n x n 정방행렬, $P^T$는 행렬 $P$의 전치 행렬이다. 위 식은 고유벡터 행렬과 고유값 행렬로 다음과 같이 대응된다.

$C = \begin{bmatrix} e_1 \dots e_n \end{bmatrix} \begin{bmatrix} \lambda_1 & \dots & 0 \\ \dots & \dots & \dots \\ 0 & \dots & \lambda_n \end{bmatrix} \begin{bmatrix} e{_1}^t \\ \dots \\ e{_n}^t \end{bmatrix}$

즉, 공분산 C는 고유벡터 직교 행렬 * 고유값 정방 행렬 * 고유벡터 직교 행렬의 전치 행렬로 분해된다. $e_i$는 $i$번째 고유벡터를, $\lambda_i$는 $i$번째 고유벡터의 크기를 의미한다. $e_1$는 가장 분산이 큰 방향을 가진 고유벡터이며, $e_2$는 $e_1$에 수직이면서 다음으로 가장 분산이 큰 방향을 가진 고유벡터이다.

선형대수식까지 써가면서 강조하고 싶었던 것은 입력 데이터의 공분산 행렬이 고유벡터와 고유값으로 분해될 수 있으며, 이렇게 분해된 고유벡터를 이용해 입력 데이터를 선형 변환하는 방식이 PCA라는 것이다. 보통 PCA는 다음과 같은 단계로 수행된다.

1. 입력 데이터 세트의 공분산 행렬을 생성
2. 공분산 행렬의 고유벡터와 고유값을 계산
3. 고유값이 가장 큰 순으로 K개(PCA 변환 차수만큼)만큼 고유벡터를 추출
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력 데이터를 변환

Reference

[1] 파이썬 머신러닝 완벽가이드

[2] https://csleoss.etri.re.kr/images/contents/manual_1.0/operator/4.1.1.23.PCA_manual.html

[3] https://ko.wikipedia.org/wiki/주성분_분석