[선형대수학] 벡터, 기저, 스팬 (Vector, Basis and Span)

선형대수학을 볼 때마다 느끼지만 대수적으로만 기술되어 있다보니 늘 추상적으로 느껴지고 직관적이지가 않았습니다. 이번에 국문과 공대생이라는 블로그를 운영하시는 분의 글을 보다가 명불허전이라는 분의 선형대수 강의를 수강하고보니 선형대수 이해를 이렇게 잘 알려주는 사람이 있구나 하면서 감탄했습니다. 아무래도 선형대수에서 흔히 배우는 방식인 대수적인 측면이외에도 기하적인 측면의 설명과 더불어 시각화 자료가 높은 이해도의 핵심을 차지 한 것 같습니다. 

 

늘 선형대수를 보며 그래서 대체 물리와 어떻게 연결해 설명할 수 있는 것인지 궁금했습니다. 중고등학교때 함수나 미적분을 왜 배우는지 몰랐지만 지나고나니 물리학에서 파동을 기술하거나 다른 물리량을 알아내는 데에 쓰인다는 것을 알게 되었고, 수학으로 물리학을 말할 수 있다는 사실이 흥미로워지면서 더 관심을 갖게 됐습니다. 마찬가지로 선형대수도 물리학적으로 가지는 의미를 이해하면 더 이해가 높아질 것 같아서 그런 강의가 없을까 했는데 3Blue1Brown라는 유튜버의 강의를 접하고나서 많이 해소가 된 것 같습니다.

 

링크는 https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab 입니다. 총 16강으로 구성되어 있구요 각 강의는 10분대 내외로 짧게 이루어집니다. 서두가 길어지면서 홍보글 같긴하네요. 아무튼 강추합니다. 

 

첫 강의에서부터 선형대수를 바라볼 수 있는 3가지 측면을 언급하면서 시작합니다. 물리학의 관점, 컴퓨터 과학의 관점, 수학의 관점이 있다고 이야기합니다. 선형대수에서 자주 쓰이는 벡터는 물리학의 관점에서 화살표와 동일하며, 컴퓨터과학에서는 숫자 리스트, 수학의 관점에서는 모든 것이라 이야기합니다. 관점으로는 간단히 여기까지만 이야기하고 이후로는 선형대수의 개념에 대해 설명을 진행합니다. 저는 물리 이외에도 (당연하지만) 컴퓨터과학과 수학의 관점에서 바라볼 수 있다고 언급한 것에서 넘어가서 계속 보게 된 것 같습니다.

 

기초 벡터 연산

선형대수학에서는 크게 두 가지 기본적인 연산으로 이루어집니다. 벡터 합과 스칼라곱입니다. 벡터는 단순합니다. 화살표라고 생각해도 됩니다. 또는 화살표의 좌표를 나타내는 것이라 생각하면 됩니다. 이후 강의를 통해 스칼라의 의미를 처음으로 제대로 이해하게 됐습니다. 

 

 

스칼라는 단순히 숫자로만 이해하고 있었으나 위와 같이 하나의 벡터(화살표)의 길이를 늘리거나 줄이거나 방향을 바꾸는 것을 Scaling이라 하는데, 위의 그림과 같이 2, 1/3, -1.8과 같이 벡터 스케일링에 사용되는 숫자들을 스칼라(scalar)라고 한다고 합니다. (스칼라의 영어발음이 스케일라였습니다.) 즉 선형대수에서 스칼라는 벡터 스케일링을 목적으로 사용됩니다.

 

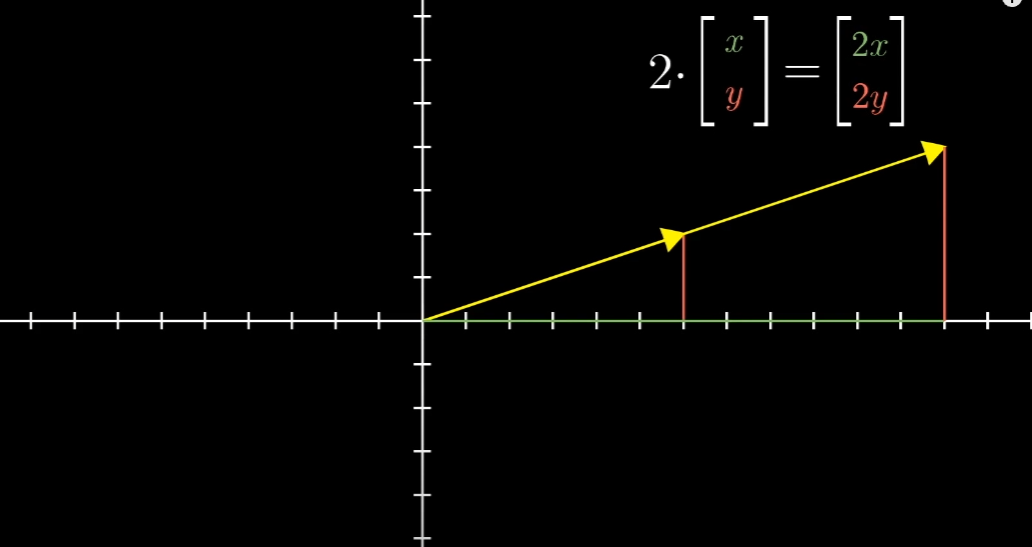
벡터에 스칼라를 곱하는 것은 숫자 리스트(행렬)라는 개념에서 리스트의 각 원소에 숫자를 곱하는 것과 같습니다. 스칼라를 이용해 벡터를 스케일링할 수 있고 이렇게 스케일링된 두 벡터끼리 더하는 것을 선형결합(linear combination)이라고 합니다. 

 

기저

기저 또한 처음으로 시원하게 강의를 듣게 되어 이해할 수 있었습니다. 기저를 설명하기 위해서는 먼저 2차원 x, y 좌표계상의 특별한 두 가지 벡터가 있다고 합니다. 바로 x축에 있는 단위 벡터(unit vector)인 $\hat{i}$와 y축에 있는 단위 벡터인 $\hat{j}$입니다. 이 둘을 좌표계의 기저(basis)라고 합니다. 

 

 

그렇다고하면 이 기저는 어떤 의미를 가지는가?라고 했을 때 핵심은 벡터의 변환을 구할 수 있다는 것입니다. 조금 더 설명하면 어떤 벡터 $(x, y)$가 있을 때 어떤 행렬을 거쳐서 공간상에 $(x', y')$로 매핑된다면 그 기저는 어떤 행렬이 되는 것입니다. 즉 Input vector $(x, y)$는 기저만 알고 있다면 바로 output vector $(x', y')$를 도출해낼 수 있는 것과 같습니다. 조금 더 자세히 말해 벡터가 행렬로부터 변환이 된다면 벡터를 이루는 기저 또한 변환이 되는데 결과적으로 변환된 기저벡터를 알고 있다면 어떤 벡터 $(x, y)$가 와도 변환을 바로 시킬 수 있다는 것입니다. (보충 설명은 앞으로 작성될 선형변환 포스팅에서 참고 바랍니다)

 

이 기저라고 하는 것은 암묵적으로 원점을 기준으로 하는 것으로 사용하고 있습니다. 때문에 움직이는 것은 두 벡터만 움직입니다. 두 벡터를 가지고 어디에 활용할까요? 아래와 같이 2차원 공간상의 모든 좌표를 표현할 수 있게 됩니다. 무한하고 평평한 2차원 평면을 만들 수 있다는 것입니다. 

 

 

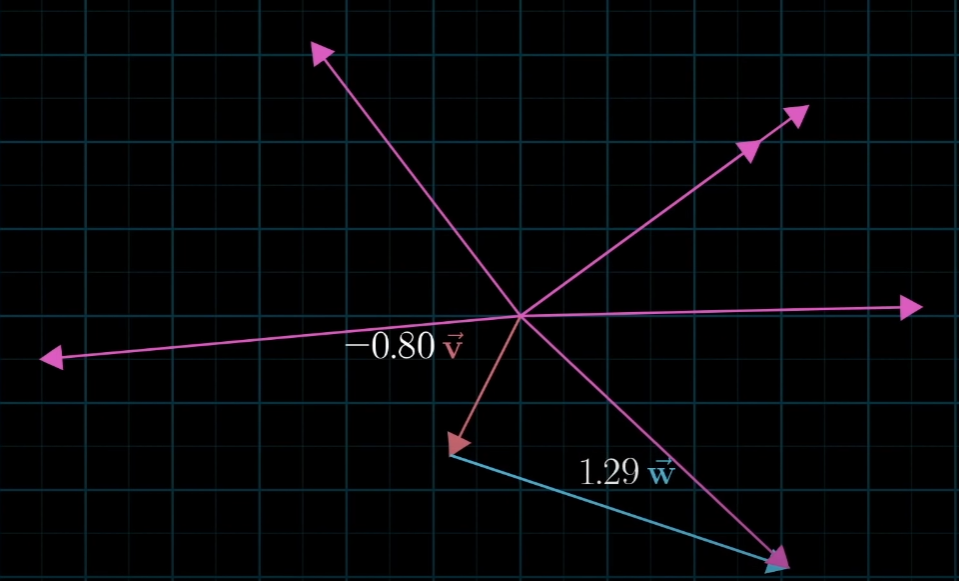
이렇게 두 벡터를 통해 표현할 수 있는 공간을 Span이라고 합니다. 정확히 Span의 사전적 정의는 주어진 두 벡터 쌍의 조합으로 나타낼 수 있는 output vector의 집합입니다. 2차원 벡터쌍의 span은 대부분 2차원 공간 전체가 됩니다. 

 

하지만 이러한 span이 특정 선 위로 제한이 되는 경우도 있습니다. 바로 두 벡터 중 하나가 다른 벡터와 겹치게 되는 경우 입니다.

 

 

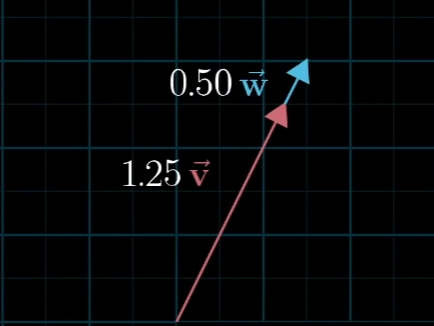
이럴 때는 Span이 2차원 공간이 아니라 단순히 직선 하나로 볼 수 있습니다. 이렇게 하나의 벡터가 다른 벡터에 겹치게 되어 Span이 한 차원 확장되지 못하는 경우를 선형 종속(Linear Dependent)이라고 합니다. 다시 말해 벡터가 하나만 있었다면 1차원 선만 표현하지만 2개라면 2차원을 표현해야합니다. 하지만 2개의 벡터가 있음에도 불구하고 1차원 밖에 표현하지 못하는 것을 의미합니다. 

 

반대로 하나의 벡터를 추가하여 기존 Span이외에 다른 차원을 추가해주는 것이 가능하다면 선형 독립(Linear Independent)라고 합니다. 이는 3차원에서도 마찬가지입니다.

 

 

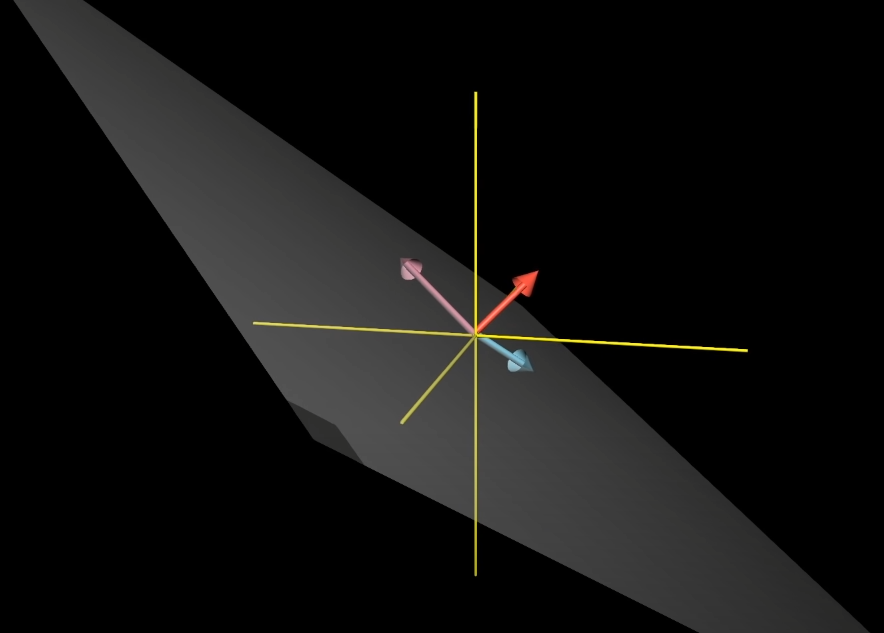
세 개의 벡터가 있을 때 스팬은 모든 가능한 선형결합의 결과집합입니다. 즉, 세 개의 벡터로 모든 3차원 공간을 다 만들 수 있는 것과 동일합니다. 하지만 2차원과 마찬가지로 예외가 존재하는데, 만약 세 번째 벡터가 두 개의 벡터가 만드는 스팬(평면)에 놓여있다면 세 번째 벡터를 추가해도 스팬이 바뀌지 않습니다. 이를 선형종속이라 하였습니다.