1. 시간 복잡도
1.1 분석 종류
- $T(n)$: Every-case analysis
- 입력크기(input size)에만 종속
- 입력값과는 무관하게 결과값은 항상 일정
- $W(n)$: Worst-case analysis
- 입력크기와 입력값 모두에 종속
- 단위연산이 수행되는 횟수가 최대인 경우 선택
- $A(n)$: Average-case analysis
- 입력크기와 입력값 모두에 종속
- 모든 입력에 대해 단위연산이 수행되는 기대치(평균)
- 각 입력에 대해서 확률 할당 가능
- $B(n)$: Best-case analysis
- 입력크기와 입력값 모두에 종속
- 단위연산이 수행되는 횟수가 최소인 경우 선택
1.2 시간 복잡도 정의
- Big-O
모든 $n$, $n \geq n_0$에 대해 $f(n) \le c\times g(n)$인 조건을 만족시키는 두 양의 상수 $c$와 $n_0$가 존재하기만 하면 $f(n)=O(g(n))$이다.
예를 들면 $O(n)$: 최악의 경우 $n$번까지 수행되면 프로그램을 끝낼 수 있다.
- Big-Omega
모든 $n$, $n \geq n_0$에 대해 $f(n) \geq c\times g(n)$인 조건을 만족시키는 두 양의 상수 $c$와 $n_0$가 존재하기만 하면 $f(n)=\Omega(g(n))$이다.
예를 들면 $O(n)$: 최소 $n$번은 수행되어야 프로그램을 끝낼 수 있다.
- Theta
모든 $n$, $n \geq n_0$에 대해 $c_1\times g(n) \le f(n) \le c_2\times g(n)$인 조건을 만족시키는 세 양의 상수 $c_1, c_2, n_0$가 존재하기만 하면 $f(n)=\theta(g(n))$이다.
Theta의 경우 $O와\ \Omega$의 교집합이다. 즉, 차수가 같은 문제이다.
- Small-O
모든 $n$, $n \geq n_0$에 대해 $0 \leq f(n) \lt c \times g(n)$인 조건을 만족시키는 두 양의 상수 $c, n_0$가 존재하기만 하면 $f(n)=O(g(n))$이다.
예를 들면 $O(n)$: 최악의 경우에도 n번 미만으로 수행되면 프로그램은 끝낼 수 있다.
$\lim_{x \to \infty}$ $f(x)\over g(x)$ $=0$로 나타낼 수 있다.
Small-O와 Big-O의 차이점은 다음과 같다.
- Big-O는 실수 $c>0$ 중에서 하나만 성립해도 된다.
- Small-O는 모든 실수 $c>0$에 대해서 성립해야 한다.
- Small-O는 Big-O에서 등호를 뺀다.
추가적으로 Small-omega($\omega$)도 존재한다.
1.3 시간복잡도 정의를 이용하여 다음 4개의 문제에 대하 statement의 참, 거짓을 판별하시오 (시간복잡도 계산 문제)
1.4 $8n^2 + \sqrt2 = O(n^2)$임을 보여라.
모든 $n, n \geq n_0$에 대하여 $f(n) \leq c \times g(n)$인 조건을 만족시키는 두 양의 상수 $c$와 $n_0$가 존재하기만하면 $f(n) = O(g(n))$이다.
1. $f(n) = 8n^2 + \sqrt2$
2. $g(n) = n^2$
3. 대입 => $8n^2 + \sqrt2 \leq c \times n^2$
4. $\sqrt2$는 약 1.414
5. $8n^2 + 1.414 \leq c \times n^2$
6. n = 2라 가정하면
7. $32 + 1.414 \leq c \times 4$
8. $33.414 \leq c \times 4$
9. $c \geq 9$
1.5 Big-O, Omega, Theta, small-o의 정의를 이용하여 $5x^3 + 4x^2 + 6x \in \Theta(n^3)$ 임을 보이시오.
1. $g(x) = x^3$
2. $g_2(x) = 6x^3$
3. $x^3 \leq 5x^3+4x^2+6x \leq 6x^3$
2. 프림, 크루스칼, 다익스트라
2.1 비방향 그래프를 보고 크루스칼 알고리즘을 이용하여 최소 비용 신장 트리를 구하는 과정을 단계별로 보이시오
- 크루스칼 알고리즘의 핵심
- 오름차순
- 가중치를 기준으로 간선을 오름차순 정렬
- 낮은 가중치의 간선부터 시작해서 하나씩 그래프에 추가
- 사이클을 형성하는 간선을 추가하지 않음
- 간선의 수가 정점의 수보다 하나 적을 때 MST가 완성
- 내림차순
- 가중치를 기준으로 간선을 내림차순으로 정렬
- 높은 가중치의 간선부터 시작해서 하나씩 그래프에서 제거
- 두 정점을 연결하는 다른 경로가 없을 경우 해당 간선은 제거하지 않음
- 간선의 수가 정점의 수보다 하나 적을 때 MST가 완성
- 오름차순
2.2 그래프를 보고 다익스트라 알고리즘을 이용하여 v6를 출발점으로하는 최단 거리를 구하는 과정을 단계별로 보이시오
- 간선의 가중치를 오름차순으로 정렬한다.
- 가중치가 낮은 순서대로 간선을 하나씩 그래프에 추가한다.
- 그래프 내에서 사이클을 형성하는 간선은 추가하지 않는다.
- 간선의 개수가 정점의 개수보다 '1' 작으면 끝낸다.
3. NP, NP-complete
3.1 NP, NP-hard, NP-complete의 정의
- $P$ : 어떤 문제가 주어졌을 때 다항식으로 표현되어 polynomical time 즉, 다항 시간내에 해결 가능한 알고리즘을 의미하며 알고리즘의 복잡도가 $O(n^k)$로 표현되는 문제를 '$P$'라 한다. (복잡도 $O(n^k)$ 이하를 가지는 경우 같은 복잡도 내에 모든 해를 구한다.)
- $NP$ : 어떤 문제가 주어졌을 때 다항식으로 표현될 수 있는지의 여부가 결정되지 않은 문제들을 'NP(Non-deterministic polynomial)'라 한다.
- $NP-Complete$ : NP이면서 동시에 NP-Hard 에 속한다면 그 문제는 'NP-Complete'라 한다. (전수조사가 답)
- $NP-Hard$ : 적어도 모든 NP 문제만큼은 어려운 문제들의 집합이며, 만약 P-NP 문제가 P=NP로 풀린다면 P=NP=NP-Complete이므로 P와 NP는 NP-Hard의 부분집합이 되고, P≠NP인 경우는 P와 NP-Hard는 서로소가 된다. *다항시간 : $T(n) = O(n^k), k$ 는 상수 => $k$가 상수로 고정이 된다면 그 문제는 해결하기 쉬운 문제. 다항시간안에 풀 수 있는 문제이므로.
3.2 해밀턴회로 거리 구하기(그래프가 주어질 때 그래프의 모든 점을 정확하게 한번씩만 지나는 경로가 존재하는가?) (NP-hard)
4. 배열 제시 후 소팅 알고리즘을 사용하여 정렬 과정을 보여라
4.1 Merge sort 알고리즘을 사용하여 8개의 숫자를 정렬하는 과정을 보여라
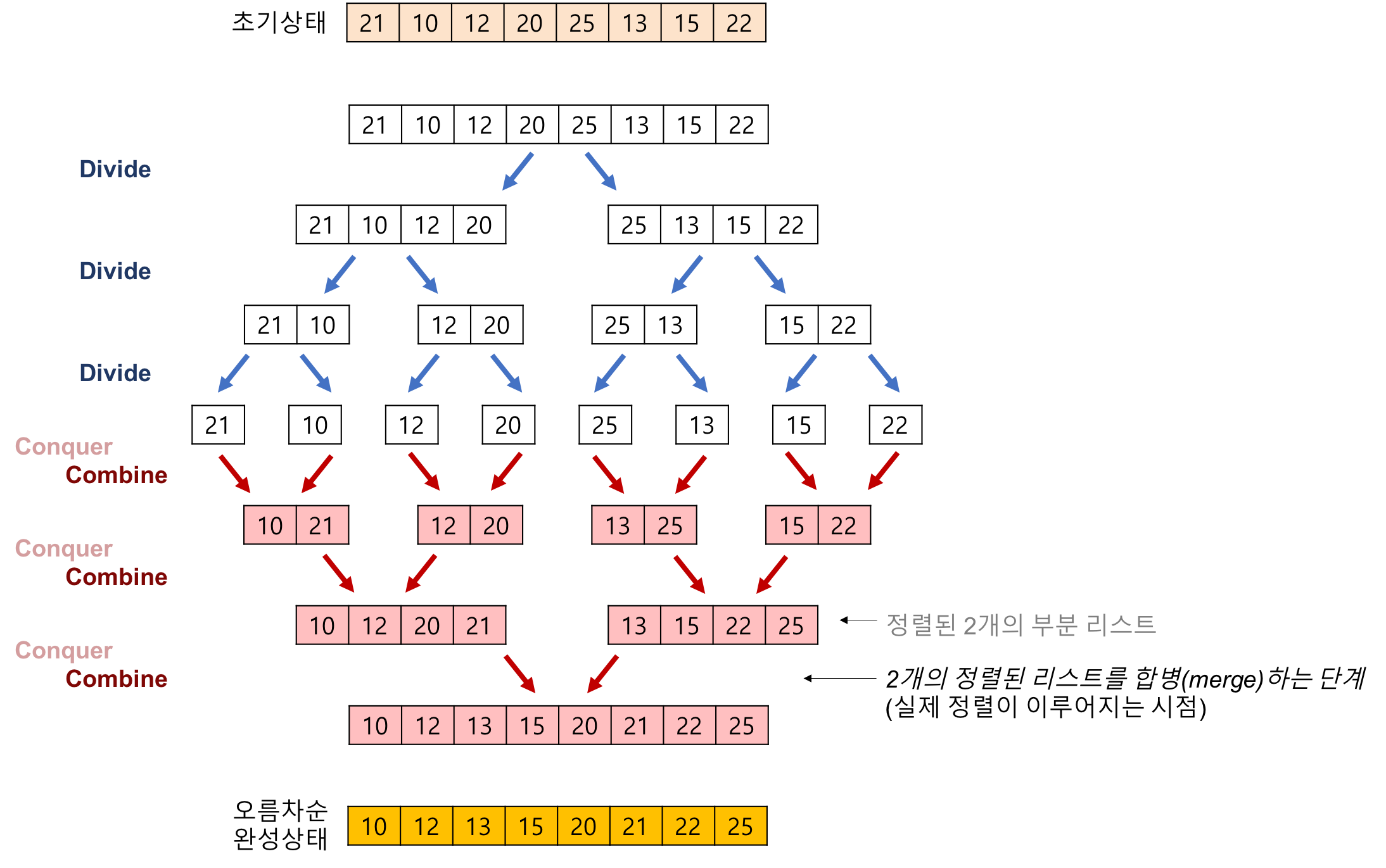
4.2 각종 정렬 기법들의 장단점과 시간복잡도
5. Divide and Conquer 알고리즘과 Dynamic Programming 알고리즘 차이
5.1 분할 정복법이 비효율적인 경우를 설명하라
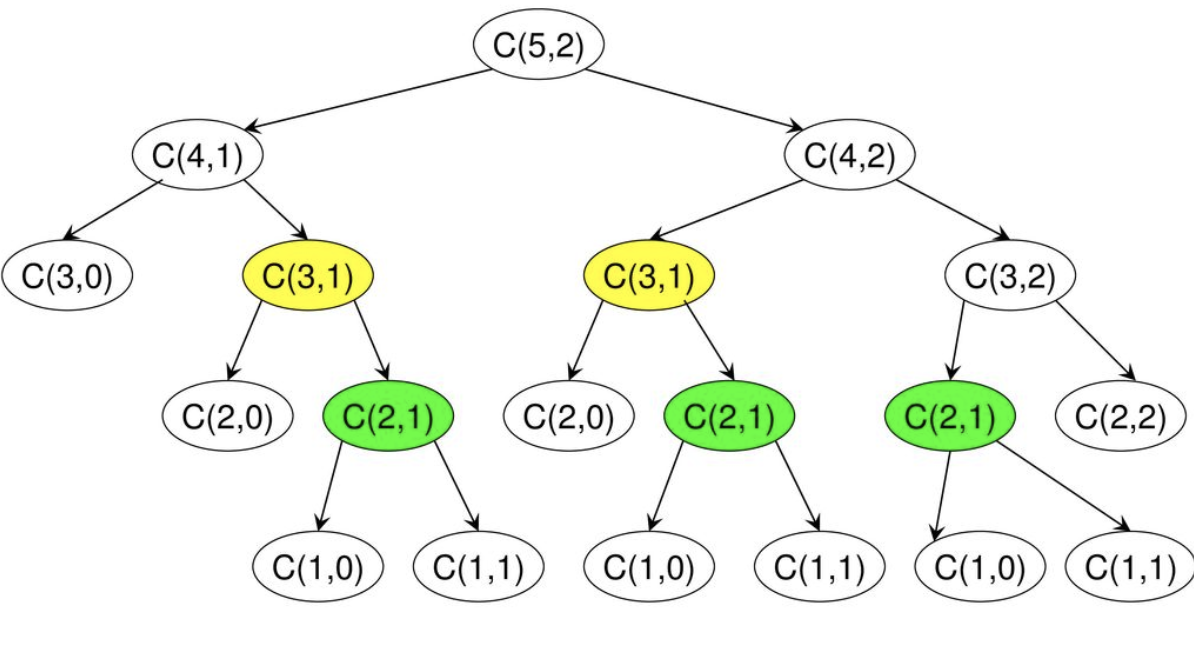
5.2 분할 정복법과 동적프로그래밍을 이용하여 이항계수를 구하는 알고리즘 작성 후 두방식의 차이점에 대해 적으시오
- 분할 정복법(Divide and Conquer)
- 어떠한 큰 문제를 해결하기 위해 큰 문제를 작은 단위의 문제로 나누어 해결하는 방법 (Top-down)
- 문제의 크기가 충분히 작아질때까지 반복적으로 분할
- 해결한 작은 문제를 가지고 바로 윗 단계의 문제를 해결해 나가는 방식
- 대표적인 예로는 Binary Search와 Merge Sort, Quick Sort 등이 있다.
- 동적 프로그래밍(Dynamic Programming)
- 문제를 작은 인스턴스들로 나누고 Bottom-up 순서로 풀어나가면서 문제의 값을 정해놓고 필요할 때 가져와 문제를 해결하는 방식이다. "기억하며 풀기"라 생각하면 된다.
- 대표적인 예로는 TSP 문제, 피보나치 수열, 파스칼의 트리 작성 등이 있다.
분할정복법과 동적 프로그래밍의 공통점과 차이점
- 공통점 : 문제를 작은 단위로 나누어 해결
- 차이점 : 분할정복법은 Top-down 방식이며, 동적 프로그래밍은 Bottom-up 방식이다.
5.3 Binomial coefficient를 계산하려할 때 다음을 구해라
- Divide-and-Conquer 방법을 사용하는 pseudo code 작성
- Dynamic Programming 방법을 사용하는 pseudo code 작성
- 위 두 접근 방법의 차이점을 서술
5.4 이항계수 수학적 귀납법으로 증명하고, 동적 프로그래밍으로 알고리즘을 구현하라.
bottom-up 방식
int binomial(int n, int k)
{
for (int i=0; i<=n; i++)
{
for (int j=0; j<=k && j<=i; j++)
{
if (k==0 || n==k)
arr[i][j] = 1;
else
arr[i][j] = arr[i-1][j-1] + arr[i-1][j];
}
}
return arr[n][k];
}
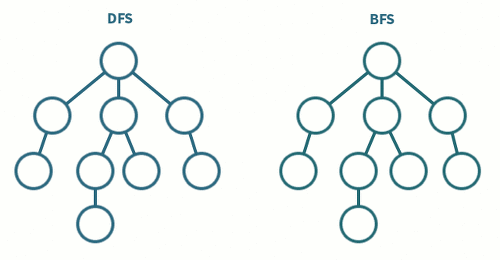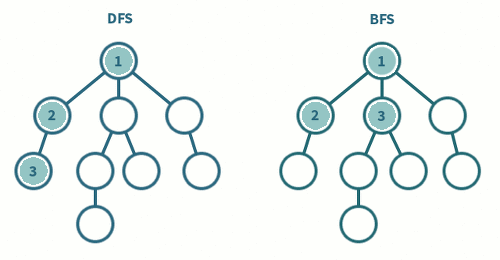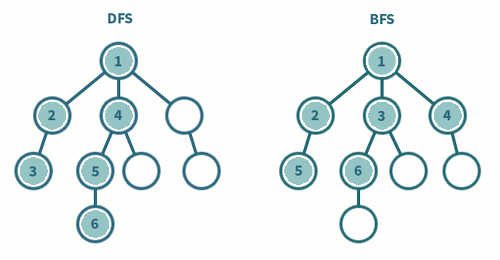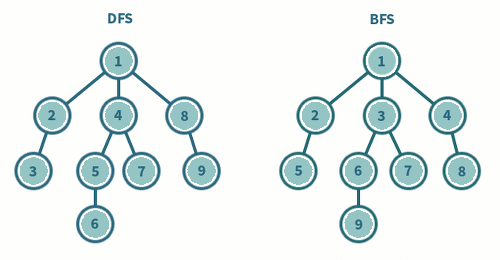
6. DFS(Depth First Search)와 BFS(Breadth First Search)의 차이
- DFS, BFS의 의사코드를 작성하고 이들의 차이를 제시한 다음, 간단한 트리를 작성하여 순회하는 것을 보이시오.
8. 행렬을 주고 TSP에 관한 문제
9. Strassen 행렬 알고리즘을 사용하여 2*2 행렬 A,B의 곱 C를 구하라(m1,m2,...,m7)을 사용해야함
9.1 Strassen's Matrix Multiplication 알고리즘에 대해 설명하라
9.2 행렬 곱셉 알고리즘 + 쉬트라센 + 복잡도
아래와 같이 행렬 A,B가 있고 두 행렬의 곱이 행렬 C로 표현한다 가정한다.
$A = \left[ \begin{array}{cc|c} a_{11} & a_{12} \\\\ a_{21} & a_{22} \end{array} \right],\ $ $B= \left[ \begin{array}{cc|c} b_{11} & b_{12} \\\\ b_{21} & b_{22} \end{array} \right],\ $ $C=\left[ \begin{array}{cc|c} c_{11} & c_{12} \\\\ c_{21} & c_{22} \end{array} \right]$
이 때, $A_{ij},B_{ij},C_{ij} \in F^{2^n-1 \times 2^n-1}$ 이다.
따라서 일반적인 행렬의 곱은 다음과 같이 표현할 수 있으며, 총 8번의 곱셈과 4번의 덧셈으로 연산된다.
$C_{11} = A_{11}B_{11} + A_{12}B_{21}$
$C_{12} = A_{11}B_{12} + A_{12}B_{22}$
$C_{21} = A_{21}B_{11} + A_{22}B_{21}$
$C_{22} = A_{21}B_{12} + A_{22}B_{22}$
슈트라센 알고리즘은 행렬의 곱셉을 더하기 연산으로 풀어 각 원소를 구할 수 있는 $M$이라는 연산 행렬로 표현한다. 행렬 $M$은 7번의 곱셈과 10번의 덧셈으로 연산으로 나타낼 수 있으며 아래와 같이 표현한다.
$M_1 = (A_{11} + A_{22})(B_{11}+B_{22})$
$M_2 = (A_{21} + A_{22})B_{11}$
$M_3 = A_{11} (B_{12}-B_{22})$
$M_4 = A_{22}(B_{21}-B_{11})$
$M_5 = (A_{11} + A_{12})B_{22}$
$M_6 = (A_{21} - A_{11})(B_{11}+B_{12})$
$M_7 = (A_{12} - A_{22})(B_{21}+B_{22})$
최종적으로 행렬 C는 행렬 M의 더하기 연산으로 이루어져 있으며 각 원소에 해당하는 방법은 다음과 같다.
$C_{11} = M_1 + M_4 - M_5 + M_7$
$C_{12} = M_3 + M_5$
$C_{21} = M_2 + M_4$
$C_{22} = M_1 - M_2 + M_3 + M_6$
10. 5-Queen 문제를 백트래킹과 상태 설명 트리를 사용하여 해결하라
11. Floyd 알고리즘을 사용하여 W(=D0) 행렬과 D(=D) 행렬을 구하라. W, D를 구하는 과정을 서술하라
11.1 방향 그래프를 보고 플로이드 알고리즘을 이용하여 D와 P를 단계별로 적으시오.
12. 하노이의 탑 알고리즘을 써라
#include <stdio.h>
void HanoiTowerMove(int num, char from, char by, char to)
{
if (num == 1)
printf("원반 1을 %c에서 %c로 이동 \n", from, to);
else
{
HanoiTowerMove(num - 1, from, to, by);
printf("원반 %d를 %c에서 %c로 이동 \n", num, from, to);
HanoiTowerMove(num - 1, by, from, to);
}
}
int main(void)
{
// 막대 A의 원반 5개를 막대 B를 경유하여 막대 C로 옮기기
HanoiTowerMove(5, 'A', 'B', 'C');
return 0;
}
13. 탐욕적 방법 Greedy Algorithm이 항상 최적의 해를 내지 못하는 경우의 예를 들라
Greedy Algorithm이 사용되는 대표적인 예제로는 "최소 수의 동전으로 거스름돈 거슬러주기" 문제가 있다.
만약 우리가 마트의 캐셔로 일을 하고 있고, 850원을 거슬러 주어야 할 때 500원 동전 1개와 100원 동전 3개와 50원 동전 1개 총 4개의 동전을 건넴으로써 최소한의 동전을 거슬러 줄 수 있다. 하지만 이렇게 하지 않고 10원짜리 동전 85개를 건네주거나 50원짜리 17개를 건네주는 방법과 같이 다양한 경우의 수가 존재하며 이와 같을 경우 반드시 최적의 해를 내는 것은 아니다.
또한 우리나라의 경우 총 4개의 동전 500원, 100원, 50원, 10원이 있다. 하지만 만약 400원 동전이 발행된다면 400원 동전 2개, 50원 동전 1개를 통해 총 3개의 동전을 거슬러 줄 수 있을 것이다. 가장 최적의 방법이지만, 기존 알고리즘에 따르면 500원 1개, 100원 3개, 50원 1개로 거슬러주게 될 것이다. 이와 같이 탐욕 알고리즘은 항상 최적의 결과를 보장하지 못한다.
Reference
[1] https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
[2] https://janghw.tistory.com/entry/알고리즘-Greedy-Algorithm-탐욕-알고리즘
'Computer Science > 백준 알고리즘' 카테고리의 다른 글
| [백준 알고리즘] 2908번 상수 (C++) (0) | 2021.11.01 |
|---|---|
| [알고리즘] N 계단 오르기 (0) | 2021.10.20 |
| 쉬트라센 알고리즘 (Strassen Algorithm) (0) | 2020.03.04 |
| 분할정복법과 동적프로그래밍 (0) | 2020.03.04 |
| 정렬 알고리즘의 장단점과 시간 복잡도 및 공간 복잡도 (2) | 2020.03.04 |
