이진 탐색 알고리즘은 탐색 알고리즘 종류 중 하나로, 이름 그대로 절반씩 나누어 원하는 값을 알고리즘이다. 이진 탐색을 위한 전제 조건으로 배열이 오름차순 또는 내림차순으로 정렬되어 있어야 한다. 동작 방식은 간단하다. 배열의 중앙을 기준으로 원하는 값이 작은지 큰지 비교하여 한 쪽을 배제하고 나머지 부분을 반복해서 탐색하는 방식이다.
가령 예를 들어 아래와 같이 찾고자 하는 값이 5일 경우, 배열의 가운데인 4를 기준으로 삼은 다음 오른쪽에 있다는 것을 알 수 있다. 이후 왼쪽 배열 0~4를 배제하고 오른쪽 배열 5~9 부분을 탐색한다. 찾고자 하는 값이 5~9 부분의 중앙인 7을 기준으로 왼쪽에 있으므로 다시 오른쪽 배열을 배제하고 왼쪽 배열 5~7을 탐색한다. 6을 기준으로 왼쪽에 있으므로 오른쪽 7을 배제하고 왼쪽 5를 찾으며 탐색이 완료되는 방식으로 동작한다.
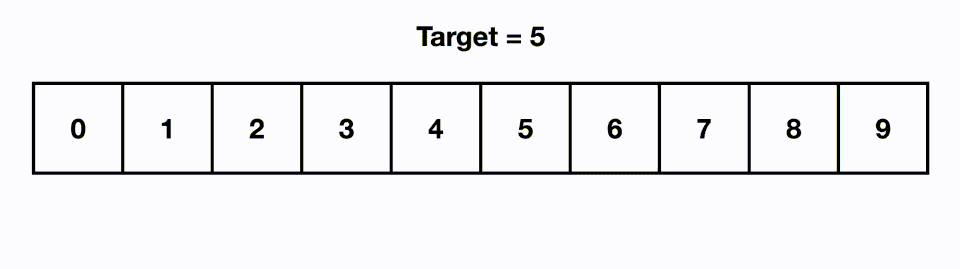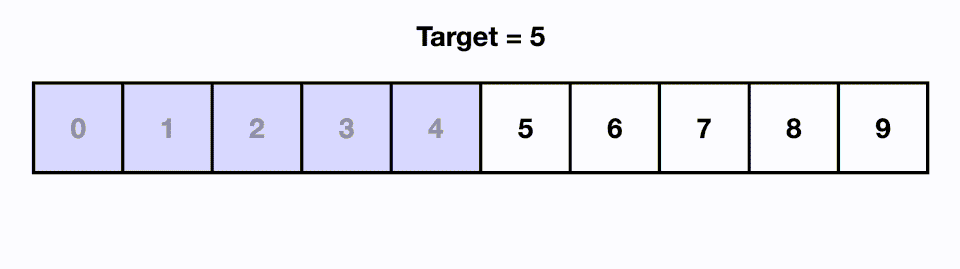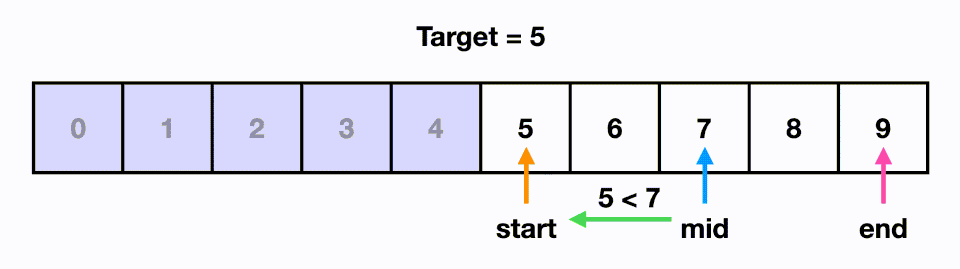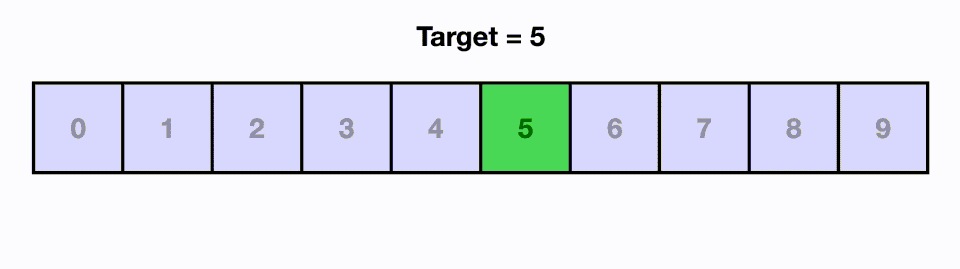
원하는 값을 찾기 위해 배열의 모든 원소를 탐색하는 순차 탐색의 경우 시간복잡도가 $O(n)$이다. 하지만 이진 탐색의 경우 시간복잡도가 이보다 작은 $O(logN)$이 된다는 것이 특징이다. 조금 덧붙이자면 시간복잡도 $O(logN)$는 배열이 정렬되고 고정된 상태에서 가능하다. 만약 배열에 삽입, 제거, 탐색과 같은 연산이 함께 이뤄진다면 시간복잡도가 $O(n)$까지 떨어질 수 있다. 때문에 삽입, 제거, 탐색과 같은 연산이 함께 이뤄지는 경우 이진탐색 트리를 자료구조로서 사용해야 한다. 이진탐색트리의 경우 삽입, 제거, 탐색을 해도 시간복잡도가 $O(logN)$이 보장되는 특징이 있기 때문이다.
이진 탐색 알고리즘 구현은 크게 두 가지 방법이 있다. 첫 번째는 재귀를 사용하지 않는 방식이고, 두 번째는 재귀를 사용하는 방식이다. 두 구현 방법 모두 공통적으로 세 종류의 변수들이 필요하다.
1. 정렬된 배열 (array)
2. 찾고자 하는 값 (target)
3. 배열의 인덱스 표시 (start, end, mid)
이진 탐색 비재귀적 구현
array = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
start, end = 0, len(array)-1
target = 5
while start <= end:
mid = (start + end) // 2
if array[mid] == target:
return mid
elif array[mid] < target:
start = mid + 1
elif array[mid] > target:
end = mid - 1
이진 탐색 재귀적 구현
def binary_search(array, start, end, target):
if start > end:
return None
mid = (start + end) // 2
if array[mid] == target:
return mid
elif array[mid] < target:
start = mid + 1
elif array[mid] > target:
end = mid - 1
return binary_search(array, start, end, target)
if __name__ == "__main__":
target = 5
array = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
start, end = 0, len(array)-1
index = binary_search(array, start, end, target)
print (index)
만약 결과가 출력되지 않을 경우 주어진 배열안에 target이 없는 것임.
Reference
[1] GIF of binary search: https://stackoverflow.com/questions/70131709/python-binary-search-mid-calculation
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 최소 신장 트리와 크루스칼 알고리즘 (0) | 2022.10.06 |
|---|---|
| [자료 구조] 최단 거리 알고리즘 정리 (다익스트라, 벨만 포드, 플로이드 워셜) (5) | 2022.09.20 |
| [자료구조] 링크드 리스트 (Linked List) (1) | 2022.09.05 |
| [자료구조] 기본 정렬 알고리즘 총 정리 (4) | 2022.08.13 |