최소 신장 트리란?
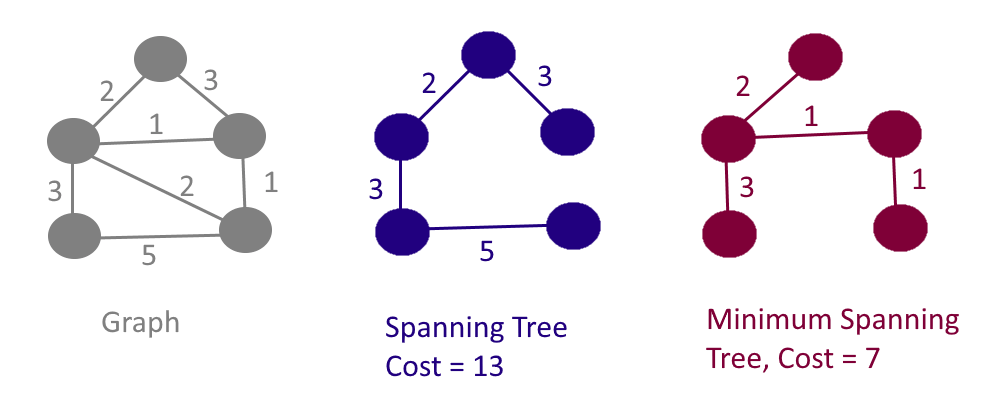
신장 트리란 그래프 상에서 모든 노드가 사이클 없이 연결된 부분 그래프를 뜻한다. 이 부분 그래프는 여러개가 존재할 수 있다. 따라서 최소 신장 트리란 여러 개의 부분 그래프 중 모든 정점이 최소 간선의 합으로 연결된 부분 그래프이다.
(* 트리와 그래프 관계: 트리는 그래프 중에서 특수한 경우에 해당하는 자료구조로, 사이클이 존재하지 않는 방향 그래프다)
최소 신장 트리의 활용
이런 최소 신장 트리는 실생활 곳곳에 활용된다. 예를 들어 도로 건설 문제에서 도시를 노드, 도로를 간선으로 두고 도시 간 이어지는 도로 길이를 최소화 할 때 사용된다. 또 네트워크에서 최적의 라우팅 경로를 선택할 때도 사용되며, 통신에서도 전화선 길이가 최소가 되는 케이블망 구축에 사용되는 등 여러 곳에서 활용된다.
최소 신장 트리 알고리즘
최소 신장 트리를 찾을 수 있는 알고리즘은 크게 2가지로 크루스칼(Kruscal), 프림(Prim) 알고리즘이 있다. 두 알고리즘 간 차이점은 크루스칼은 간선 중심이고 프림은 정점 중심 알고리즘이다. 간선이 적으면 크루스칼을, 간선이 많으면 프림을 사용하는 것이 좋다. 알고리즘 시간 복잡도는 크루스칼이 $O(E+\log (E))$, 프림이 $O(V+E) \log (V)$이다. 두 알고리즘의 공통점 중 하나는 음수 사이클이 있더라도 최소 신장 트리를 구할 수 있다. 본 포스팅에서는 크루스칼 알고리즘만 다룬다.
크루스칼 알고리즘 (Kruscal Algorithm)
크루스칼 알고리즘은 음의 가중치가 없는 무방향 그래프에서 최소 신장 트리를 찾는 알고리즘이다. 최소 신장 트리를 찾기 위해선 사이클 발생 여부를 판단할 수 있어야 한다. 사이클 발생 여부는 union find 알고리즘을 사용해서 판단한다. union find를 알면 크루스칼 알고리즘 이해에 도움되지만 모르더라도 아래 설명을 통해 어느정도 이해 가능할 것이다.
크루스칼 알고리즘은 크게 아래 3단계로 구성되며 2~3이 반복 수행된다.
1. 주어진 모든 간선을 오름차순 정렬 수행한다.
2. 정렬된 간선을 하나씩 확인하며 현재 간선이 노드 간 사이클을 발생시키는지 확인한다.
3. 사이클 발생시키지 않을 경우 최소신장트리에 포함, 사이클 발생할 경우 포함하지 않는다.
도식화 한 예시로 확인해보자. 예를 위해 아래와 같이 노드 6개와 간선 8개로 구성된 그래프가 있다 가정하자.

위 그림에서 간선의 비용 별로 오름차순 정렬해 주었다. 또 내부적으로 사이클 여부를 판별하기 위해 union-find 알고리즘을 사용하므로 부모 테이블을 만들어주고 초기값은 노드 자기자신으로 둔다. 이제 간선을 비용이 작은 순서대로 확인하기 위해 먼저 간선 (3,6)을 살펴보자.
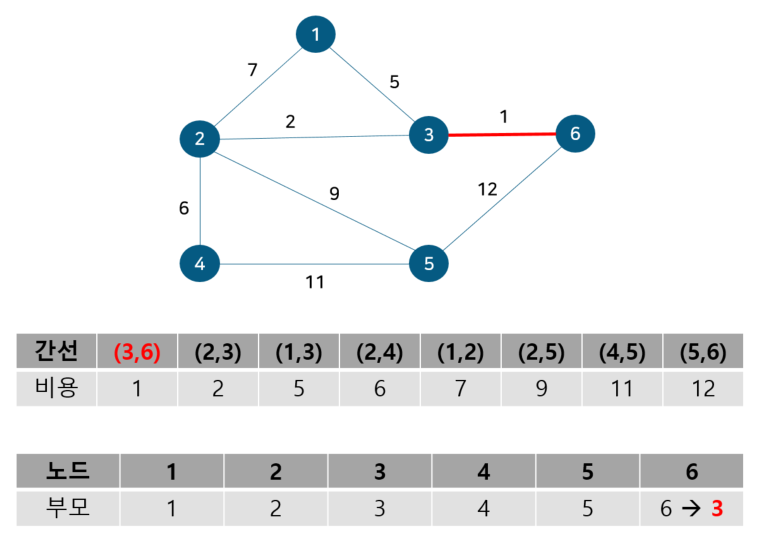
노드 3, 6의 부모 노드를 살펴보면 각각 3, 6으로 다르기에 사이클이 발생하지 않는다. 따라서 최소 신장 트리에 (3, 6)을 포함시키고 부모 테이블에서 노드 6의 부모를 노드 3으로 업데이트 해준다. 참고로 일반적으로 부모 노드는 작은 노드 번호 기준으로 업데이트한다. 다음으로 노드 2, 3을 살펴보자

노드 2, 3의 부모 노드를 살펴보면 각각 2, 3으로 다르기에 사이클이 발생하지 않는다. 따라서 최소 신장 트리에 (2, 3)을 포함시키고 부모 테이블에서 노드 3의 부모를 노드 2로 업데이트 해준다. 이 때 노드 6도 부모 노드를 3으로 가지는 종속 관계에 있으므로 함께 바꿔준다. 다음으로 노드 1, 3을 살펴보자
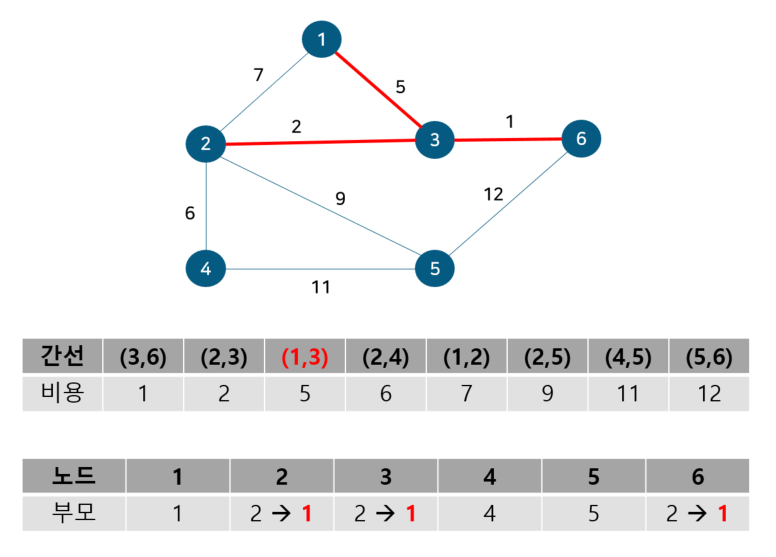
노드 1, 3의 부모 노드를 살펴보면 각각 1, 2로 다르기에 사이클이 발생하지 않는다. 따라서 최소 신장 트리에 (1, 3)을 포함시키고 부모 테이블에서 노드 3의 부모를 노드 1로 업데이트 해준다. 이 때 노드 2, 6도 부모 노드를 2로 가지는 종속 관계에 있으므로 함께 바꿔준다. 다음으로 노드 2, 4를 살펴보자

노드 2, 4의 부모 노드를 살펴보면 각각 1, 4로 다르기에 사이클이 발생하지 않는다. 따라서 최소 신장 트리에 (2, 4)를 포함시키고 부모 테이블에서 노드 4의 부모를 노드 1로 업데이트 해준다. 다음으로 노드 1, 2를 살펴보자
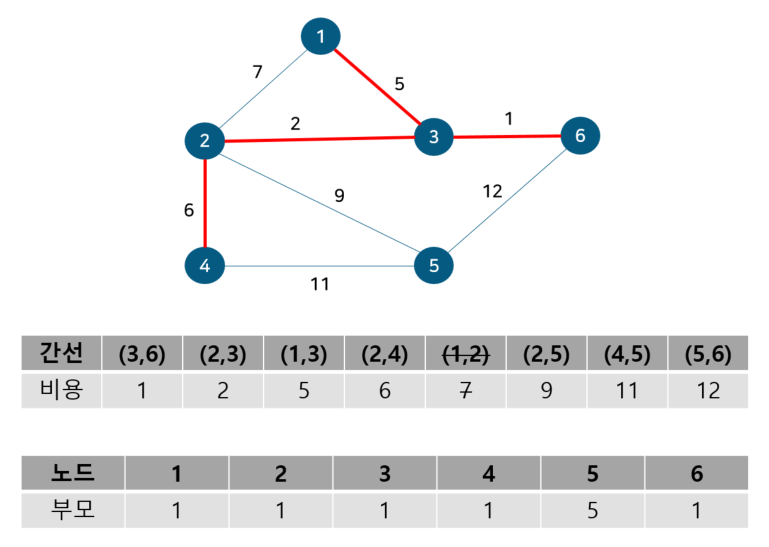
노드 1, 2의 부모 노드를 살펴보면 각각 1, 1로 같아 사이클이 발생했다. 그러므로 최소 신장 트리에 포함시키지 않고, 부모 테이블 업데이트도 이뤄지지 않는다. 다음으로 노드 2, 5를 살펴보자

노드 2, 5의 부모 노드를 살펴보면 각각 1, 5로 다르기에 사이클이 발생하지 않는다. 따라서 최소 신장 트리에 (2, 5)를 포함시키고 부모 테이블에서 노드 5의 부모를 노드 1로 업데이트 해준다. 다음으로 노드 4, 5를 살펴보자

노드 4, 5의 부모 노드를 살펴보면 각각 1, 1로 같아 사이클이 발생했다. 그러므로 최소 신장 트리에 포함시키지 않고, 부모 테이블 업데이트도 이뤄지지 않는다. 다음으로 노드 5, 6를 살펴보자

노드 5, 6의 부모 노드를 살펴보면 각각 1, 1로 같아 사이클이 발생했다. 그러므로 최소 신장 트리에 포함시키지 않고, 부모 테이블 업데이트도 이뤄지지 않는다. 이것으로 최소 신장 트리를 찾는 크루스칼 알고리즘 동작이 종료된다. 동작 전과 동작 후를 비교해보자면 다음과 같다.

기존의 그래프 전체에서 사이클 없이 모든 정점을 최소 비용 간선으로 잇는 부분 그래프인 최소 신장 트리다. 이를 코드로 구현하면 다음과 같다.
""" This is input value. you can just copy and past it.
then you can get "[(3, 6), (2, 3), (1, 3), (2, 4), (2, 5)]" and "23"
6 8
1 2 7
1 3 5
2 3 2
2 4 6
2 5 9
3 6 1
4 5 11
5 6 12
"""
import sys
input = sys.stdin.readline
def find_parent(parent, x):
""" 부모 노드를 찾기 위해 재귀 수행"""
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent, a, b):
""" 부모 노드 비교 후 부모 노드 업데이트 """
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
if __name__ == "__main__":
V, E = map(int, input().split()) # make graph
graph = []
for _ in range(E):
a, b, cost = map(int, input().split())
graph.append([a, b, cost])
graph.sort(key=lambda x:x[2])
parent = [0] * (V+1) # make parent table
for i in range(1, V+1):
parent[i] = i
costs, mst = 0, [] # get mst
for i in range(E):
a, b, cost = graph[i]
if find_parent(parent, a) != find_parent(parent, b): # check cycle
union_parent(parent, a, b)
mst.append((a, b))
costs += cost
print (mst)
print (costs)
이 알고리즘을 그대로 활용하여 백준 1197 최소 스패닝 트리 문제를 해결할 수 있다.
이 알고리즘을 조금만 활용하여 백준 1647 도시 분할 계획 문제를 해결할 수 있다.
Reference
[1] https://algorithms.tutorialhorizon.com/introduction-to-minimum-spanning-tree-mst/
[2] https://techblog-history-younghunjo1.tistory.com/262
[3] http://blog.skby.net/최소-신장-트리-mst-minimal-spanning-tree/
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료 구조] 최단 거리 알고리즘 정리 (다익스트라, 벨만 포드, 플로이드 워셜) (5) | 2022.09.20 |
|---|---|
| [자료구조] 링크드 리스트 (Linked List) (1) | 2022.09.05 |
| [자료구조] 이진 탐색 알고리즘 (Binary Search Algorithm) (0) | 2022.08.22 |
| [자료구조] 기본 정렬 알고리즘 총 정리 (4) | 2022.08.13 |