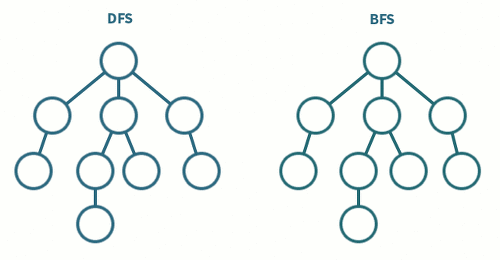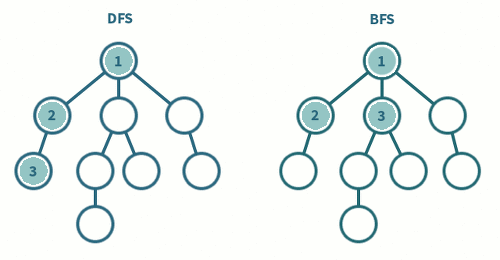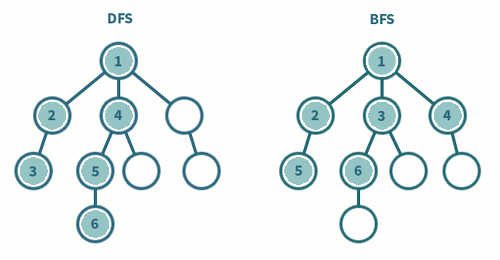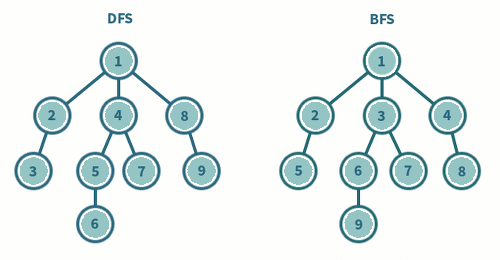
최단 거리 알고리즘이란 그래프 상에서 노드 간의 탐색 비용을 최소화하는 알고리즘이다. 일반적으로 네비게이션과 같은 길찾기에 적용된다. 최단 거리 알고리즘 종류는 크게 3가지가 있다. 1. 다익스트라(Dijkstra) 2. 플로이드 워셜(Floyd Warshall) 3. 벨만 포드(Bellman Ford)이다.
1. 다익스트라 (Dijkstra) 알고리즘
다익스트라 알고리즘은 그래프 상에서 특정 한 노드에서 다른 모든 노드까지의 최단거리를 구하는 알고리즘이다. 다르게 표현하면 가중 그래프에서 간선 가중치의 합이 최소가 되는 경로를 찾는 알고리즘 중 하나이다.
다익스트라는 그리디와 동적 계획법이 합쳐진 형태이다. 현재 위치한 노드에서 최선의 경로를 반복적으로 찾으면서도 계산 해둔 경로를 활용해 중복된 하위 문제를 풀기 때문이다. 다익스트라는 만약 그래프에 음의 가중치가 있다면 사용할 수 없다. 그 이유는 그리디를 통해 최단 경로라고 여겨진 경로 비용을 DP 테이블에 저장한 뒤, 재방문하지 않는데, 만약 음의 가중치가 있다면 이러한 규칙이 어긋날 수 있기 때문이다. 음의 가중치가 포함된다면 플로이드 워셜이나 벨만 포드 알고리즘을 사용해 최단 경로를 구할 수 있다. 다만 시간 복잡도가 늘어나는 단점이 있기에 해결하고자 하는 문제에 맞게 사용해야 한다.
만약 아래와 같은 그래프가 있다 가정하고 동작 원리를 확인해보자.
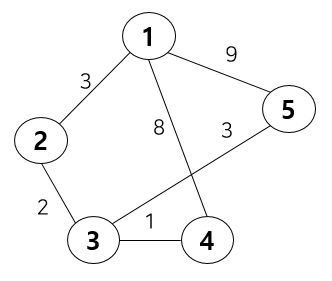
위와 같은 초기 노드와 간선을 테이블에 나타내보자면 다음과 같다. 예를 들자면 1행 4열은 1번 노드에서 4번 노드로 가는 것을 나타내며 비용은 8이 든다.
| 0 | 3 | INF | 8 | 9 |
| 3 | 0 | 2 | INF | INF |
| INF | 2 | 0 | 1 | 3 |
| 8 | INF | 1 | 0 | INF |
| 9 | INF | 3 | INF | 0 |
다익스트라 알고리즘은 특정 한 노드에서 다른 모든 노드까지의 최단 거리를 구하는 알고리즘이라 했다. 예를 들어 특정 한 노드를 1이라 가정하면 [0, 3, INF, 8, 9]는 다음과 같은 과정을 통해 업데이트 된다.
아래와 같이 노드 1을 선택하게 되면 1과 연결된 3개의 간선을 확인한다.
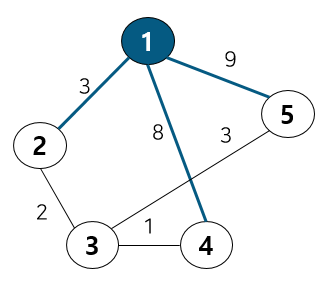
이 중에서 다른 정점으로 가는 최소 비용이 2번 노드가 가장 작기 때문에 2번 노드로 이동하고, 노드 1번은 방문 처리한다. 이 때 테이블 값 변화는 없다.
| 0 | 3 | INF | 8 | 9 |

2번 노드에 연결된 노드는 1번과 3번이다. 하지만 1번의 경우 이미 방문했고, 비용이 크므로 볼 필요 없다. 2와 최소비용으로 연결된 노드는 3이기 때문에 노드 3으로 이동하고, 2를 방문처리 한다. 이 때 테이블 값 변화가 발생한다. 1과 3은 연결되지 않았었다. 하지만 그리디와 같이 계속해서 최적의 상태를 업데이트 하므로 다른 노드를 탐색하다 3을 방문할 수 있기 때문에 1 → 2 → 3으로 이동하는 동안의 비용인 5로 업데이트 해준다.
| 0 | 3 | 5 | 8 | 9 |
다음으로 3번 노드에 연결된 간선은 총 3개이다. 하지만 2의 경우 방문처리 되었으니 노드 4, 5번 두 개만 고려하면 된다.
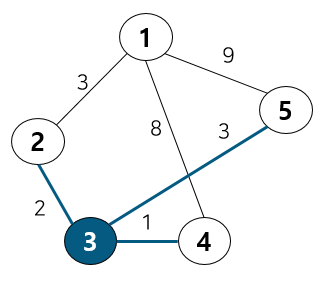
노드 4, 5번 중 더 비용이 적은 것은 4번 노드이므로, 4번 노드로 이동하고 3번 노드는 방문처리 해준다. 마찬가지로 테이블 값 변화가 발생한다. 기존에는 1 → 4로 가는 비용이 8이었지만 1 → 2 → 3 → 4를 거치는 것이 6이 들기에 테이블 값을 6으로 업데이트 시켜준다.
| 0 | 3 | 5 | 6 | 9 |
다음으로 4번 노드에 연결된 간선은 총 2개이다. 하지만 두 개 모두 방문처리 되었고 5로 가는 간선이 없다.
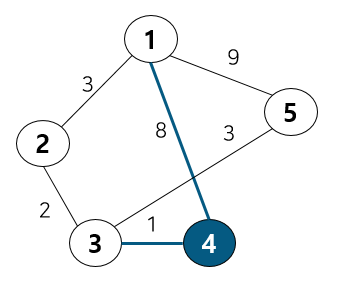
따라서 테이블 값 업데이트는 없다. 또 알고리즘은 여기서 끝이 난다. 최종적으로 1에서 다른 모든 노드까지의 비용은 아래 테이블이 된다.
| 0 | 3 | 5 | 6 | 9 |
이를 코드로 구현하기 위해서는 가중치에 중요도가 있으므로 자료구조 힙을 사용해 표현해준다. 전체 코드는 다음과 같다.
""" This is input value. you can just copy and paste it.
5 6 1
1 2 3
1 4 8
1 5 9
2 1 2
2 3 2
3 2 2
3 4 1
3 5 3
4 1 8
4 3 1
5 1 9
"""
import heapq
def dijkstra(start):
heap = []
heapq.heappush(heap, [0, start]) # 최소힙은 배열의 첫 번째 값을 기준으로 배열을 정렬.
INF = float('inf')
weights = [INF] * (vertex+1) # DP에 활용할 memoization 테이블 생성
weights[start] = 0 # 자기 자신으로 가는 사이클은 없으므로.
while heap:
weight, node = heapq.heappop(heap)
if weight > weights[node]: # 비용 최적화 전부터 큰 비용일 경우 고려할 필요 없음.
continue
for n, w in graph[node]: # 최소 비용을 가진 노드를 그리디하게 방문한 경우 연결된 간선 모두 확인
W = weight + w
if weights[n] > W: # 여러 경로를 방문해 합쳐진 가중치 W가 더 비용이 적다면
weights[n] = W # 업데이트
heapq.heappush(heap, (W, n)) # 최소 비용을 가진 노드와 합쳐진 가중치 추가
return weights
vertex, edge, start = map(int, input().split())
graph = [[] for _ in range(vertex+1)]
for i in range(vertex+edge):
src, dst, weight = map(int, input().split())
graph[src].append([dst, weight])
weights = dijkstra(start)
print (weights) # [inf, 0, 3, 5, 6, 8]
최종 출력되는 최소 비용 중 1에서 1로 가는 사이클은 없으므로 0이 된다. 또한 만약 주어진 문제가 1에서 3으로 가는 최소비용을 구하는 것이라면 5가 되고, 1에서 4로가는 최소 비용을 구하는 것이라면 6이 된다.
참고로 시간 복잡도는 $O((V+E) \log V)$이다.
위와 알고리즘을 동일하게 이용하여 백준 1916번: 최소비용 구하기 문제를 해결할 수 있다.
2. 벨만 포드 (Bellman Ford) 알고리즘
벨만 포드 알고리즘은 가중 유향 그래프 상에서 특정 한 노드로 부터 다른 노드까지의 최단 경로를 구하는 알고리즘이다. 다익스트라 알고리즘의 한계점을 보완하기 위해 나왔다. 그 한계점이란 간선이 음수일 때 최단 경로를 구할 수 없다는 것이다. 사실 정확히는 음의 가중치 자체가 문제가 되진 않는다. 문제는 사이클 형성 여부에 따라 달렸다. 만약 사이클을 형성하면 문제가 된다. 아래 그림을 보자.

만약 다익스트라 알고리즘을 통해 특정 한 노드(1)에서 다른 노드(2)로의 최소 거리를 구하는 문제를 해결하려 한다면 가중치 3 → 4 → 5를 거쳐 비용이 12가 된다. 하지만 중간에 사이클이 있기 때문에 3 → 4 → -6 → 4 → -6 → 4 → -6 ...이 되어 비용이 무한히 작아지게 된다.
이러한 문제점을 해결하기 위해 나온 알고리즘이 벨만 포드이다. 기본적으로 다익스트라와 동일하지만 핵심 차이점은 간선의 가중치가 음일 때도 최소 비용을 구할 수 있다. 다만 시간복잡도가 늘어나기 때문에 가중치가 모두 양수일 경우 다익스트라를 사용하는 것이 좋다. 시간 복잡도가 늘어나는 이유는 그리디하게 최소 비용 경로를 찾아가는 다익스트라와 달리, 벨만 포드는 모든 경우의 수를 고려하는 동적 계획법이 사용되기 때문이다.
그렇다면 모든 경우의 수를 어떻게 고려할까? 그 방법은 매 단계 마다 모든 간선을 전부 확인하는 것이다. 다익스트라는 출발 노드에서만 연결된 노드를 반복적으로 탐색하며 다른 모든 노드까지의 최소 거리를 구했다. 하지만 벨만 포드는 모든 노드가 한번씩 출발점이 되어 다른 노드까지의 최소 비용을 구한다.
아직 조금 추상적이니 구체적인 아래 그림을 보며 동작 과정을 알아보자.
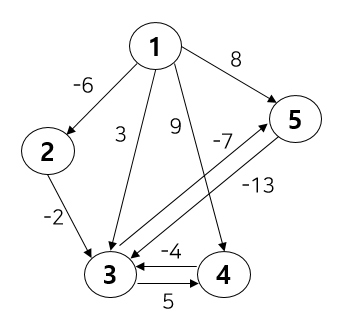
위와 같은 그래프가 있다고 할 때 모든 노드가 한 번씩 출발 노드가 될 것이다. 복잡하지 않다. Itertation 1회, 2회일 때를 이해하면 귀납적으로 적용하여 이해할 수 있기 때문이다.
위와 같은 초기 상태의 그래프가 있을 때, 가중치를 담을 DP 테이블 값은 아래와 같이 모두 INF가 된다.
| INF | INF | INF | INF | INF |
[Iteration 1]
첫 번째로 노드 1번을 먼저 탐색해보자.
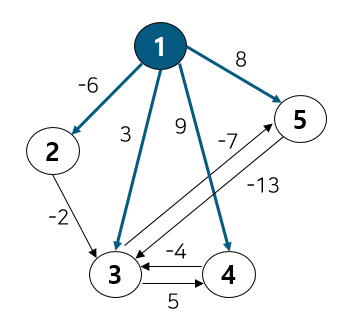
1번 노드에 연결된 인접노드에 해당하는 간선의 가중치를 업데이트 해준다.
| 0 | 3 | 5 | 6 | 9 |
가중치 업데이트에 있어 시작 노드는 사이클이 없으므로 0이 되고, 2~5모두 연결된 간선이 있으므로 해당 가중치 값을 업데이트 해준다.
[Iteration 1]
이제 2번 노드를 보자. 2번 노드는 3번과 연결되어 있다.
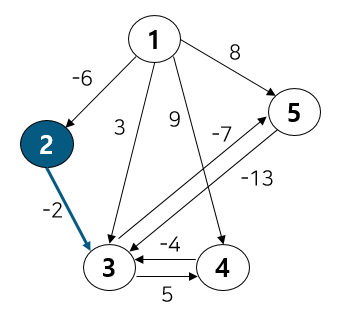
1 → 3 경로 비용인 3보다
1 → 2 → 3 경로 비용인 -8이 더 작으므로 DP 테이블 값을 3에서 -8로 업데이트 해준다.
| 0 | -6 | -8 | 9 | 8 |
[Iteration 1]
이제 3번 노드를 보자. 4번과 5번 노드에 연결되어 있다.

1 → 4 비용인 9보다
1 → 2 → 3 → 4 비용인 -3이 작으므로 9를 -3으로 업데이트 해준다.
| 0 | -6 | -8 | -3 | 8 |
또
1 → 5 비용인 8보다
1 → 2 → 3 → 5 비용인 -15가 작으므로 8을 -15로 업데이트 해준다.
| 0 | -6 | -8 | -3 | -15 |
[Iteration 1]
이제 4번 노드를 보자. 3번 노드와 연결되어 있다.
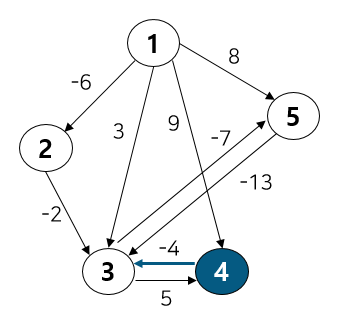
DP 테이블의 3번에 담긴 비용인 -8이
1 → 4 → 3 비용인 5보다 작으므로 업데이트 하지 않는다.
| 0 | -6 | -8 | -3 | -15 |
[Iteration 1]
이제 5번 노드를 보자. 3번 노드와 연결되어 있다.
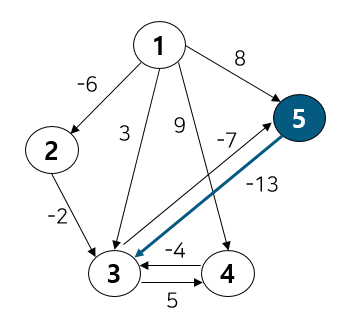
DP 테이블 3번의 -8이
1 → 5 → 3의 비용 -5보다 더 작으므로 업데이트 하지 않는다.
| 0 | -6 | -8 | -3 | -15 |
이를 노드 개수(V) - 1까지 반복 진행한다. 그리고 추가적으로 음의 사이클의 존재 여부를 파악하고 싶다면 마지막으로 1번더 반복하여 총 V번의 반복 했을 때 V-1번 했을 때와 값이 달라진다면 음의 사이클이 있는 것이라 판별할 수 있다. 음의 사이클이 있다면 반복시 무한히 작아지기 때문이다.
Iteration1 종료시 [inf, 0, -6, -8, -3, -15]
Iterataion2 종료시 [inf, 0, -6, -28, -23, -35]
Iteration3 종료시 [inf, 0, -6, -48, -43, -55]
Iteration4 종료시 [inf, 0, -6, -68, -63, -75]
가되며 마지막으로 여기서 한 번더 수행했을 때 값이 바뀐다면 음의 사이클이 존재하는 것이다.
Iteration5 종료시 [inf, 0, -6, -88, -63, -75]
이를 코드로 구현하면 다음과 같다.
"""
5 9
1 2 -6
1 3 3
1 4 9
1 5 8
2 3 -2
3 4 5
3 5 -7
4 3 -4
5 3 -13
"""
import sys
input = sys.stdin.readline
def bellman_ford(start):
weights[start] = 0
for i in range(V):
for src, dst, weight in graph:
W = weights[src] + weight
if weights[src] != INF and weights[dst] > W:
weights[dst] = W
if i == V -1:
return False # negative cycle exists
return True # there is no cycle
V, E = map(int, input().split())
graph = []
for _ in range(E):
src, dst, weight = map(int, input().split())
graph.append([src, dst, weight])
INF = float('inf')
weights = [INF] * (V+1)
if bellman_ford(1): # 출발 노드를 인자 값으로 넣어줄 것
for i in range(2, V+1): # 출발 노드인 1을 제외하고 다른 모든 노드로 가기 위한 최단 거리 출력
print (weights[i], end = ' ')
else:
print ("There is negative cycle.")
위의 알고리즘을 활용하여, 백준 1865-웜홀 문제를 해결할 수 있다.
참고로 시간 복잡도는 $O(VE)$ 이다.
3. 플로이드 워셜 (Floyd Warshall) 알고리즘
플로이드 워셜 알고리즘은 모든 노드 간의 최단거리를 구할 수 있다. 한 노드에서 다른 모든 노드까지의 최단 거리를 구하는 다익스트라와 벨만포드 알고리즘과 대조된다. 플로이드 워셜 알고리즘은 그래프 상에서 음의 가중치가 있더라도 최단 경로를 구할 수 있다. 하지만 음의 가중치와 별개로 음의 사이클이 존재한다면 벨만 포드 알고리즘을 사용해야 한다.
플로이드 워셜 알고리즘은 모든 노드 간의 최단거리를 구하고 이 때, 점화식이 사용되기에 동적 계획법에 해당한다. 동적 계획법에 해당하므로 최단 거리를 업데이트할 테이블이 필요하다. 이 때 모든 노드간의 최단 거리이므로 2차원 배열이 사용된다. 특정 한 노드에서 출발하는 다익스트라가 1차원 배열을 사용하는 것과 차이점이 있다.
플로이드 워셜 알고리즘의 핵심은 각 단계마다 특정한 노드 k를 거쳐 가는 경우를 확인한다. 아래 점화식을 살펴보면 다음과 같다.
$D_{ij} = min(D_{ij}, D_{ik} + D_{kj})$
$i$에서 $j$로 가는 것과 $i$에서 $k$를 거쳐 $j$로 가는 것 중 어느 것이 최소 비용인지를 찾는 것이다.
구현은 매우 간단하여 3중 for문이 사용된다. 아래 코드는 위 점화식을 기반으로 코드화 시킨 것이다.
for k in range(1, V+1): # via
graph[k][k] = 0 # 사이클 없으므로 자기 자신 0
for i in range(1, V+1): # src
for j in range(1, V+1): # dst
graph[i][j] = min(graph[i][j], graph[i][k]+graph[k][j])
코드와 함께 동작 과정을 아래 그래프를 통해 살펴보자.
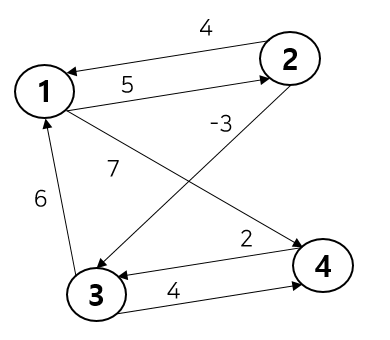
노드 4개와 간선 7개로 구성된 그래프다. 이를 바탕으로 DP 테이블 초기 상태를 만들면 다음과 같다. 하나의 노드에서 다른 노드로 바로 갈 수 있다면 가중치를, 없다면 INF를 저장해준다.
| INF | 5 | INF | 7 |
| 4 | INF | -3 | INF |
| 6 | INF | INF | 4 |
| INF | INF | 2 | INF |
이제 3중 for문을 사용해 거쳐가는 노드를 설정 후 해당 노드를 거쳐갈 때 비용이 줄어드는 경우 값을 업데이트 시켜줄 것이다. 먼저 거쳐가는(k) 노드가 1일 때의 경우를 살펴보자
[Iteration 1] 거쳐가는 노드 K = 1

Iteration 1의 테이블 첫 번째 행을 업데이트 해보자. 노드 1에서 노드 1을 거쳐 노드 1~4까지 탐색하는 경우이다.
graph[1][1] = min(graph[1][1], graph[1][1]+graph[1][1]) : 0과 0+0을 비교하므로 업데이트 X(graph[k][k] = 0)
graph[1][2] = min(graph[1][2], graph[1][1]+graph[1][2]) : 5와 0+5를 비교하는 것이므로 업데이트 X
graph[1][3] = min(graph[1][3], graph[1][1]+graph[1][3]): INF와 0+INF를 비교하는 것이므로 업데이트 X
graph[1][4] = min(graph[1][4], graph[1][1]+graph[1][4]): 7과 0+7을 비교하는 것이므로 업데이트 X
Iteration 1의 테이블 첫 번째 행을 업데이트 한 결과는 다음과 같다. 업데이트는 없었으므로 전과 동일하다. 다만 graph[k][k] = 0에 의해 첫번째 값만 INF에서 0으로 바뀌었다.
| 0 | 5 | INF | 7 |
| 4 | INF | -3 | INF |
| 6 | INF | INF | 4 |
| INF | INF | 2 | INF |
Iteration 1의 테이블 두 번째 행을 업데이트 해보자. 노드 2에서 노드 1을 거쳐 노드 1~4까지 탐색하는 경우이다.
graph[2][1] = min(graph[2][1], graph[2][1]+graph[1][1]): 4와 4+0을 비교하는 것이므로 업데이트 X
graph[2][2] = min(graph[2][2], graph[2][1]+graph[1][2]): INF와 4+9를 비교하는 것이므로 업데이트 O
graph[2][3] = min(graph[2][3], graph[2][1]+graph[1][3]): -3과 4+INF를 비교하는 것이므로 업데이트 X
graph[2][4] = min(graph[2][4], graph[2][1]+graph[1][4]): INF와 4+7을 비교하는 것이므로 업데이트 O
Itertaion 1의 테이블 두 번째 행을 업데이트 한 결과는 다음과 같다. 업데이트는 두 번 이뤄졌다.
| 0 | 5 | INF | 7 |
| 4 | INF → 9 | -3 | INF → 11 |
| 6 | INF | INF | 4 |
| INF | INF | 2 | INF |
Iteration 1의 테이블 세 번째 행을 업데이트 해보자. 노드 3에서 노드 1을 거쳐 노드 1~4까지 탐색하는 경우이다.
graph[3][1] = min(graph[3][1], graph[3][1]+graph[1][1]): 6과 6+0을 비교하는 것이므로 업데이트 X
graph[3][2] = min(graph[3][2], graph[3][1]+graph[1][2]): INF와 11을 비교하는 것이므로 업데이트 O
graph[3][3] = min(graph[3][3], graph[3][1]+graph[1][3]): INF와 6+INF를 비교하는 것이므로 업데이트 X
graph[3][4] = min(graph[3][4], graph[3][1]+graph[1][4]): 4와 13을 비교하고 원래 4였으므로 업데이트 X
Itertaion 1의 테이블 세 번째 행을 업데이트 한 결과는 다음과 같다. 업데이트는 한 번 이뤄졌다.
| 0 | 5 | INF | 7 |
| 4 | 9 | -3 | 11 |
| 6 | INF → 11 | INF | 4 |
| INF | INF | 2 | INF |
Iteration 1의 테이블 네 번째 행을 업데이트 해보자. 노드 4에서 노드 1을 거쳐 노드 1~4까지 탐색하는 경우이다.
graph[4][1] = min(graph[4][1], graph[4][1]+graph[1][1]): INF와 INF+0을 비교하므로 업데이트 X
graph[4][2] = min(graph[4][2], graph[4][1]+graph[1][2]): INF와 INF+5를 를 비교하므로 업데이트 X
graph[4][3] = min(graph[4][3], graph[4][1]+graph[1][3]): 2와 INF+INF를 비교하고 원래 2였으므로 업데이트 X
graph[4][4] = min(graph[4][4], graph[4][1]+graph[1][4]): INF와 INF+7을 비교하므로 업데이트 X
Itertaion 1의 테이블 네 번째 행을 업데이트 한 결과는 다음과 같다. 업데이트는 이뤄지지 않았다.
| 0 | 5 | INF | 7 |
| 4 | 9 | -3 | 11 |
| 6 | 11 | INF | 4 |
| INF | INF | 2 | INF |
이러한 과정을 노드의 수만큼 반복해주면 된다. 이를 요약하면 다음과 같다.
Iteration2는 노드 1~4에서 노드2를 거쳐 노드 1~4를 탐색하는 경우가 될 것이다.
Iteration3은 노드 1~4에서 노드3을 거쳐 노드 1~4를 탐색하는 경우가 될 것이다.
Iteration4는 노드 1~4에서 노드4를 거쳐 노드 1~4를 탐색하는 경우가 될 것이다.
이를 코드로 나타내면 앞서 본 것과 동일하다. 중요한 것은 거쳐서 노드 k를 거쳐갈때 다이렉트로 가는 것보다 비용이 적어지는가를 판단하는 것이다.
for k in range(1, V+1): # via
graph[k][k] = 0 # 사이클 없으므로 자기 자신 0
for i in range(1, V+1): # src
for j in range(1, V+1): # dst
graph[i][j] = min(graph[i][j], graph[i][k]+graph[k][j])
이러한 플로이드 워셜 알고리즘을 구현하는 전체 코드는 다음과 같다.
""" This is input value. you can just copy and paste it.
4 7
1 2 5
1 4 7
2 1 4
2 3 -3
3 1 6
3 4 4
4 3 2
"""
import sys
input = sys.stdin.readline
V, E = map(int, input().split())
INF = float('inf')
graph = [[INF] * (V+1) for _ in range(V+1)]
for _ in range(E):
src, dst, weight = map(int, input().split())
graph[src][dst] = weight
for k in range(1, V+1): # via
graph[k][k] = 0
for i in range(1, V+1): # src
for j in range(1, V+1): # dst
graph[i][j] = min(graph[i][j], graph[i][k]+graph[k][j])
for i in range(1, V+1):
for j in range(1, V+1):
print (graph[i][j], end= ' ')
print()
3중 for문을 사용하므로 시간복잡도는 $O(N^3)$가 된다.
이러한 플로이드 워셜 알고리즘을 이용하여 백준 11404번 플로이드 문제를 해결할 수 있다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 최소 신장 트리와 크루스칼 알고리즘 (0) | 2022.10.06 |
|---|---|
| [자료구조] 링크드 리스트 (Linked List) (1) | 2022.09.05 |
| [자료구조] 이진 탐색 알고리즘 (Binary Search Algorithm) (0) | 2022.08.22 |
| [자료구조] 기본 정렬 알고리즘 총 정리 (4) | 2022.08.13 |