최적화 문제
최적화 문제(Optimization Probelm)란 어떤 목적 함수(Objective Function)의 결과 값을 최적화(최대화 또는 최소화)시키는 파라미터(변수)의 조합을 찾는 문제를 의미한다.
최적화 문제는 보통 영상 처리와 같은 Computer Vision 분야에 있어 마주하는 많은 문제들이 최적화 문제로 귀결되는 경우가 많다.
목적 함수
목적 함수의 최적화 문제는 크게 4가지로 이루어지며 다음과 같다.
일변수 함수의 최적화 문제
- 목적 함수가 $f(x) = 5x + 21$과 같이 하나의 파라미터(변수)로 구성되어 있는 경우.
다변수 함수 최적화 문제
- 목적 함수가 $f(x,y) = 2x - 4xy + 6$과 같이 여러 개의 파라미터(변수)로 구성되어 있는 경우.
선형 최적화 문제
- 목적 함수가 $f(x_1, x_2, ..., x_m) = b + a_1 x_1 + a_2 x_2 + ... + a_m x_m$과 같이 모든 파라미터(변수)에 대해 일차 이하의 다항식으로 구성되어 있는 경우.
비선형 최적화 문제
- 목적 함수가 $f(x,y) = y cosx + x$ 또는 $f(x,y) = x^2 + y$ 등과 같이 구성되어 있는 경우.
그리고 목적 함수 외에 파라미터가 만족해야할 별도의 조건이 있는 경우 Constrained Optimization 문제, 별도의 제약조건이 없는 경우를 Unconstrained Optimization 문제라고 한다.
최적화 원리
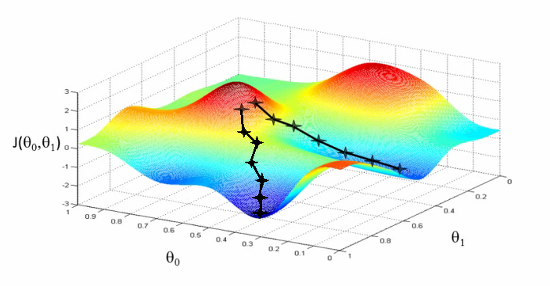
최적화 문제의 본질은 파라미터를 어느 방향으로 얼만큼 움직여서 함수 값을 최적화 시킬 수 있을 것인지에 대한 것이다. 조금씩 조금씩 파라미터의 값과 위치를 변경해가며 더 이상 변경할 수 없는 지점에 도달할 수 있는 파라미터를 찾는 것이며 더 이상 최적화 시킬 수 없는 지점을 Local minima라고 한다.
이러한 최적화를 위해 사용하는 최적화 기법들은 Gradient Decent, Levenberg-Marquardt 방법, 뉴턴 방법 등이 있지만 이러한 기법들의 차이는 결국 이동할 방향과 이동할 크기를 어떤 방식으로 결정하느냐에 대한 차이이다.
이러한 이동할 방향과 크기를 결정하기 위해 기본적으로 사용되는 수학적 원리는 일차미분(기울기)과 이차미분(곡률)의 개념이다.
일차 미분과 이차 미분
- 일차 미분
일차 미분에 사용되는 식은 다음과 같다.
$x_{k+1} = x_k - \lambda f'(x_k)$
$\lambda$의 경우 한번에 얼마나 이동할지 조절하는 step size 파라미터로서 일단은 고정된 상수($\lambda > 0$)로 가정, 아래의 그래프의 함수가 $f(x) = x^4$라 가정, step size 파라미터를 0.01로 설정하면 다음과 같다.
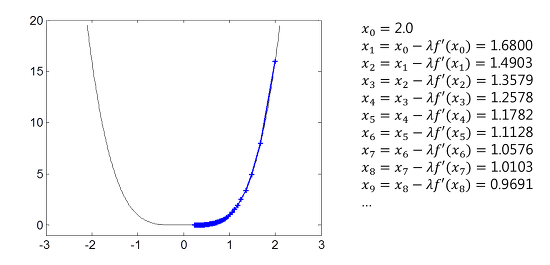
위의 그래프에서 알 수 있는 부분은 일차 미분의 단점으로 극소점 근처에서는 수렴 속도가 현저히 떨어진다는 점이며 그 이유는 극소점에 다가갈수록 $f'(x)$ 값이 0에 가까워져 step size 또한 함께 줄어들기 때문이다.
일차 미분의 이러한 단점을 해결하기 위해서는 step size를 조절하는 것으로 어느 정도 해결할 수 있다.
만약 step size를 0.03(기존의 3배)과 0.13(기존의 13배)와 같이 주게 되면 아래와 같아 진다.

step size를 키우면 위의 왼쪽 그림과 같이 수렴 속도가 증가하긴하나 극소점 근처에서 그 차이가 크지 않다는 점이고, 또한 위의 우측 그림에서 볼 수 있다시피 수렴 속도를 많이 키우게 되면 발산해버리는 문제가 발생하게 된다. 따라서 목적 함수에 마다 값을 최적화 시킬 수 있는 step size 파라미터가 달라질 수 있다.
이러한 일차 미분의 특성을 이용하여 최적화 문제를 해결하는 방법을 Gradient Decent라 한다.
- 이차 미분
위의 일차 미분을 이용한 최적화 기법의 문제를 해결하기 위해서는 일차 미분과 함께 이차 미분을 사용하는 것이다.
$x_{k+1} = {x_k - f'(x_k) \over f''(x_k)}$
앞서 $f(x) = x^4$ 예시에 위의 식을 적용하면, 200번의 반복을 진행한 일차 미분의 결과와 달리, 20번의 반복(iteration)만으로 다음과 같은 수렴 결과를 확인할 수 있다.

일차 미분보다 더 빠른 속도로 0에 수렴할 수 있는 것을 확인할 수 있고, 일차 미분과 달리 $f''(x)$를 이용하여 step size를 조절하기 때문에 일차 미분에서 사용된 $\lambda$ 파라미터 또한 필요로 하지 않는다.
하지만 이러한 이차미분에도 단점이 존재하는데, 이는 변곡점에 있어서 불안정한 형태를 띤다는 것이다. 가령 이차 미분 값이 0이 되면 식이 정의가 되지 않는 문제점이 생길 수 있고, 또한 변곡점 근처에서는 이차 미분 값이 0에 가까운 값을 가지기 때문에 step size가 커져서 엉뚱한 곳으로 발산해버릴 수 있다는 점이다.
더불어 이차미분은 이동할 방향을 정할 때 극대와 극소를 구분하지 않는다는 점도 있다. 예컨데 다음과 같다.
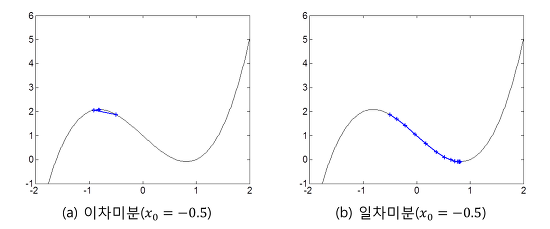
가령 $f(x) = x^3 -2x + 1$에서 $x_0 = 0.5$라 할경우 이차미분에서는 극대점을 향해 수렴하는 반면, 일차미분에서는 극소점을 향해 수렴하게 된다.
이를 정리하자면 결국 일차미분에서는 항상 옳은 방향을 향하지만 step size를 설정하는데 있어 어려움이 있고, 이차미분을 이용한 방법으로는 보다 빠르게 해를 도출할 수 있으나 변곡점(f''=0) 근처에서 문제의 소지가 있으며 극대, 극소를 구분하지 못한다는 단점이 있다.
그동안 연구된 다양한 최적화 기법은 이러한 일차미분, 이차미분의 단점을 극복하기 위한 여러 노력의 결과로 볼수 있다.
일차 미분의 단점을 극복 하기 위해서는 Line Search를 사용하며, 이차미분의 단점을 극복하기 위해서는 Trust Region을 사용한다.
Line Search에도 여러 종류가 있지만 일반적으로 아래와 같은 방법이 있다.
- backtracking line search
- golden section search
Trust Region 방법은 근사 함수에 대한 신뢰 영역을 정의한 후 이동할 목적지에 대한 탐색 범위를 해당 영역 내부로만 제한하는 방법을 의미하며 아래와 같다.

Reference
[1] https://darkpgmr.tistory.com/149
'Artificial Intelligence > 머신러닝-딥러닝' 카테고리의 다른 글
| [Pandas] 데이터 프레임에 컬럼 이름 추가하기 (0) | 2020.05.12 |
|---|---|
| [머신러닝 이론] 서포트 벡터 머신(Support Vector Machine) (0) | 2020.04.12 |
| 머신러닝 파이프라인 (0) | 2020.04.05 |
| 캐글 경진대회 유형 (0) | 2020.04.05 |
| 딥러닝 라이브러리 목록 (0) | 2020.04.05 |