이 포스팅은 『밑바닥부터 시작하는 딥러닝』을 기반으로 작성되었습니다. 간단한 이론이지만 누군가에게 설명할 수 있는가에 대해 생각한 결과, 올바르게 설명하지 못한다고 판단되어 이를 쇄신하고자 하는 마음으로 작성합니다.
1. 신경망의 구조 (Structure of Neural Network)
신경망(neural network)의 구조는 아래와 같이 심플하게 입력 레이어(Input layer), 은닉 레이어(hidden layer), 출력 레이어(output layer)로 총 3개의 레이어(layer)로 구성된다.
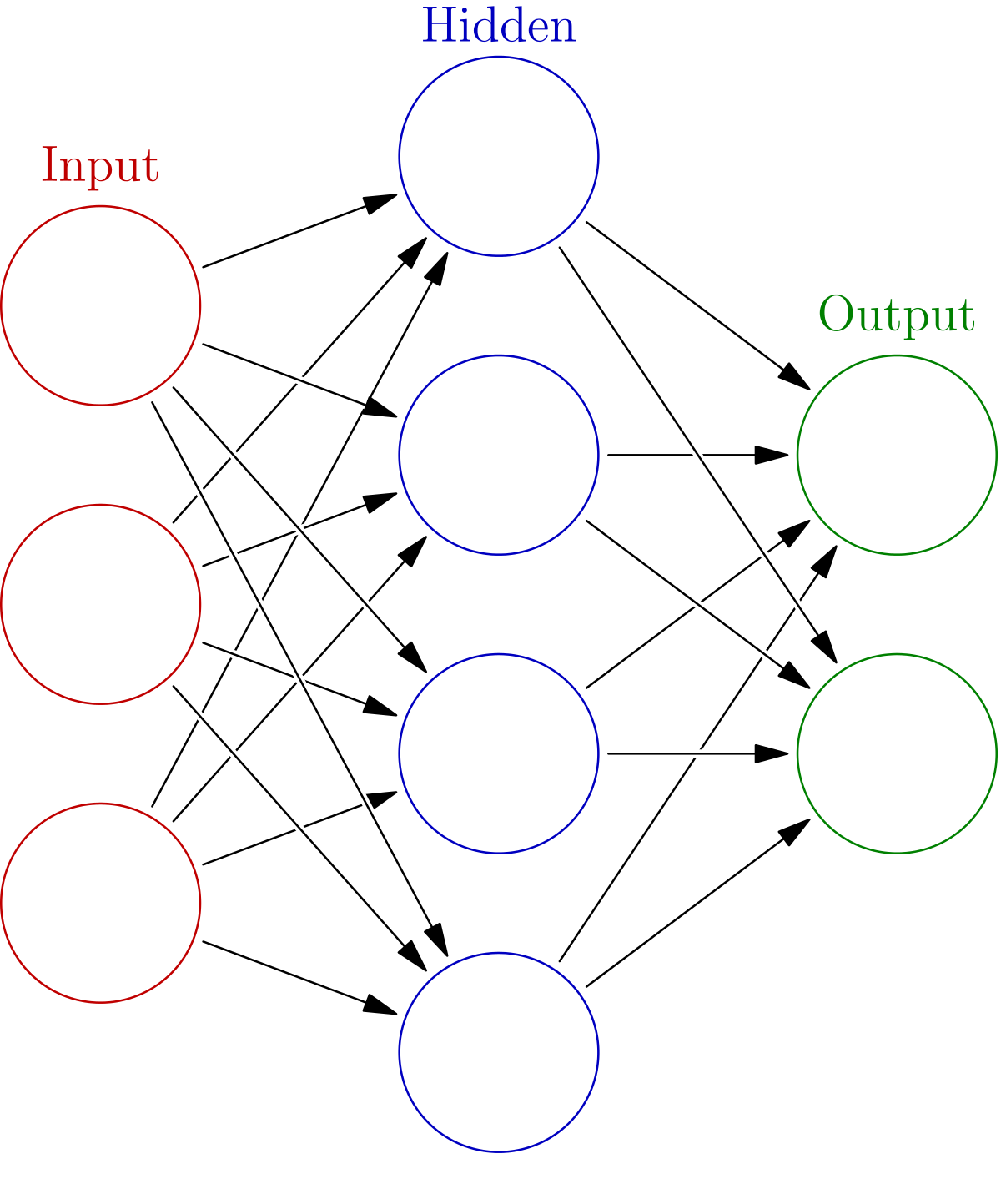
위 신경망의 구조는 레이어가 3개이므로 3층 레이어라고 표현하지만, 정확히는 입력 레이어와 은닉 레이어 사이, 은닉 레이어와 출력 레이어 사이에 있는 가중치를 기준으로 하기 때문에 2층 레이어라 표현하는 것이 일반적이다. 입력 레이어와 출력 레이어는 하나씩 존재한다. 하지만 은닉 레이어를 여러 개 쌓음으로써 신경망의 층을 깊게(크게) 만들 수 있게 된다.
2. 활성화 함수 (Activation Function)
위 그림에서 보는 신경망은 퍼셉트론(Perceptron)과 어떻게 다를까? 본질적으로 신경망과 퍼셉트론은 구조적으로 동일한 형태이다. 하지만 핵심 차이점은 활성화 함수의 차이이다. 그렇다면 활성화 함수란 무엇일까? 아래 그림을 확인해보자.
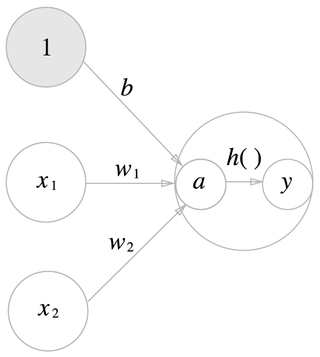
위 그림에서 활성화 함수는 $h()$이다. $h()$의 역할은 입력 신호(x1, x2)와 가중치 (w1, w2)를 곱한 것과 편항(b)의 합인 $a$를 기준으로 활성화 할지(1) 활성화 하지 않을지(0) 여부를 결정하는 함수이다.
다시 말해 간단하게 퍼셉트론을 구성했던 수식은 1)과 같다. 이 때 활성화 함수는 입력 신호와 가중치의 곱 그리고 편향의 합을 입력으로 하는 수식 2)가 된다. 수식 2)의 활성화 함수 $h()$를 통해 신호의 합이 활성화(1) 할지 활성화 하지 않을지(0) 표현하는 함수이다.
$1)\ y = \begin{cases} 0\ (b + x_1w_1 +x_2w_2\leq\theta \\ 1\ (b+x_1w_2+x_2w_2\gt\theta)\end{cases}$
$2)\ y = h(b + w_1x_1+w_2x_2)$
$3)\ h(x) = \begin{cases} 0\ (x\leq0) \\ 1\ (x\gt0)\end{cases}$
퍼셉트론은 위와 같이 활성화 함수로 계단형 함수를 사용했다. 계단형 함수란 값이 연속적(continuous)이지 않고 이산적(discrete)인 특징을 갖는 함수를 말한다. 예컨데 계단 함수를 코드로 구현한 것과 그래프로 나타낸 것은 다음과 같다.
2.1 계단 함수 구현과 그래프 (Step Function & Graph)
import numpy as np
import matplotlib.pyplot as plt
def step_function(x):
return np.array(x > 0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()간단히 다시 말해 계단 함수는 x가 0보다 크면 활성화(1) 작으면 비활성화(0)를 하는 것이다. 계단 함수는 x=0을 기준으로 하여 비활성화(0) 활성화(1)가 뚜렷하게 나뉜다.
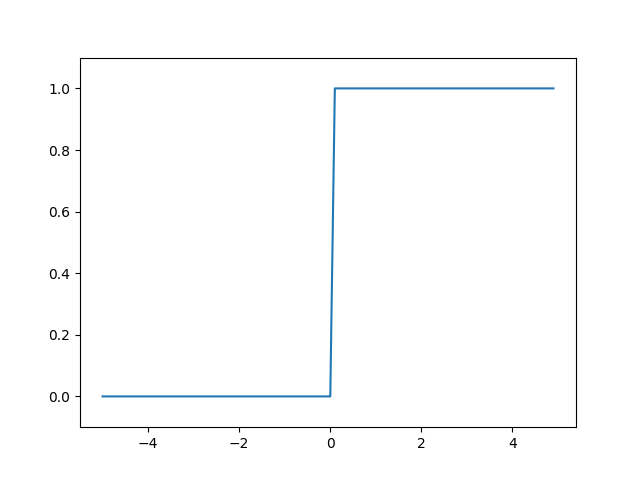
퍼셉트론은 이러한 계단 함수를 사용하는 데, 이러한 계단 함수의 단점은 비연속적/이산적이기 때문에 “매끄러움”을 갖지 못한다는 것에 있다. 따라서 이 퍼셉트론을 신경망으로 동작해줄 수 있게 하기 위해서는 비연속적인 활성화 함수가 아닌 연속적인 활성화 함수를 사용해야 한다. 즉 다른 말로 비선형 활성화 함수를 사용해야 하는 것이다. 대표적인 비선형 활성화 함수에는 시그모이드(Sigmoid) 함수가 있다.
2.2 시그모이드 함수 구현과 그래프 (Sigmoid Function & Graph)
시그모이드(Sigmoid) 함수란 S자 형태의 띠는 함수를 의미한다. 신경망(뉴럴넷)에 사용되는 대표적인 비선형 활성화 함수로 간단하게 코드로 구현한 것과 함수의 그래프는 다음과 같다.
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
간단하게 코드를 설명하면 시그모이드 함수는 내부적으로 자연상수 $e(=2.7182...)$를 사용한다. 자연상수를 기반으로한 시그모이드 함수는 계단 함수와 마찬가지로 동일한 입력 신호 $x$를 입력으로 준 뒤 그래프로 나타내면 아래와 같다.
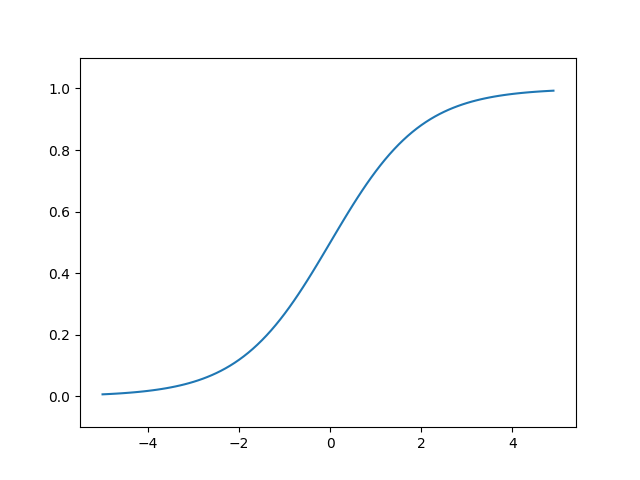
계단 함수와 비교해 연속적이고 매끄러운 형태를 갖는 다는 것을 확인할 수 있다. 앞서 설명했듯 퍼셉트론과 신경망의 핵심 차이는 활성화 함수라고 했다. 퍼셉트론의 경우 이산적인 정수를 출력(0, 1)하는 반면 신경망의 경우 연속적인 실수를 출력(0.1, 0.2, 0.3, ...) 한다. 그렇다면 왜 매끈한 형태를 갖는 비선형 함수가 신경망과 퍼셉트론의 차이를 결정짓는 것일까?
그 이유는 이산적인 특징을 갖는 선형 함수를 사용하게 된다면 층을 깊게 하는 것에 의미가 없기 때문이다. 예를 들면 선형 함수 $h(x) = cx$가 있다고 가정할 경우 3층으로 쌓으면 $y(x) = h(h(h(x)))$가 된다. 하지만 이 계산은 $y(x) = ax$와 동일한 식이다. 단순히 $a=c^3$이라고 치환하면 끝인 것이다. 즉, 은닉층 없는 네트워크로 표현이 가능하게 된다. 이와 같은 예시처럼 선형 함수를 이용하면 여러 층으로 구성하는 신경망의 이점을 살릴 수 없다. 따라서 층을 쌓는 이점을 얻기 위해서는 활성화 함수를 반드시 비선형 함수를 사용해야 한다.
그렇다면 또 다른 비선형 함수들의 종류와 특징들은 어떤 것들이 있을까? 추가적으로 더 알아보자.
2.3 ReLU 함수 구현과 그래프 (ReLU Function & Graph)
시그모이드 함수는 신경망에서 자주 사용되었으나 최근에는 시그모이드 대신 ReLU를 주로 사용한다. ReLU란 입력 값이 0보다 작으면 0을 출력하고 0보다 크면 입력 값을 그대로 출력하는 함수이다. 코드로 구현한 것과 ReLU 함수를 그래프로 나타낸 것은 아래와 같다.
import numpy as np
import matplotlib.pyplot as plt
def ReLU(x):
return np.maximum(0, x)
x = np.arange(-6, 6, 1)
y = ReLU(x)
plt.plot(x, y)
plt.ylim(-1, 6)
plt.show()
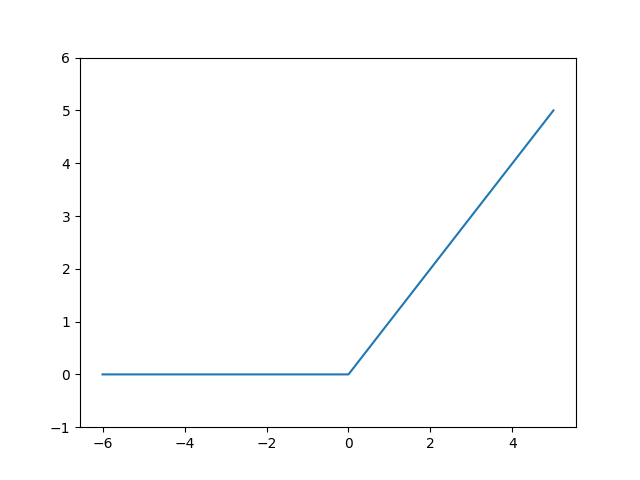
다시 말해 입력 값이 0보다 작으면 0으로 출력하고 입력 값이 0보다 크다면 입력 값을 그대로 출력한다. 하지만 이런 ReLU 함수의 한계점은 한 번 활성화 값이 0인 출력값을 다음 레이어의 입력으로 전달하게 되면 이후 뉴런들의 출력 값이 모두 0이 되는 현상이 발생하는 것이다. 이를 dying ReLU라 하며 이러한 한계점을 개선하기 위해 음수 값을 일부 표현할 수 있도록 개선한 활성화 함수들이 사용된다. 그 종류로는 LeakyReLU, ELU, PReLU, ThresholdReLU, Softplus, Swish 등이 있다.
2.4 항등 함수 및 소프트맥스 함수의 구현과 그래프
출력층의 활성화 함수는 풀고자 하는 문제에 적합한 활성화 함수를 사용해야 한다. 예를 들면 분류 문제와 회귀 문제가 있다. 분류 문제는 크게 이중 분류와 다중 분류로 나뉜다. 이중 분류를 한다면 시그모이드 함수를 사용하는 것이 적합하고, 다중 분류를 사용한다면 소프트맥스 함수를 사용하는 것이 적합하다. 그리고 회귀 문제의 경우는 항등 함수를 사용하는 것이 적합하다. 그렇다면 소프트맥스 함수와 항등 함수는 무엇일까?
먼저 항등 함수의 경우 ReLU와 비슷한 맥락으로 입력 값 자기 자신을 출력하는 함수를 의미한다. ReLU와 다른점이 있다면 음수 입력도 그대로 출력하는 것이다. 코드로 표현하면 아래와 같다.
def identity_function(x)
return x소프트맥스 함수는 다중 분류에 사용된다 했다. 소프트맥스 함수를 한 마디로 표현하면 분류해야 할 출력 개수에 대해 각각의 확률을 출력하는 함수이다. 예를 들어 이 사진이 강아지, 고양이, 원숭이인지 분류해야할 다중 분류에는 어떤 한 사진이 입력 신호로 들어왔을 때 최종 출력으로 강아지일 확률 0.A%, 고양이일 확률 0.B%, 원숭이일 확률 0.C%로 표현하는 것이다. 이 때 소프트맥스 함수의 특징은 A+B+C = 1이 되는 것이다. 즉, 모든 출력 확률의 합은 1이 된다. 그렇다면 이런 소프트맥스 함수는 어떤 형태를 갖고 있을까? 그 형태는 다음과 같다.
$y_k = {exp(a_k)\over \sum_{i=1}^nexp(a_i)}$
여기서 $n$은 출력층의 뉴런 수(=분류해야할 크기), $exp$는 지수함수 $e^x$, $y_k$는 $k$번째 출력을 의미한다. 분모는 모든 입력 신호의 지수 함수 값의 합을 의미하고, 분자는 입력 신호의 지수 함수 값을 의미한다. 이를 코드로 구현하면 다음과 같다.
import numpy as np
a = np.array([0.3, 2.9, 4.0])
def softmax(x):
exp_a = np.sum(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
2.4.1 소프트맥스 함수 한계점과 개선
하지만 위와 같은 소프트맥스 함수에는 한가지 큰 단점이 있다. 바로 오버플로우 문제이다. 지수 함수의 특성상 과도하게 큰 수치의 값을 출력할 수 있게 되어 컴퓨터가 이를 올바르게 표현하지 못할 수 있다. 따라서 컴퓨터로 하여금 이러한 오버플로우 문제를 해결하기 위해서 소프트맥스 함수를 개선하여 구현하는 것이 일반적이다. 핵심 방법은 입력 신호 중 최대값을 빼는 것이다. 코드로 구현하면 다음과 같다.
import numpy as np
a = np.array([0.3, 2.0, 4.0])
def sofmtax(x):
maximum = np.max(a)
exp_a = np.exp(a-c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y이를 수식적으로 설명하면 다음과 같다.
$y_k = {exp(a_k)\over \sum_{i=1}^nexp(a_i)}$
$= {Cexp(a_k) \over C\sum_{i=1}^nexp(a_i)}$
$= {exp(a_k + logC) \over \sum_{i=1}^nexp(a_i+logC)}$
$= {exp(a_k+C')\over \sum_{i=1}^nexp(a_i+C')}$
즉 C라고 하는 임의의 정수를 곱해준 다음, $log$ 함수로 표현하여 지수 함수 내부로 옮겨준 뒤 마지막으로 $logC$를 $C'$로 치환해주는 식이다. 이러한 방식을 통해 오버플로우 문제를 개선한다. 이렇게 임의의 정수를 초기에 곱해주고 마지막으로 $C'$로 치환해도 함수 상 문제가 없는 것은 분모 분자 모두 동일한 임의의 정수 $C$를 곱해준 것이기 때문에 결론적으로 동일한 계산이 된다. 다른 말로 표현하면 소프트맥스 함수에서 내부적으로 사용되는 지수 함수인 $exp(x)$는 단조증가함수이기 때문에 가능한 것이다. 여기서 단조증가 함수란 $a\leq b$일 때 항상 $f(a)\leq g(b)$가 되는 함수를 의미한다.
Reference
[1] https://phobyjun.github.io/2019/09/12/밑바닥부터-시작하는-딥러닝-신경망.html
[2] https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=cjswo9207&logNo=221059314707
'Artificial Intelligence > 머신러닝-딥러닝' 카테고리의 다른 글
| [자연어처리] 챗봇 시스템 구축 (Rasa 활용) (0) | 2022.11.08 |
|---|---|
| [신경망 이론] 신경망 학습과 손실함수 (Neural Network Training And Loss Function) (0) | 2022.03.17 |
| [신경망 이론] 퍼셉트론 (Perceptron) (0) | 2022.03.15 |
| [자연어 처리] BERT와 GPT로 배우는 자연어 처리 (0) | 2022.02.23 |
| [자연어처리] Word2Vec: Efficient Estimation of Word Representations in Vector Space (0) | 2022.02.10 |