이 포스팅은 『밑바닥부터 시작하는 딥러닝』을 기반으로 작성되었습니다. 간단한 이론이지만 누군가에게 설명할 수 있는가에 대해 생각한 결과, 올바르게 설명하지 못한다고 판단되어 이를 쇄신하고자 하는 마음으로 작성합니다. 

신경망 학습과 손실함수

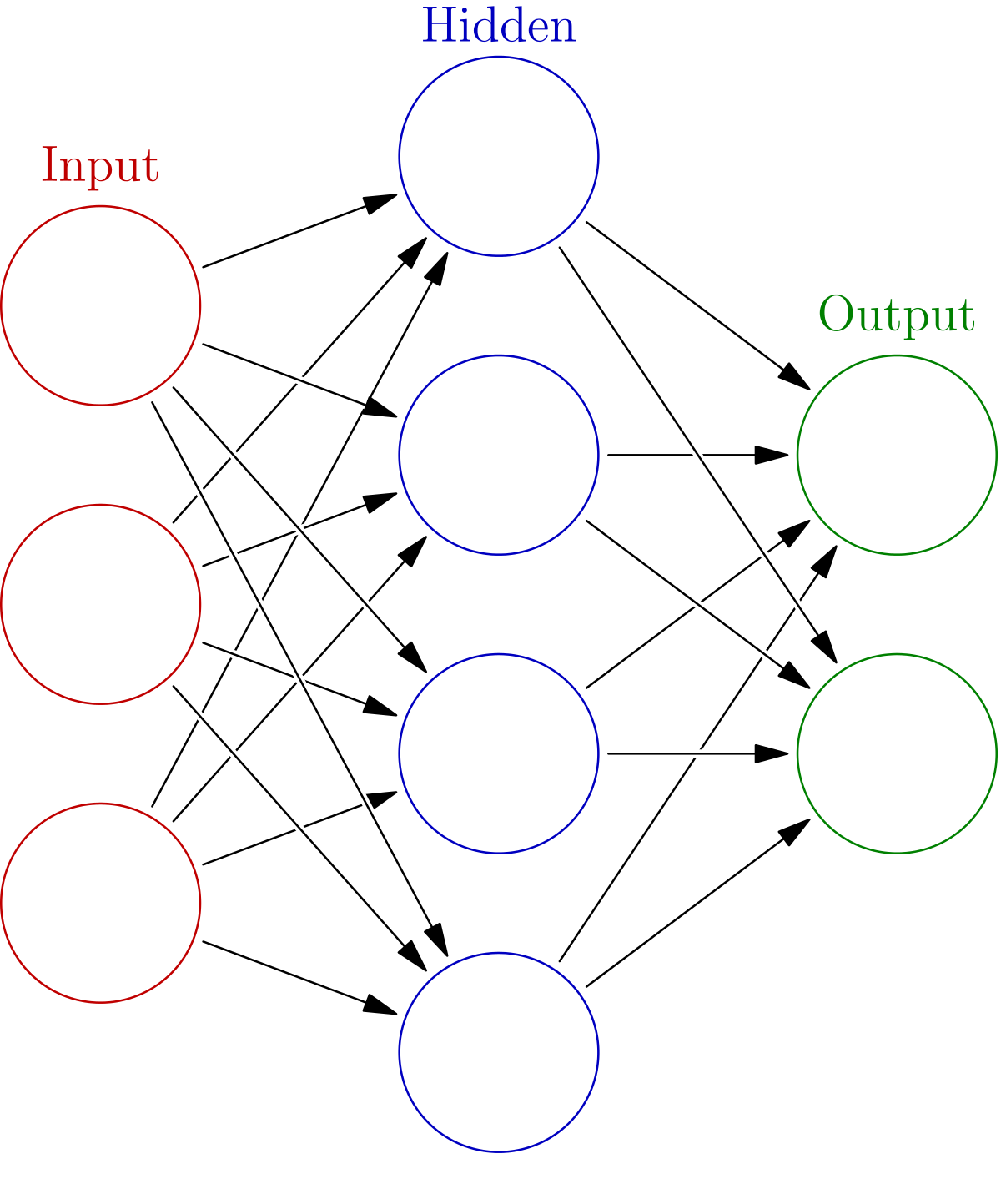
신경망을 학습한다는 것은 훈련 데이터로부터 매개변수(가중치, 편향)의 최적값을 찾아가는 것을 의미한다. 이 때 매개변수가 얼마나 잘 학습되었는지를 어떻게 판단할 수 있을까? 방법은 손실함수(loss function)을 사용하는 것이다. 손실함수란 훈련 데이터로부터 학습된 매개변수를 사용하여 도출된 출력 신호와 실제 정답이 얼마나 오차가 있는지를 판단하는 함수이다. 다시 말해 학습된 신경망으로부터 도출된 결과 값과 실제 정답이 얼마나 차이가 나는지를 계산하는 함수이다. 값의 차이를 손실이라고 말하며 신경망은 이 손실함수의 값이 작아지는 방향으로 매개변수를 업데이트 하게 된다.

그렇다면 신경망의 학습을 위해 사용하는 손실함수의 종류들은 무엇이 있을까? 종류를 논하기에 앞서 손실함수는 풀고자하는 태스크에 따라 달라질 수 있다. 예를 들어 머신러닝 태스크는 크게 분류 태스크와 회귀 태스크가 있을 것이다. 분류 태스크라고 한다면 이 사진이 강아지, 고양이, 원숭이 중 어디에 해당할지 분류 하는 것이다. 분류 태스크의 특징은 실수와 같이 연속적인 것이 아니라 정수와 같이 불연속적으로 정확하게 강아지, 고양이, 원숭이 중 하나로 나눌 수 있다. 반면 회귀 태스크는 연속이 아닌 불연속적(이산적)인 값을 가지는 태스크를 수행하는 것을 의미한다. 예를 들어 사람의 키에 따르는 몸무게 분포를 구하는 태스크일 경우 몸무게와 같은 데이터는 실수로 표현할 수 있기 때문에 출력 값이 연속적인 특징을 가지는 회귀 태스크라 할 수 있다.

그렇다면 손실함수의 종류와 특징들에 대해서 알아보도록 하자.

손실함수 (Loss Function)

평균제곱오차 (Mean Squared Error, MSE)

여러 종류의 손실함수 중 평균제곱오차라는 손실함수가 있다. 이 손실함수를 수식으로 나타내면 다음과 같다.

$$ MSE = {1\over n}\sum_i^n(\hat{y}_i - y_i)^2 $$

간단한 수식이다. 천천히 살펴보자면, $\hat{y}_i$는 신경망의 출력 신호이며 $y_i$는 실제 정답이다. $n$은 학습 데이터 수를 의미한다. 이를 해석하자면 출력(예측) 신호와 실제 정답 간의 차이를 구한다음 제곱을 해준 값을 데이터셋 수 만큼 반복하며 더해주는 것이다. 제곱을 해주는 이유는 음수가 나오는 경우를 대비하여 마이너스 부호를 없애기 위함이다. $1\over n$를 곱해주는 이유는 평균 값을 구해주기 위함이다. 즉 MSE를 한마디로 이야기하면 오차의 제곱을 평균으로 나눈다고 할 수 있다. 따라서 MSE는 값이 작으면 작을 수록 예측과 정답 사이의 손실이 적다는 것이므로 좋다.

import numpy as np

def mean_squared_error(output, real):
    mse_loss = 1 / len(output) * np.sum((output - real) ** 2)
    return mse_loss

output = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0] # 후보별 정답일 확률
real = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] # 정답 = 2

mse_loss = mean_squared_error(np.array(output), np.array(real)) # input type = numpy array
print (mse_loss) # 0.0195
--------------------
output = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] # 후보별 정답일 확률
mse_loss = mean_squared_error(np.array(output), np.array(real))
print (mse_loss) # 0.1195

출력 신호인, 예측 확률 output이 가지고 있는 가장 높은 확률 값과 정답이 차이가 적을수록 손실 함수의 출력 값도 적은 것을 확인할 수 있다. 반면 가장 높은 확률이 정답이 아닌 다른 곳을 가리킬 때 손실함수의 출력 값이 커지는 것을 확인할 수 있다. 위에서 볼 수 있듯 평균제곱오차(MSE)는 분류 태스크에 사용 된다.

교차 엔트로피 오차 (Cross-Entropy Error, CEE)

위와 달리 회귀 태스크에 사용하는 손실함수로 교차 엔트로피 오차가 있다. 수식으로 나타내면 다음과 같다.

$$ CEE = -\sum_i\hat{y_i}\ log_e^{y_i} $$

$\hat{y_i}$는 신경망의 출력이며 $y_i$는 실제 정답이다. 특히 $\hat{y_i}$는 one-hot encoding으로 정답에 해당하는 인덱스 원소만 1이며 이외에는 0이다. 따라서 실질적으로는 정답이라 추정될 때($\hat{y_i}=1$)의 자연로그를 계산하는 식이 된다. 즉 다시 말해 교차 엔트로피 오차는 정답일 때의 출력이 전체 값을 정하게 된다.

import numpy as np

def cross_entropy_error(output, real):
	delta = 1e-7
	cee_loss = -np.sum(output * np.log(real + delta))
	return cee_loss

output = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] # 예측 정답 = 2번째
real = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.10] # 2번째가 정답일 확률 = 0.6
print (cross_entropy_error(np.array(output), np.array(real))) # 0.510825457099338

real = [0.1 , 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0] # 7번째가 정답일 확률 = 0.6
print (cross_entropy_error(np.array(output), np.array(real))) # 2.302584092994546

실제로 구현할 때는 log가 무한대가 되어 계산 불능이 되지 않도록 하기 위해 delta 값을 더해주는 방식으로 구현한다. 예측 정답이 2번이고 실제 정답이 2번일 경우의 손실함수 값은 0.051이고 이와 달리 예측 정답이 2번이고 실제 정답이 7번일 경우 손실함수 값은 2.302가 된다. 즉, 정답에 가까울수록 손실함수는 줄어들고 오답에 가까울수록 손실함수는 커진다고 볼 수 있다. 신경망의 목표는 이러한 손실함수의 값을 줄이는 방향으로 학습하는 것이다.

이 포스팅은 『밑바닥부터 시작하는 딥러닝』을 기반으로 작성되었습니다. 간단한 이론이지만 누군가에게 설명할 수 있는가에 대해 생각한 결과, 올바르게 설명하지 못한다고 판단되어 이를 쇄신하고자 하는 마음으로 작성합니다. 

1. 신경망의 구조 (Structure of Neural Network)

신경망(neural network)의 구조는 아래와 같이 심플하게 입력 레이어(Input layer), 은닉 레이어(hidden layer), 출력 레이어(output layer)로 총 3개의 레이어(layer)로 구성된다. 

위 신경망의 구조는 레이어가 3개이므로 3층 레이어라고 표현하지만, 정확히는 입력 레이어와 은닉 레이어 사이, 은닉 레이어와 출력 레이어 사이에 있는 가중치를 기준으로 하기 때문에 2층 레이어라 표현하는 것이 일반적이다. 입력 레이어와 출력 레이어는 하나씩 존재한다. 하지만 은닉 레이어를 여러 개 쌓음으로써 신경망의 층을 깊게(크게) 만들 수 있게 된다.

2. 활성화 함수 (Activation Function)

위 그림에서 보는 신경망은 퍼셉트론(Perceptron)과 어떻게 다를까? 본질적으로 신경망과 퍼셉트론은 구조적으로 동일한 형태이다. 하지만 핵심 차이점은 활성화 함수의 차이이다. 그렇다면 활성화 함수란 무엇일까? 아래 그림을 확인해보자.

위 그림에서 활성화 함수는 $h()$이다. $h()$의 역할은 입력 신호(x1, x2)와 가중치 (w1, w2)를 곱한 것과 편항(b)의 합인 $a$를 기준으로 활성화 할지(1) 활성화 하지 않을지(0) 여부를 결정하는 함수이다.

다시 말해 간단하게 퍼셉트론을 구성했던 수식은 1)과 같다. 이 때 활성화 함수는 입력 신호와 가중치의 곱 그리고 편향의 합을 입력으로 하는 수식 2)가 된다. 수식 2)의 활성화 함수 $h()$를 통해 신호의 합이 활성화(1) 할지 활성화 하지 않을지(0) 표현하는 함수이다.

$1)\ y = \begin{cases} 0\ (b + x_1w_1 +x_2w_2\leq\theta \\ 1\ (b+x_1w_2+x_2w_2\gt\theta)\end{cases}$

$2)\ y = h(b + w_1x_1+w_2x_2)$

$3)\ h(x) = \begin{cases} 0\ (x\leq0) \\ 1\ (x\gt0)\end{cases}$

퍼셉트론은 위와 같이 활성화 함수로 계단형 함수를 사용했다. 계단형 함수란 값이 연속적(continuous)이지 않고 이산적(discrete)인 특징을 갖는 함수를 말한다. 예컨데 계단 함수를 코드로 구현한 것과 그래프로 나타낸 것은 다음과 같다.

2.1 계단 함수 구현과 그래프 (Step Function & Graph)

import numpy as np
import matplotlib.pyplot as plt

def step_function(x):
	return np.array(x > 0, dtype=np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

간단히 다시 말해 계단 함수는 x가 0보다 크면 활성화(1) 작으면 비활성화(0)를 하는 것이다. 계단 함수는 x=0을 기준으로 하여 비활성화(0) 활성화(1)가 뚜렷하게 나뉜다.

퍼셉트론은 이러한 계단 함수를 사용하는 데, 이러한 계단 함수의 단점은 비연속적/이산적이기 때문에 “매끄러움”을 갖지 못한다는 것에 있다. 따라서 이 퍼셉트론을 신경망으로 동작해줄 수 있게 하기 위해서는 비연속적인 활성화 함수가 아닌 연속적인 활성화 함수를 사용해야 한다. 즉 다른 말로 비선형 활성화 함수를 사용해야 하는 것이다. 대표적인 비선형 활성화 함수에는 시그모이드(Sigmoid) 함수가 있다.

2.2 시그모이드 함수 구현과 그래프 (Sigmoid Function & Graph)

시그모이드(Sigmoid) 함수란 S자 형태의 띠는 함수를 의미한다. 신경망(뉴럴넷)에 사용되는 대표적인 비선형 활성화 함수로 간단하게 코드로 구현한 것과 함수의 그래프는 다음과 같다.

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

간단하게 코드를 설명하면 시그모이드 함수는 내부적으로 자연상수 $e(=2.7182...)$를 사용한다. 자연상수를 기반으로한 시그모이드 함수는 계단 함수와 마찬가지로 동일한 입력 신호 $x$를 입력으로 준 뒤 그래프로 나타내면 아래와 같다.

계단 함수와 비교해 연속적이고 매끄러운 형태를 갖는 다는 것을 확인할 수 있다. 앞서 설명했듯 퍼셉트론과 신경망의 핵심 차이는 활성화 함수라고 했다. 퍼셉트론의 경우 이산적인 정수를 출력(0, 1)하는 반면 신경망의 경우 연속적인 실수를 출력(0.1, 0.2, 0.3, ...) 한다. 그렇다면 왜 매끈한 형태를 갖는 비선형 함수가 신경망과 퍼셉트론의 차이를 결정짓는 것일까?

그 이유는 이산적인 특징을 갖는 선형 함수를 사용하게 된다면 층을 깊게 하는 것에 의미가 없기 때문이다. 예를 들면 선형 함수 $h(x) = cx$가 있다고 가정할 경우 3층으로 쌓으면 $y(x) = h(h(h(x)))$가 된다. 하지만 이 계산은 $y(x) = ax$와 동일한 식이다. 단순히 $a=c^3$이라고 치환하면 끝인 것이다. 즉, 은닉층 없는 네트워크로 표현이 가능하게 된다. 이와 같은 예시처럼 선형 함수를 이용하면 여러 층으로 구성하는 신경망의 이점을 살릴 수 없다. 따라서 층을 쌓는 이점을 얻기 위해서는 활성화 함수를 반드시 비선형 함수를 사용해야 한다.

그렇다면 또 다른 비선형 함수들의 종류와 특징들은 어떤 것들이 있을까? 추가적으로 더 알아보자.

2.3 ReLU 함수 구현과 그래프 (ReLU Function & Graph)

시그모이드 함수는 신경망에서 자주 사용되었으나 최근에는 시그모이드 대신 ReLU를 주로 사용한다. ReLU란 입력 값이 0보다 작으면 0을 출력하고 0보다 크면 입력 값을 그대로 출력하는 함수이다. 코드로 구현한 것과 ReLU 함수를 그래프로 나타낸 것은 아래와 같다.

import numpy as np
import matplotlib.pyplot as plt

def ReLU(x):
    return np.maximum(0, x)

x = np.arange(-6, 6, 1)
y = ReLU(x)
plt.plot(x, y)
plt.ylim(-1, 6)
plt.show()

다시 말해 입력 값이 0보다 작으면 0으로 출력하고 입력 값이 0보다 크다면 입력 값을 그대로 출력한다. 하지만 이런 ReLU 함수의 한계점은 한 번 활성화 값이 0인 출력값을 다음 레이어의 입력으로 전달하게 되면 이후 뉴런들의 출력 값이 모두 0이 되는 현상이 발생하는 것이다. 이를 dying ReLU라 하며 이러한 한계점을 개선하기 위해 음수 값을 일부 표현할 수 있도록 개선한 활성화 함수들이 사용된다. 그 종류로는 LeakyReLU, ELU, PReLU, ThresholdReLU, Softplus, Swish 등이 있다.

2.4 항등 함수 및 소프트맥스 함수의 구현과 그래프

출력층의 활성화 함수는 풀고자 하는 문제에 적합한 활성화 함수를 사용해야 한다. 예를 들면 분류 문제와 회귀 문제가 있다. 분류 문제는 크게 이중 분류와 다중 분류로 나뉜다. 이중 분류를 한다면 시그모이드 함수를 사용하는 것이 적합하고, 다중 분류를 사용한다면 소프트맥스 함수를 사용하는 것이 적합하다. 그리고 회귀 문제의 경우는 항등 함수를 사용하는 것이 적합하다. 그렇다면 소프트맥스 함수와 항등 함수는 무엇일까?

먼저 항등 함수의 경우 ReLU와 비슷한 맥락으로 입력 값 자기 자신을 출력하는 함수를 의미한다. ReLU와 다른점이 있다면 음수 입력도 그대로 출력하는 것이다. 코드로 표현하면 아래와 같다.

def identity_function(x)
	return x

소프트맥스 함수는 다중 분류에 사용된다 했다. 소프트맥스 함수를 한 마디로 표현하면 분류해야 할 출력 개수에 대해 각각의 확률을 출력하는 함수이다. 예를 들어 이 사진이 강아지, 고양이, 원숭이인지 분류해야할 다중 분류에는 어떤 한 사진이 입력 신호로 들어왔을 때 최종 출력으로 강아지일 확률 0.A%, 고양이일 확률 0.B%, 원숭이일 확률 0.C%로 표현하는 것이다. 이 때 소프트맥스 함수의 특징은 A+B+C = 1이 되는 것이다. 즉, 모든 출력 확률의 합은 1이 된다. 그렇다면 이런 소프트맥스 함수는 어떤 형태를 갖고 있을까? 그 형태는 다음과 같다.

$y_k = {exp(a_k)\over \sum_{i=1}^nexp(a_i)}$

여기서 $n$은 출력층의 뉴런 수(=분류해야할 크기), $exp$는 지수함수 $e^x$, $y_k$는 $k$번째 출력을 의미한다. 분모는 모든 입력 신호의 지수 함수 값의 합을 의미하고, 분자는 입력 신호의 지수 함수 값을 의미한다. 이를 코드로 구현하면 다음과 같다.

import numpy as np

a = np.array([0.3, 2.9, 4.0])

def softmax(x):
    exp_a = np.sum(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

2.4.1 소프트맥스 함수 한계점과 개선

하지만 위와 같은 소프트맥스 함수에는 한가지 큰 단점이 있다. 바로 오버플로우 문제이다. 지수 함수의 특성상 과도하게 큰 수치의 값을 출력할 수 있게 되어 컴퓨터가 이를 올바르게 표현하지 못할 수 있다. 따라서 컴퓨터로 하여금 이러한 오버플로우 문제를 해결하기 위해서 소프트맥스 함수를 개선하여 구현하는 것이 일반적이다. 핵심 방법은 입력 신호 중 최대값을 빼는 것이다. 코드로 구현하면 다음과 같다.

import numpy as np

a = np.array([0.3, 2.0, 4.0])

def sofmtax(x):
    maximum = np.max(a)
    exp_a = np.exp(a-c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

이를 수식적으로 설명하면 다음과 같다.

$y_k = {exp(a_k)\over \sum_{i=1}^nexp(a_i)}$

$= {Cexp(a_k) \over C\sum_{i=1}^nexp(a_i)}$

$= {exp(a_k + logC) \over \sum_{i=1}^nexp(a_i+logC)}$

$= {exp(a_k+C')\over \sum_{i=1}^nexp(a_i+C')}$

즉 C라고 하는 임의의 정수를 곱해준 다음, $log$ 함수로 표현하여 지수 함수 내부로 옮겨준 뒤 마지막으로 $logC$를  $C'$로 치환해주는 식이다. 이러한 방식을 통해 오버플로우 문제를 개선한다. 이렇게 임의의 정수를 초기에 곱해주고 마지막으로 $C'$로 치환해도 함수 상 문제가 없는 것은 분모 분자 모두 동일한 임의의 정수 $C$를 곱해준 것이기 때문에 결론적으로 동일한 계산이 된다. 다른 말로 표현하면 소프트맥스 함수에서 내부적으로 사용되는 지수 함수인 $exp(x)$는 단조증가함수이기 때문에 가능한 것이다. 여기서 단조증가 함수란 $a\leq b$일 때 항상 $f(a)\leq g(b)$가 되는 함수를 의미한다.

Reference

[1] https://phobyjun.github.io/2019/09/12/밑바닥부터-시작하는-딥러닝-신경망.html

[2] https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=cjswo9207&logNo=221059314707 

[3] https://yeomko.tistory.com/39

이 포스팅은 『밑바닥부터 시작하는 딥러닝』을 기반으로 작성되었습니다. 간단한 이론이지만 누군가에게 설명할 수 있는가에 대해 생각한 결과, 올바르게 설명하지 못한다고 판단되어 이를 쇄신하고자 하는 마음으로 작성합니다.

1. 퍼셉트론(Perceptron)

퍼셉트론이란 여러 개의 입력 신호를 받아 하나의 출력 신호를 만들어내는 알고리즘이다. 1957년에 고안된 것으로 딥러닝의 기원이된 개념이다. 딥러닝을 이해하기 위한 가장 기초가 되는 개념이다. 그림으로 표현하면 아래와 같다.

$x_1, x_2$는 퍼셉트론이라는 신경망 알고리즘의 입력 신호에 해당한다. $w_1, w_2$는 가중치(weight)로, 입력된 신호가 얼마나 중요한지를 표현하기 위한 매개변수이다. 가중치가 클수록 해당 신호가 그만큼 중요한 것이다. 가중치 $w$는 일종의 전류의 저항과 같이 흐름을 제어하는 요소로써 중요한 입력 신호는 더 큰 신호로 만들어주고 덜 중요한 신호는 비교적 작은 신호로 만들어 주는 역할을 한다. 딥러닝에서 학습을 한다는 것은 입력된 신호를 잘 나타내기 위해 $w_1, w_2$와 같은 가중치를 업데이트 하는 과정이라 할 수 있다. 입력 신호와 출력 신호에 해당하는 둥그런 원들을 뉴런 또는 노드라고 부른다. 입력 신호와 가중치의 곱셈합이 $y$가 되는데 수식으로 나타내면 아래와 같다.

$y = \begin{cases}0\ (x_1w_1+x_2w_2\leq \theta) \\ 1\ (x_1w_1+x_2w_2\gt \theta) \end{cases}$

여기서 $\theta$는 threshold를 의미하는 것으로 사용자가 설정한 임계값을 뜻한다. 입력신호와 가중치의 합이 $\theta$를 넘지 못하면 0을, 넘는다면 1을 출력하는 방식으로 퍼셉트론은 동작한다.

2. 편향

사실 위의 퍼셉트론 개념에는 편향이라는 개념이 포함되는데, 다시 수식으로 나타내면 다음과 같다.

$y = \begin{cases}0\ (b+ x_1w_1+x_2w_2\leq 0) \\ 1\ (b+ x_1w_1+x_2w_2\gt 0) \end{cases}$

$\theta \rightarrow -b$로 치환된 것에 불과하다. 여기서 $b$는 bias를 의미하는 것으로 입력 신호가 얼마나 쉽게 활성화(결과를 1로 출력)하는지를 조정하는 매개변수이다.

예를 들어 $b=-0.5$라면 입력신호와 매개변수의 합 $(x_1w_1+x_2w_2)$의 값이 0.5가 넘어야만 활성화 할 수 있는 것이다.

3. 논리게이트와 퍼셉트론의 한계

퍼셉트론을 통해 컴퓨터의 가장 기본이 되는 논리 게이트를 구현할 수 있다. 논리 게이트 종류는 AND, OR, XOR, NOR, NAND, NOT이 있지만 퍼셉트론을 통해서는 XOR을 구현할 수 없다. XOR이라는 논리게이트를 구현하지 못하는 것은 큰 의미를 갖는다. 논리 게이트는 컴퓨터에 있어 가장 근간이 되는 것이다. 컴퓨터에서 일어나는 연산은 모든 논리 게이트의 합이라 할 수 있다. XOR을 구현할 수 없다는 것은 기본이 되는 연산 중 하나를 못하게 되는 것으로, 복합 논리 연산을 하지 못한다는 것이다. 이 XOR 연산을 하지 못한다는 것이 퍼셉트론의 한계이다.

하지만 정확히는 하나의 층으로 이루어진 싱글레이어 퍼셉트론(single-layer perceptron)으로는 구현할 수 없다는 것이 한계이다. 이를 해결하는 방법이 퍼셉트론을 중첩해서 쌓는 멀티레이어 퍼셉트론(multi-layer perceptron)이다. 퍼셉트론의 아름다움은 여러 개의 층을 쌓는 멀티레이어 퍼셉트론에 있는 것이다.

예를 들면 위 퍼셉트론 기본 구조 그림에서 $x_1, x_2$은 0층이고 $y$는 1층으로 이루어진 싱글레이어 퍼셉트론이라 할 수 있다. 여기서 $x_1, x_2$와 $y$사이에 층을 하나 더 쌓게 되면 XOR 연산을 표현할 수 있게 된다. 이렇게 층이 하나씩 더 쌓일 때 마다 복잡한 회로를 만들 수 있게 되면서 다양한 논리 연산이 가능해진다.