[인공지능 이론] Manifold Learning
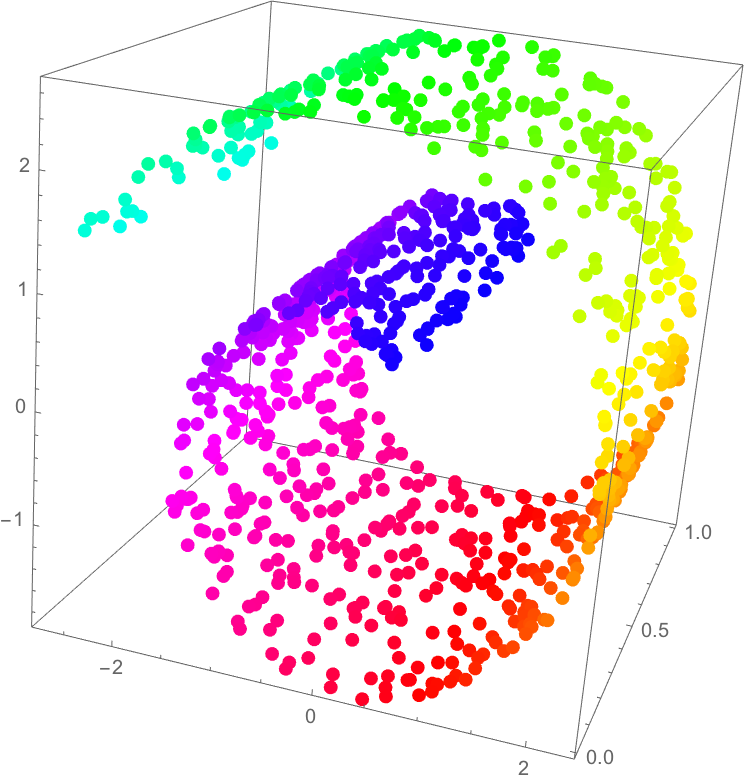
Manifold Learning이란 고차원 데이터가 있을 때 고차원 데이터를 데이터 공간에 뿌리면 샘플들을 잘 아우르는 subspace가 있을 것이라 가정에서 학습을 진행하는 방법이다. Manifold Learning은 차원축소를 위해 사용하며 이를 통해 고차원 데이터를 저차원에서도 잘 표현하는 공간인 manifold를 찾아 차원을 축소시킨다.
이러한 차원축소가 필요한 이유는 크게 두 가지로, 첫 번째는 차원의 저주 문제를 해결하기 위함이다. 고차원으로 갈수록 데이터들은 희박하게 분포하게 된다. 이럴 경우 비슷한 데이터들의 특성을 잘 표현할 수 없다. 따라서 차원축소로 차원의 저주 문제를 해결하고, 학습 속도와 모델 성능을 향상시키기 위해 Manifold Learning이 사용된다.
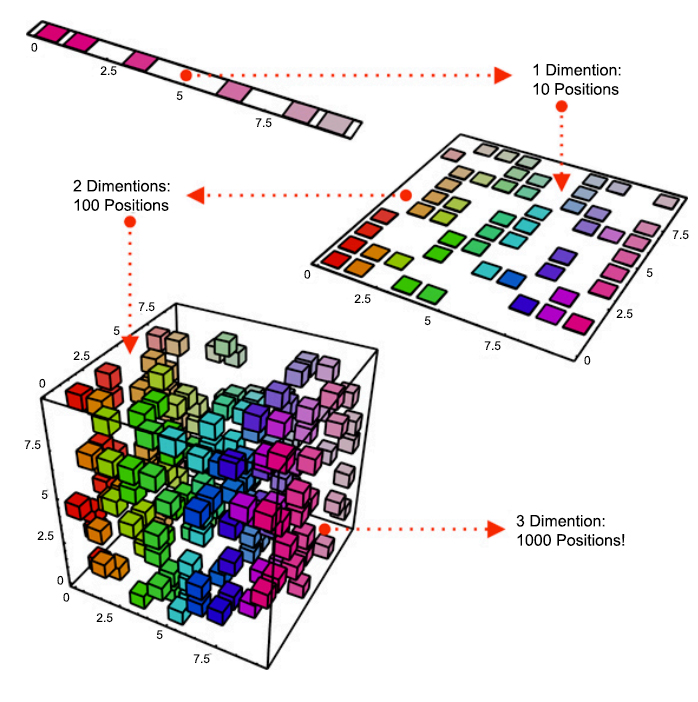
두 번째는 아래 그림과 같이 고차원 공간상에서의 데이터 포인트가 의미적으로 가까워보일 수 있으나 실제로는 거리가 먼 경우가 있고, 의미적으로 완전히 다를 수 있기 때문이다. 앞서 언급한 차원의 저주로 인해서 고차원 상에서 유의미한 거리 측정하기가 매우 어렵다.

이러한 문제를 해결하고자 Manifold Learning 즉, 차원축소 방법이 필요하다. 이러한 차원축소 방법 종류는 아래와 같이 크게 선형과 비선형으로 나뉘며 선형에는 PCA, LDA가 비선형에는 t-SNE, LLE, ISOMAP, MDS, AE 등이 있다.
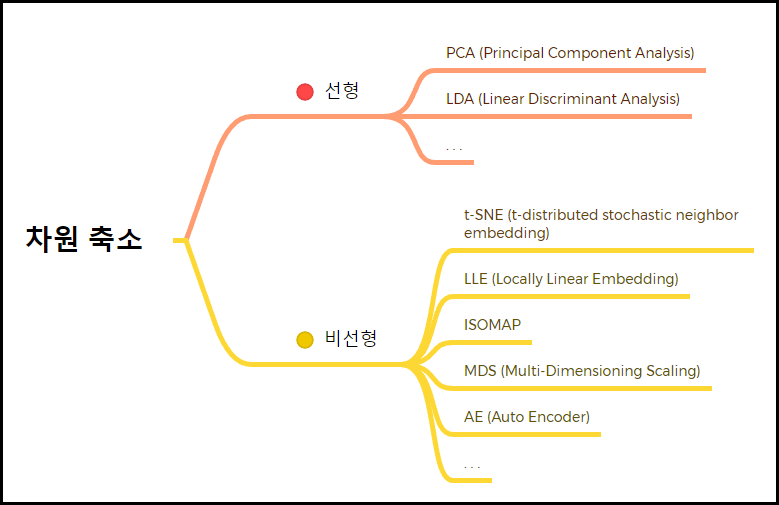
선형
PCA는 1993년에 만들어진 차원축소 기법으로, 데이터를 투영시켰을 때 분산을 가장 크게 만드는 어떤 벡터(Principal Axis)를 찾는 방식으로 동작한다. 이를 위해 공분산 행렬과 특이값 분해(SVD)를 사용한다.(https://roytravel.tistory.com/341)
LDA는 선형판별분석이라 부르며 다른 클래스에 속한 데이터를 선형 분류 가능하도록 데이터 포인트를 투영시키는 알고리즘이다. PCA는 단순히 데이터 포인트의 분산이 가장 크도록 만드는 벡터를 찾았다. 반면 LDA는 데이터 포인트를 투영시켰을 때, 클래스간 거리를 최대가 될 수 있게 데이터 포인트의 평균거리 합을 최대로 만드는 조건과 클래스 내 데이터 포인트의 분산을 최소로 만드는 조건을 갖춘 벡터를 찾는다.
비선형
t-SNE는 고차원 공간에서 유사한 두 벡터가 저차원에서도 유사하도록 원 공간에서 점들 간 유사도를 보존하며 차원을 축소하는 방법이다.
Kernel PCA는 기존 PCA와 같이 linear projection을 수행하는 것이 아닌 약간의 트릭을 추가하여 non-linear projection을 수행할 수 있도록 하는 방법이다.
LLE는 PCA로는 불가능한 비선형적 차원 축소를 가능하게 하는 방법이다. 고차원 공간에서 인접한 데이터 포인트 간의 선형적 구조를 보존하면서 저차원으로 임베딩한다. 다르게 말해 LLE는 각 데이터 포인트들이 k개의 neighbor들과 얼마나 선형적으로 연결되어있는가를 추론하는 과정이다. 크게 아래 3단계로 동작한다.

첫 번째로 가장 가까운 이웃을 찾고 두 번째로 가중치 행렬을 구성한 다음 부분적으로 고유치를 분해하는 방식으로 동작한다. LLE는 기본적으로 isomap 방식과 목적은 동일하지만 Locality를 어떻게 수학적으로 반영하냐에 따라 ISOMAP의 차이가 발생한다.
ISOMAP은 1952년에 만들어진 것으로 다차원 스케일링(MDS) 또는 주성분 분석(PCA) 두 방법론을 결합한 방법이다. 모든 점 사이의 측지 거리를 유지하는 더 낮은 차원의 임베딩을 찾는다. 측지 거리란 두 측점 사이의 타원 체면을 따라 이뤄진 거리를 말한다.
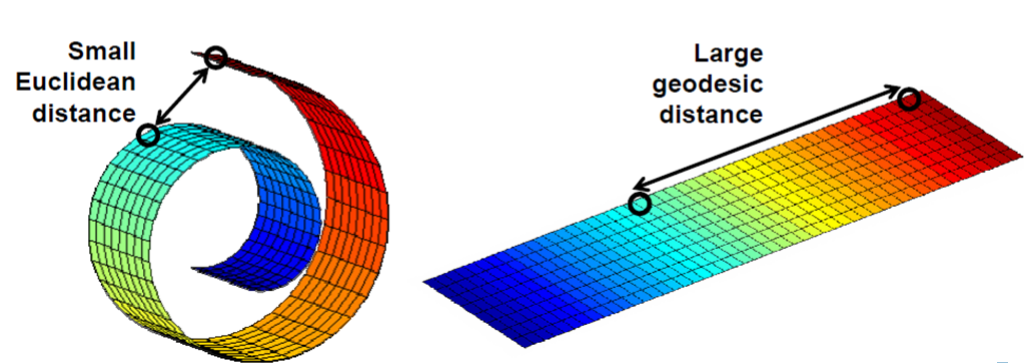
위 그림을 보면 두 점은 유클리디안 거리로는 가깝지만 실제 측지 거리는 색깔이 나타내는 의미만큼 멀리 떨어져 위치함을 알 수 있다. 즉, Isomap 알고리즘은 두 데이터간의 실제 특징을 반영하는 거리 정보를 사용하는 효과적인 차원 축소를 추구한다.
MDS는 다차원척도법으로 D차원 공간 상의 데이터가 있을 때 그 데이터 간의 거리가 저차원 공간상에서도 최대한 보존되도록 하는 벡터를 찾는 방법이다.
Auto Encoder는 실제 공간에 표현된 데이터를 보다 잘 표현할 수 있는 잠재 공간(latent space)를 찾아 축소하는 방법이다. 데이터를 잠재 공간으로 압축하는 encoder와, 잠재공간을 이용해 원래 데이터로 복원시키는 decoder를 사용한다.
Reference